【讲通练透】高考数学知识大盘点 专题05 一元函数的导数及其应用（思维导图 知识梳理 方法技巧 易混易错）

这是一份【讲通练透】高考数学知识大盘点 专题05 一元函数的导数及其应用（思维导图 知识梳理 方法技巧 易混易错），文件包含专题05一元函数的导数及其应用原卷版docx、专题05一元函数的导数及其应用解析版docx等2份试卷配套教学资源，其中试卷共32页， 欢迎下载使用。
2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。
4、重视错题。错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题05 一元函数的导数及其应用
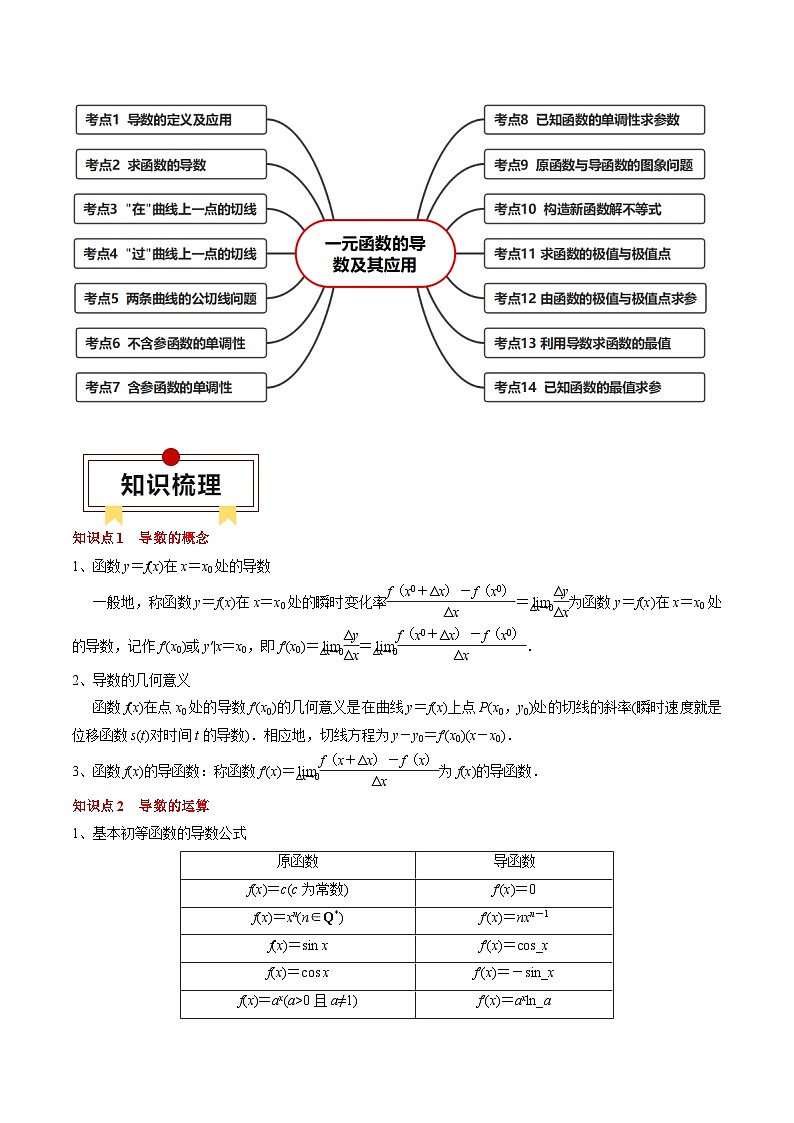
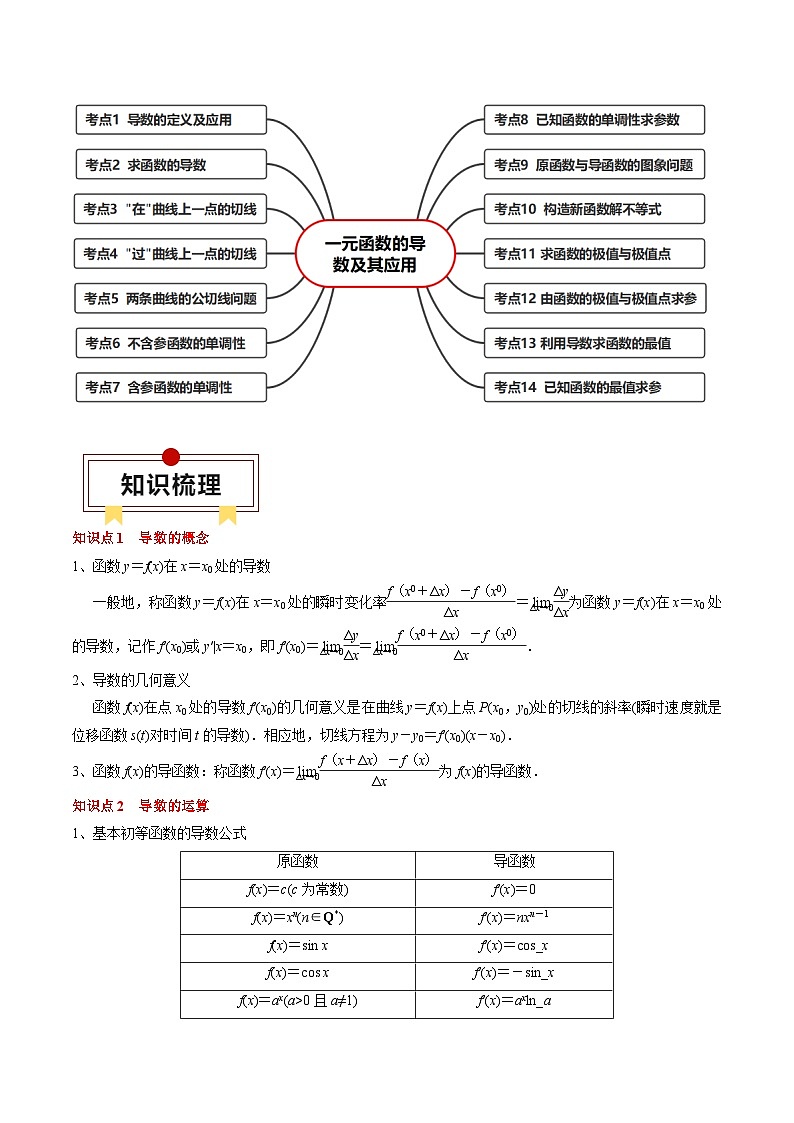
一、知识速览
二、考点速览
知识点1 导数的概念
1、函数y＝f(x)在x＝x0处的导数
一般地，称函数y＝f(x)在x＝x0处的瞬时变化率eq \f(f（x0＋Δx）－f（x0）,Δx)＝eq \(lim,\s\d5(Δx→0))eq^\(lim,\s\d4(Δx→0))eq \f(Δy,Δx)为函数y＝f(x)在x＝x0处的导数，记作f′(x0)或y′|x＝x0，即f′(x0)＝eq \(lim,\s\d5(Δx→0))eq^\(lim,\s\d4(Δx→0))eq \f(Δy,Δx)＝eq^\(lim,\s\d4(Δx→0))eq \(lim,\s\d5(Δx→0))eq \f(f（x0＋Δx）－f（x0）,Δx)．
2、导数的几何意义
函数f(x)在点x0处的导数f′(x0)的几何意义是在曲线y＝f(x)上点P(x0，y0)处的切线的斜率(瞬时速度就是位移函数s(t)对时间t的导数)．相应地，切线方程为y－y0＝f′(x0)(x－x0)．
3、函数f(x)的导函数：称函数f′(x)＝eq^\(lim,\s\d4(Δx→0))eq \(lim,\s\d5(Δx→0))eq \f(f（x＋Δx）－f（x）,Δx)为f(x)的导函数．
知识点2 导数的运算
1、基本初等函数的导数公式
2、导数的运算法则
(1)[f(x)±g(x)]′＝f′(x)±g′(x)．
(2)[f(x)·g(x)]′＝f′(x)g(x)＋f(x)g′(x)．
(3)eq \b\lc\[\rc\](\a\vs4\al\c1(\f(f（x）,g（x）)))′＝eq \f(f′（x）g（x）－f（x）g′（x）,[g（x）]2)(g(x)≠0)．
知识点3 利用导数研究函数的单调性
1、导数与函数的单调性的关系
在某个区间内，如果，那么函数在这个区间内单调递增；
如果，那么函数在这个区间内单调递减．
【注意】
（1）在某区间内（）是函数在此区间上为增（减）函数的充分不必要条件；
（2）可导函数在上是增(减)函数的充要条件是对∀x∈(a，b)，都有（）且在上的任何子区间内都不恒为零．
2、导数法求函数单调区间的步骤
（1）确定函数的定义域；
（2）求（通分合并、因式分解）；
（3）解不等式，解集在定义域内的部分为单调递增区间；
（4）解不等式，解集在定义域内的部分为单调递减区间．
知识点4 导数与函数的极值、最值
1、函数的极值
（1）函数的极小值：函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．
（2）函数的极大值：函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．
2、函数的最值
（1）在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．
（2）若函数f(x)在[a，b]上单调递增，则f(a)为函数的最小值，f(b)为函数的最大值；若函数f(x)在[a，b]上单调递减，则f(a)为函数的最大值，f(b)为函数的最小值．
一、求曲线“在”与“过”某点的切线
1、求曲线“在”某点处的切线方程步骤
第一步（求斜率）：求出曲线在点处切线的斜率
第二步（写方程）：用点斜式
第三步（变形式）：将点斜式变成一般式。
2、求曲线“过”某点处的切线方程步骤
第一步：设切点为；
第二步：求出函数在点处的导数；
第三步：利用Q在曲线上和，解出及；
第四步：根据直线的点斜式方程，得切线方程为．
【典例1】（2023·陕西西安·西安市大明宫中学校考模拟预测）已知函数，则曲线在点处的切线方程为（ ）
A． B． C． D．
【答案】B
【解析】，切点为，，
所以切线方程为，即故选：B
【典例2】（2023·西藏日喀则·统考一模）已知直线是曲线在点处的切线方程，则
【答案】e
【解析】由题设，且，则，
所以，切线方程为，即，
所以，故.
【典例3】（2023·云南·校联考模拟预测）曲线过坐标原点的切线方程为 .
【答案】
【解析】设切点为，则，
，切线的斜率为，
所以切线方程为，
又切线过原点，所以，即，
解得，所以切线方程为
【典例4】（2023·陕西宝鸡·统考二模）若过点可作曲线的三条切线，则的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】设切点为，
由函数，可得，则
所以在点处的切线方程为，
因为切线过点，所以，
整理得，
设，所以，
令，解得或，令，解得，
所以在上单调递增，在上单调递减，在上单调递增，
要使得过点可作曲线的三条切线，
则满足，解得，即的取值范围是．故选：C．
二、含参函数单调性讨论依据
（1）导函数有无零点讨论（或零点有无意义）；
（2）导函数的零点在不在定义域或区间内；
（3）导函数多个零点时大小的讨论。
【典例1】（2023·全国·高三对口高考）已知函数，求函数的单调区间．
【答案】答案见解析.
【解析】函数的定义域为，求导得，
当时，，由，得，由，得，
因此函数在上单调递增，在上单调递减；
当时，由，得或，
当或时，，当时，，
因此在，上单调递增，在上单调递减；
当时，恒成立，当且仅当时取等号，因此在上单调递增；
当时，当或时，，当时，，
因此在，上单调递增，在上单调递减，
所以当时，的单调递增区间为，单调递减区间为；
当时，的单调递增区间为，，单调递减区间为；
当时，的单调递增区间为，无单调递减区间；
当时，的单调递增区间为，，单调递减区间为.
【典例2】（2023·全国·高三专题练习）讨论函数的单调性．
【答案】答案见解析
【解析】函数的定义域为，
求导得，
令，得，其中.
当时，，故在上单调递增；
当时，，则，故在上单调递增；
当时，，由得，，
所以或时，；时，，
所以在，上单调递增，在上单调递减．
综上所述，当时，在上单调递增；
当时，在，上单调递增，
在上单调递减．
三、已知函数的单调性求参数
（1）函数在区间D上单调增（单减）在区间D上恒成立；
（2）函数在区间D上存在单调增（单减）区间在区间D上能成立；
（3）已知函数在区间D内单调不存在变号零点
（4）已知函数在区间D内不单调存在变号零点
【典例1】（2023·全国·高三专题练习）已知函数在区间上单调递增，则a的最小值为（ ）．
A． B．e C． D．
【答案】C
【解析】依题可知，在上恒成立，显然，所以，
设，所以，所以在上单调递增，
，故，即，即a的最小值为．故选：C．
【典例2】（2023·全国·高三专题练习）已知函数在上不单调，则的取值范围是（ ）
A． B． C． D．
【答案】A
【解析】依题意，故在上有零点，
令，令，得，
令，则，
由，得，单调递增，又由，得，
故，所以，的取值范围故选：A
【典例3】（2023·全国·高三专题练习）若函数恰有三个单调区间，则实数a的取值范围为（ ）
A． B． C． D．
【答案】C
【解析】由题意得函数的定义域为，，
要使函数恰有三个单调区间，
则有两个不相等的实数根，∴，解得且，
故实数a的取值范围为，故选：C.
四、构造函数法解决函数问题中的常见类型
关系式为“加”型构造：
构造
（2） 构造
（3） 构造
（4）构造（注意的符号）
（5） 构造
关系式为“减”型构造：
（6） 构造
（7） 构造
（8） 构造
（9）构造（注意的符号）
（10） 构造
【典例1】（2023春·重庆·高二校联考期中）已知定义在上的函数满足：，且，则的解集为（ ）
A． B． C． D．
【答案】A
【解析】设，，
因为，所以，所以在单调递增，
因为，所以，
由，且得，则，
所以，又在单调递增，所以，故选：A．
【典例2】（2023春·江西南昌·高二校联考阶段练习）若定义域为的函数满足，则不等式的解集为 .
【答案】
【解析】由时，函数满足，可得，
设，则，故在上单调递增，
由，即，即，
所以，解得，所以的解集为.
【典例3】（2023春·四川宜宾·高二校考期中）已知是定义在上的函数，导函数满足对于恒成立，则（ ）
A．， B．，
C．， D．，
【答案】D
【解析】设函数，由，可得，
所以在R上单调递减，
则，得，即，
则，得，即.故选：D
五、单变量不等式恒成立问题
一般利用参变分离法求解函数不等式恒（能）成立，可根据以下原则进行求解：
1、，
2、，
3、，
4、，
【典例1】（2023·全国·高三专题练习）若对于，不等式恒成立，则参数a的取值范围为 ．
【答案】
【解析】令，可得，
若时，，单调递减，
又由，所以当时，可得，不符合题意，舍去；
若时，令，可得，
当时，，单调递减；
当时，，单调递增；
又由，所以存在，使得，不符合题意，舍去；
若时，令，可得，
当时，，单调递增，且，
所以当时，恒成立，符合题意，
所以实数的取值范围为．
【典例2】（2023·全国·高三专题练习）已知函数，若对任意的，恒成立，求实数的取值范围．
【答案】
【解析】解法一，由在上恒成立，得在上恒成立，
即在上恒成立
令，，则．
当时，，当时，，
所以在上单调递增，在上单调递减，所以
因为，，所以，
所以，即实数的取值范围为．
解法二，由在上恒成立，得在上恒成立．
令，，则满足即可
，当时，，当时，，
所以在上单调递减，在上单调递增，所以．
因为，，所以，
所以，即实数的取值范围为．
六、双变量不等式与等式
一般地，已知函数，
1、不等关系
（1）若，，总有成立，故；
（2）若，，有成立，故；
（3）若，，有成立，故；
（4）若，，有成立，故．
2、相等关系
记的值域为A, 的值域为B,
（1）若，，有成立，则有；
（2）若，，有成立，则有；
（3）若，，有成立，故；
一般利用参变分离法求解函数不等式恒（能）成立，可根据以下原则进行求解：
1、，
2、，
3、，
4、，
【典例1】（2023春·四川宜宾·高二校考期中）已知函数，，对任意的，都有成立，则实数的取值范围是（ ）
A． B． C． D．
【答案】A
【解析】，则，
令，解得或；令， 解得，
，故在单调递减，在单调递增，在单调递减，
且，故，
任意的，都有成立，则，
因为，则，
当时，在单调递增，
所以，
故，即(舍去)；
当时，令，解得；令， 解得，
故在上单调递减， 在上单调递增，
所以，
所以，即， 解得，
综上所述，实数的取值范围为.故选：A
【典例2】（2023·全国·高三专题练习）已知函数，函数，若对任意的，存在，使得，则实数m的取值范围为 ．
【答案】
【解析】由题意得．
因为，
当时，，故在上单调递增，．
因为，
当时，，当时，，
故在上单调递增，在上单调递减，．
由，即，解得．
易错点1 复合函数求导错误
点拨：复合函数对自变量的导数等于已知函数对中间变量的导数，乘以中间变量对自变量的导数，即。
【典例1】（2023·全国·高三专题练习）求下列函数的导数．
(1)； (2)； (3) (4)；
【答案】(1)；(2)；(3)；(4)
【解析】（1）因为，所以.
（2）因为，所以.
（3）因为，所以
（4）因为，所以
【典例2】（2023·全国·高三专题练习）求的导函数.
【答案】
【解析】因为，
所以.
故答案为：
易错点2 误解“导数为0”与“有极值”的逻辑关系
点拨：在使用导数求函数极值时，很容易出现的错误是求出使导函数等于0的点，而没有对这些点左右两侧导函数的符号进行判断，误以为使导函数等于0的点就是函数的极值点。出现这种错误的原因就是对导数与极值关系不清。可导函数在一点处的导函数值为0只是这个函数在此点取到极值的必要条件，充要条件是两侧异号。
【典例1】（2022秋·辽宁鞍山·高三校联考期中）已知定义域为的函数的导函数为，且函数的部分图象如图所示，则下列说法中正确的是（ ）
A．有极小值，极大值 B．有极小值，极大值
C．有极小值，极大值和 D．有极小值，极大值
【答案】D
【解析】观察图象知，当时，或且，
当时，或，
而当时，，当时，，
因此当或时，，
当时，，当且仅当时取等号，
则在上单调递减，在上单调递增，
所以有极小值，极大值，A，B，C不正确；D正确.故选：D
【典例2】（2022秋·北京·高三北京铁路二中校考阶段练习）设函数的定义域为，是的极大值点，以下四个结论中正确的命题序号是 .
①，； ②是的极大值点；
③是的极小值点； ④是的极小值点
【答案】②④
【解析】对于①：是的极大值点，并不一定是最大值点，即①错误；
对于②：因为与的图象关于轴对称，
且是的极大值点，
所以应是的极大值点，即②正确；
对于③：因为与的图象关于轴对称，
且是的极大值点，
所以应是的极小值点，
且无法判定是的极小值点，即③错误；
对于④：因为与的图象关于对称，
且是的极大值点，
所以应是的极小值点，即④正确；故答案为：②④.
【典例3】（2023·全国·高三对口高考）如果函数在处有极值，则的值为 ．
【答案】2
【解析】因为函数在处有极值，
所以，.
由于，
所以，，
解得：或.
当时，，
，所以单调递减，无极值.
所以.故答案为：2
易错点3 对“导数值符号”与“函数单调性”关系理解不透彻
点拨：一个函数在某个区间上单调增（减）的充要条件是这个函数的导函数在此区间上恒大（小）于等于0，且导函数在此区间的任意子区间上都不恒为0。切记导函数在某区间上恒大（小）于0仅为该函数在此区间上单调增（减）的充分条件。
【典例1】（2023·陕西西安·统考三模）若函数在区间上单调递增，则的取值范围是（ ）
A． B． C． D．
【答案】B
【解析】因为函数在区间上单调递增，
所以在区间上恒成立，即在区间上恒成立，
令，则，
所以在上递增，又，所以.
所以的取值范围是.故选：B
【典例2】（2022秋·山东济宁·高三校考阶段练习）已知函数，若在内为减函数，则实数a的取值范围是 ．
【答案】
【解析】，
∵在内为减函数，
∴在内恒成立，
∴，即，解得．
所以实数a的取值范围是．
【典例3】（2023·全国·高三专题练习）已知函数的单调递减区间为，则的值为（ ）
A．3 B． C．6 D．
【答案】D
【解析】由，所以，
单调递减区间是，的解集为，
即的解集为，
，，经检验符合题意.故选：D.
易错点4 对“导函数值正负”与“原函数图象升降”关系不清楚
点拨：解答此类题的关键是抓住①导函数的零点与原函数的极值点关系——极值点的导数值为0；②导函数值的符号与原函数单调性的关系——原函数看增减，导函数看正负。
【典例1】（2023·浙江绍兴·统考模拟预测）如图是函数的导函数的图象，若，则的图象大致为（ ）
A． B． C． D．
【答案】D
【解析】由的图象可知，当时，，
则在区间上，函数上各点处切线的斜率在区间内，
对于A，在区间上，函数上各点处切线的斜率均小于0，故A不正确；
对于B，在区间上，函数上存在点，在该点处切线的斜率大于1，故B不正确；
对于C，在区间上，函数上存在点，在该点处切线的斜率大于1，故C不正确；
对于D，由的图象可知，当时，，
当时，，当时，，
所以函数上各点处切线的斜率在区间内，在上单调递增，
在上单调递减，在上单调递增，
而函数的图象均符合这些性质，故D正确.故选：D
【典例2】（2023·全国·高三专题练习）（多选）已知定义在上的函数，其导函数的大致图像如图所示，则下列叙述正确的是（ ）
A． B．
C． D．
【答案】CD
【解析】由题意得，当时，，所以函数在上单调递增，
因为，所以，C选项正确.
当时，，所以函数在上单调递减，
因为，所以，D选项正确.故选：CD原函数
导函数
f(x)＝c(c为常数)
f′(x)＝0
f(x)＝xn(n∈Q*)
f′(x)＝nxn－1
f(x)＝sin x
f′(x)＝cs_x
f(x)＝cs x
f′(x)＝－sin_x
f(x)＝ax(a>0且a≠1)
f′(x)＝axln_a
f(x)＝ex
f′(x)＝ex
f(x)＝lgax(x>0，a>0且a≠1)
f′(x)＝eq \f(1,xln a)
f(x)＝ln x (x>0)
f′(x)＝eq \f(1,x)