【讲通练透】高考数学知识大盘点 专题07 三角函数的图象与性质综合（思维导图 知识梳理 方法技巧 易混易错）

这是一份【讲通练透】高考数学知识大盘点 专题07 三角函数的图象与性质综合（思维导图 知识梳理 方法技巧 易混易错），文件包含专题07三角函数的图象与性质综合原卷版docx、专题07三角函数的图象与性质综合解析版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。
2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。
4、重视错题。错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题07 三角函数的图象与性质综合
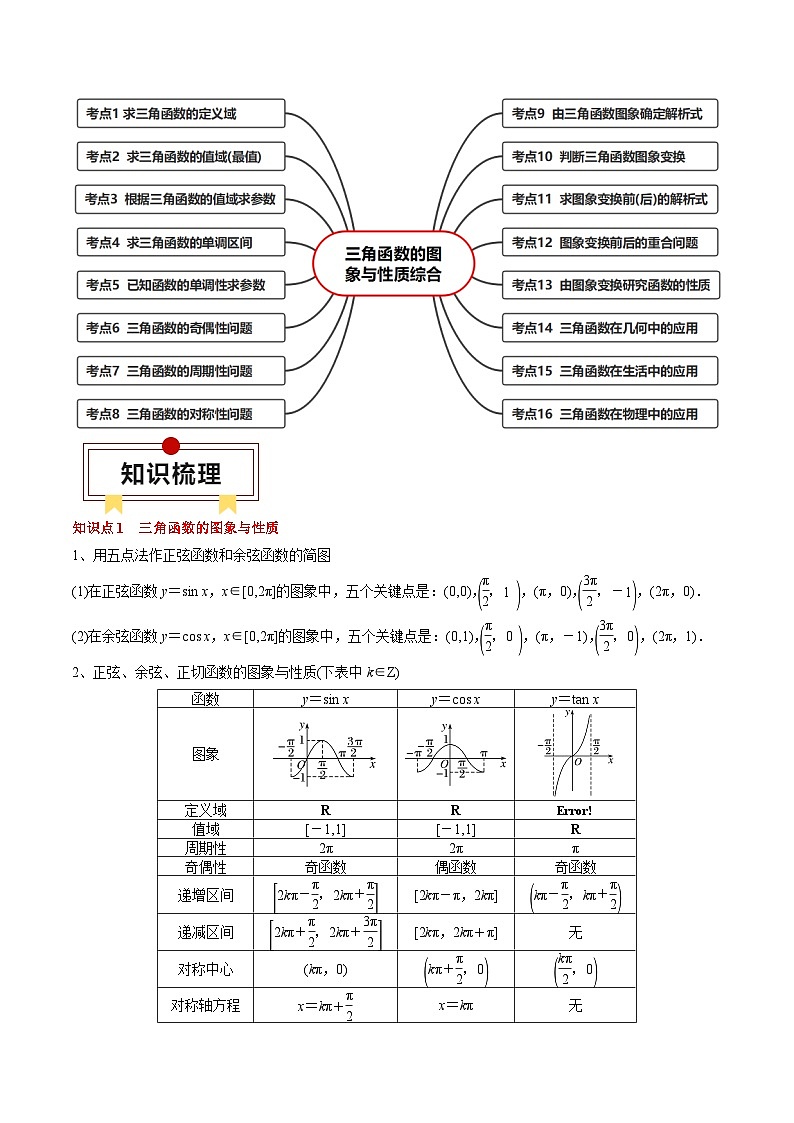
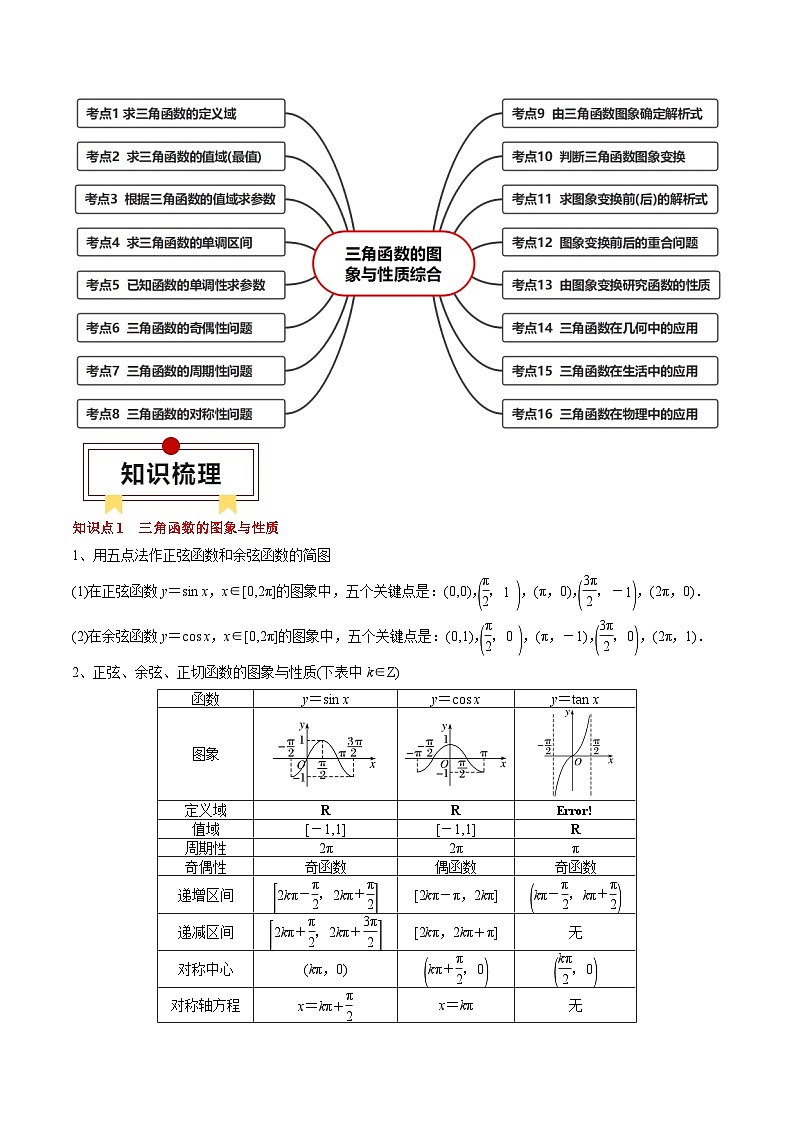
一、知识速览
二、考点速览
知识点1 三角函数的图象与性质
1、用五点法作正弦函数和余弦函数的简图
(1)在正弦函数y＝sin x，x∈[0,2π]的图象中，五个关键点是：(0,0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，1))，(π，0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，－1))，(2π，0)．
(2)在余弦函数y＝cs x，x∈[0,2π]的图象中，五个关键点是：(0,1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，0))，(π，－1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，0))，(2π，1)．
2、正弦、余弦、正切函数的图象与性质(下表中k∈Z)
知识点2 函数Asin(ωx＋φ)
1、y＝Asin(ωx＋φ)的有关概念
2、用五点法画y＝Asin(ωx＋φ)(A>0，ω>0)
知识点3 三角函数图象变换
由函数y＝sin x的图象通过变换得到y＝Asin(ωx＋φ)(A>0，ω>0)的图象的两种方法
一、三角函数定义域的求法
求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数图象来求解．
【注意】解三角不等式时要注意周期，且k∈Z不可以忽略．
【典例1】（2022·全国·高三专题练习）函数的定义域为（ ）
A． B．且 C． D．或
【典例2】（2023·全国·高三专题练习）函数的定义域为 ．
【典例3】（2022·全国·高三专题练习）函数定义域为（ ）
A． B．
C． D．
二、三角函数值域或最值的3种求法
1、直接法：形如y＝asin x＋k或y＝acs x＋k的三角函数，直接利用sin x，cs x的值域求出；
2、化一法：形如y＝asin x＋bcs x＋k的三角函数，化为y＝Asin(ωx＋φ)＋k的形式，确定ωx＋φ的范围，根据正弦函数单调性写出函数的值域(最值)；
3、换元法：
（1）形如y＝asin2x＋bsin x＋k的三角函数，可先设sin x＝t，化为关于t的二次函数求值域(最值)；
（2）形如y＝asin xcs x＋b(sin x±cs x)＋c的三角函数，可先设t＝sin x±cs x，化为关于t的二次函数求值域(最值)
【典例1】（2023·全国·高三对口高考）的最小值为 .
【典例2】（2022秋·江西·高三校联考阶段练习）函数在区间上的最小值是 .
【典例3】（2022秋·重庆·高三重庆一中校考）函数的最小值是 ．
【典例4】（2022·全国·高三专题练习）函数，的值域为 ．
三、求三角函数单调区间的2种方法
1、代换法：就是将比较复杂的三角函数含自变量的代数式整体当作一个角u(或t)，利用基本三角函数的单调性列不等式求解；
2、图象法：画出三角函数的正、余弦和正切曲线，结合图象求它的单调区间
求解三角函数的单调区间时，若x的系数为负，应先化为正，同时切莫忽视函数自身的定义域．
【典例1】（2023·全国·模拟预测）将函数的图象上各点向右平移个单位长度得函数的图象，则的单调递增区间为（ ）
A． B．
C． D．
【典例2】（2023·吉林·梅河口市第五中学校考模拟预测）下列区间中，函数单调递减的区间是（ ）
A． B． C． D．
【典例3】（2023·全国·高三专题练习）函数的单调递增区间为（ ）
A．， B．，
C． ， D． ，
四、已知单调区间求参数范围的3种方法
1、子集法：求出原函数的相应单调区间，由已知区间是所求某区间的子集，列不等式(组)求解；
2、反子集法：由所给区间求出整体角的范围，由该范围是某相应正、余弦函数的某个单调区间的子集，列不等式(组)求解；
3、周期性法：由所给区间的两个端点到其相应对称中心的距离不超过eq \f(1,4)周期列不等式(组)求解。
【典例1】（2023秋·重庆·高三统考开学考试）已知函数在区间上是单调的，则的取值范围是（ ）
A． B． C． D．
【典例2】（2023·山东烟台·统考二模）已知函数在上单调递增，则的取值范围为（ ）．
A． B． C． D．
【典例3】（2022·全国·高三专题练习）已知函数 在内是减函数， 则（ ）
A． B． C． D．
五、与三角函数奇偶性相关的结论
三角函数中，判断奇偶性的前提是定义域关于原点对称，奇函数一般可化为y＝Asin ωx或y＝Atan ωx的形式，而偶函数一般可化为y＝Acs ωx＋b的形式．常见的结论有：
（1）若y＝Asin(ωx＋φ)为偶函数，则有φ＝kπ＋eq \f(π,2)(k∈Z)；若为奇函数，则有φ＝kπ(k∈Z)．
（2）若y＝Acs(ωx＋φ)为偶函数，则有φ＝kπ(k∈Z)；若为奇函数，则有φ＝kπ＋eq \f(π,2)(k∈Z)．
（3）若y＝Atan(ωx＋φ)为奇函数，则有φ＝kπ(k∈Z)．
【典例1】（2023·河北沧州·校考模拟预测）若函数为奇函数，则的最小值为 .
【典例2】（2022秋·重庆·高三重庆实验中学校考期中）已知函数是偶函数，则的值为（ ）
A． B．1 C．1或-1 D．
【典例3】（2022秋·河南·高三郑州外国语学校校考）已知，则“函数的图象关于轴对称”是“”的（ ）
A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件
六、三角函数对称性问题的2种求解方法
1、定义法：正(余)弦函数的对称轴是过函数的最高点或最低点且垂直于x轴的直线，对称中心是图象与x轴的交点，即函数的零点；
2、公式法：
（1）函数y＝Asin(ωx＋φ)的对称轴为x＝eq \f(kπ,ω)－eq \f(φ,ω)＋eq \f(π,2ω)，对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,ω)－\f(φ,ω)，0))；
（2）函数y＝Acs(ωx＋φ)的对称轴为x＝eq \f(kπ,ω)－eq \f(φ,ω)，对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,ω)－\f(φ,ω)＋\f(π,2ω)，0))；
（3）函数y＝Atan(ωx＋φ)的对称中心为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2ω)－\f(φ,ω)，0)).上述k∈Z
【典例1】（2023秋·重庆·高三万州第二高级中学校考）函数图象的对称轴是（ ）
A． B． C． D．
【典例2】（2023·陕西安康·统考一模）设函数的图象的一个对称中心为，则的一个最小正周期是（ ）
A． B． C． D．
【典例3】（2023·河南开封·校考模拟预测）已知函数的图象关于点对称，那么的最小值为 ．
七、三角函数图象的变换
函数y＝Asin(ωx＋φ)＋k(A>0，ω>0)中，参数A，ω，φ，k的变化引起图象的变换：
（1）A的变化引起图象中振幅的变换，即纵向伸缩变换；
（2）ω的变化引起周期的变换，即横向伸缩变换；
（3）φ的变化引起左右平移变换，k的变化引起上下平移变换．
图象平移遵循的规律为：“左加右减，上加下减”．
【注意】（1）平移变换和伸缩变换都是针对x而言，即x本身加减多少值，而不是依赖于ωx加减多少值；
（2）余弦型、正切型函数的图象变换过程与正弦型函数的图象变换过程相同。
【典例1】（2023·四川南充·统考三模）已知点是函数的一个对称中心，则为了得到函数的图像，可以将图像（ ）
A．向右平移个单位，再向上移动1个单位 B．向左平移个单位，再向上移动1个单位
C．向右平移个单位，再向下移动1个单位 D．向右平移个单位，再向下移动1个单位
【典例2】（2023·西藏林芝·校考模拟预测）为了得到函数的图象，只需将函数的图象（ ）
A．向左平移个单位长度 B．向右平移个单位长度
C．向左平移个单位长度 D．向右平移个单位长度
易错点1 忽视正、余弦函数的有界性
点拨：许多三角函数问题可以通过换元的方法转化为代数问题解决，在换元时注意正、余弦函数的有界性．
【典例1】（2022·全国·高三专题练习）函数y＝cs2x－sin x的值域是
【典例2】（2023春·河丘·高三临颍县第一高级中学校联考）函数的最小值为（ ）
A． B．0 C．2 D．6
【典例3】（2023·全国·高三专题练习）设，则的最小值为 .
【典例4】（2023·全国·高三专题练习）求函数的值域．
易错点2 三角函数单调性判断错误
点拨：对于函数来说，当时，由于内层函数是单调递增的，所以函数的单调性与函数的单调性相同，故可完全按照函数的单调性来解决；但当时，内层函数是单调递减的，所以函数的单调性与函数的单调性正好相反，就不能按照函数的单调性来解决。一般来说，应根据诱导公式将的系数化为正数加以解决，对于带有绝对值的三角函数宜根据图象从直观上加以解决。
【典例1】（2023·全国·高三专题练习）函数的单调递减区间是（ ）
A． B．
C． D．
【典例2】（2023·河南·校联考模拟预测）已知函数，，则的单调递增区间是（ ）
A． B． C．， D．，
易错点3 图象变换的方向把握不准
点拨：图像的平移变换，伸缩变换因先后顺序不同平移的量不同，平移的量为，平移的量为。
【典例1】（2023春·重庆·高三重庆巴蜀中学校考）函数的图象经过下列哪个变换可以得到的图象，这个变换是（ ）
A．先将函数的图象向左平移个单位，再把图象上每个点的横坐标扩大为原来的2倍
B．先将函数的图象向左平移个单位，再把图象上每个点的横坐标缩小为原来的
C．先把函数的图象上每个点的横坐标缩小为原来的，再将图象向左平移个单位
D．先把函数的图象上每个点的横坐标扩大为原来的2倍，再将图象向左平移个单位
【典例2】（2023·河北唐山·统考三模）（多选）为了得到函数的图象，只需把余弦曲线上所有的点（ ）
A．横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移
B．横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移
C．向右平移，再把得到的曲线上各点横坐标缩短到原来的倍，纵坐标不变
D．向右平移，再把得到的曲线上各点横坐标缩短到原来的倍，纵坐标不变
【典例3】（2023春·广西·高三鹿寨县鹿寨中学校联考）已知函数的部分图象如下所示，其中，为了得到的图象，需将（ ）
A．函数的图象的横坐标伸长为原来的倍后，再向左平移个单位长度
B．函数的图象的横坐标缩短为原来的后，再向右平移个单位长度
C．函数的图象向左平移个单位长度后，再将横坐标伸长为原来的倍
D．函数的图象向右平移个单位长度后，再将横坐标伸长为原来的倍
易错点4 用零点确定的,忽略图象的升降
点拨：确定φ值时,往往以寻找“五点法”中的特殊点作为突破口．具体如下：“第一点”(即图象上升时与x轴的交点)为ωx＋φ＝0；“第二点”(即图象的“峰点”)为ωx＋φ＝eq \f(π,2)；“第三点”(即图象下降时与x轴的交点)为ωx＋φ＝π；“第四点”(即图象的“谷点”)为ωx＋φ＝eq \f(3π,2)；“第五点”为ωx＋φ＝2π.
【典例1】（2023秋·广东深圳·高三开学校联考）已知函数的图象大致如图，则（ ）

A． B． C． D．1
【典例2】（2023春·陕西安康·高三安康中学校考）已知函数的部分图象如图所示，则（ ）

A． B．
C． D．函数
y＝sin x
y＝cs x
y＝tan x
图象
定义域
R
R
eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(x≠kπ＋\f(π,2)))))
值域
[－1,1]
[－1,1]
R
周期性
2π
2π
π
奇偶性
奇函数
偶函数
奇函数
递增区间
eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ－\f(π,2)，2kπ＋\f(π,2)))
[2kπ－π，2kπ]
eq \b\lc\(\rc\) (\a\vs4\al\c1(kπ－\f(π,2)，kπ＋\f(π,2)))
递减区间
eq \b\lc\[\rc\](\a\vs4\al\c1(2kπ＋\f(π,2)，2kπ＋\f(3π,2)))
[2kπ，2kπ＋π]
无
对称中心
(kπ，0)
eq \b\lc\(\rc\)(\a\vs4\al\c1(kπ＋\f(π,2)，0))
eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(kπ,2)，0))
对称轴方程
x＝kπ＋eq \f(π,2)
x＝kπ
无
y＝Asin(ωx＋φ)
振幅
周期
频率
相位
初相
(A>0，ω>0)
A
T＝eq \f(2π,ω)
f＝eq \f(1,T)＝eq \f(ω,2π)
ωx＋φ
eq \a\vs4\al(φ)
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
x
－eq \f(φ,ω)
eq \f(π,2ω)－eq \f(φ,ω)
eq \f(π－φ,ω)
eq \f(3π,2ω)－eq \f(φ,ω)
eq \f(2π－φ,ω)
y＝Asin(ωx＋φ)
0
eq \a\vs4\al(A)
0
－A
0