【讲通练透】高考数学知识大盘点 专题09 平面向量及其应用（思维导图 知识梳理 方法技巧 易混易错）

这是一份【讲通练透】高考数学知识大盘点 专题09 平面向量及其应用（思维导图 知识梳理 方法技巧 易混易错），文件包含专题09平面向量及其应用原卷版docx、专题09平面向量及其应用解析版docx等2份试卷配套教学资源，其中试卷共42页， 欢迎下载使用。
2、精练习题。复习时不要搞“题海战术”，应在老师的指导下，选一些源于课本的变式题，或体现基本概念、基本方法的基本题，通过解题来提高思维能力和解题技巧，加深对所学知识的深入理解。在解题时，要独立思考，一题多思，一题多解，反复玩味，悟出道理。
3、加强审题的规范性。每每大考过后，总有同学抱怨没考好，纠其原因是考试时没有注意审题。审题决定了成功与否，不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系，确定解题思路 。
4、重视错题。错误是最好的老师”，但更重要的是寻找错因，及时进行总结，三五个字，一两句话都行，言简意赅，切中要害，以利于吸取教训，力求相同的错误不犯第二次。
专题09 平面向量及其应用
一、知识速览
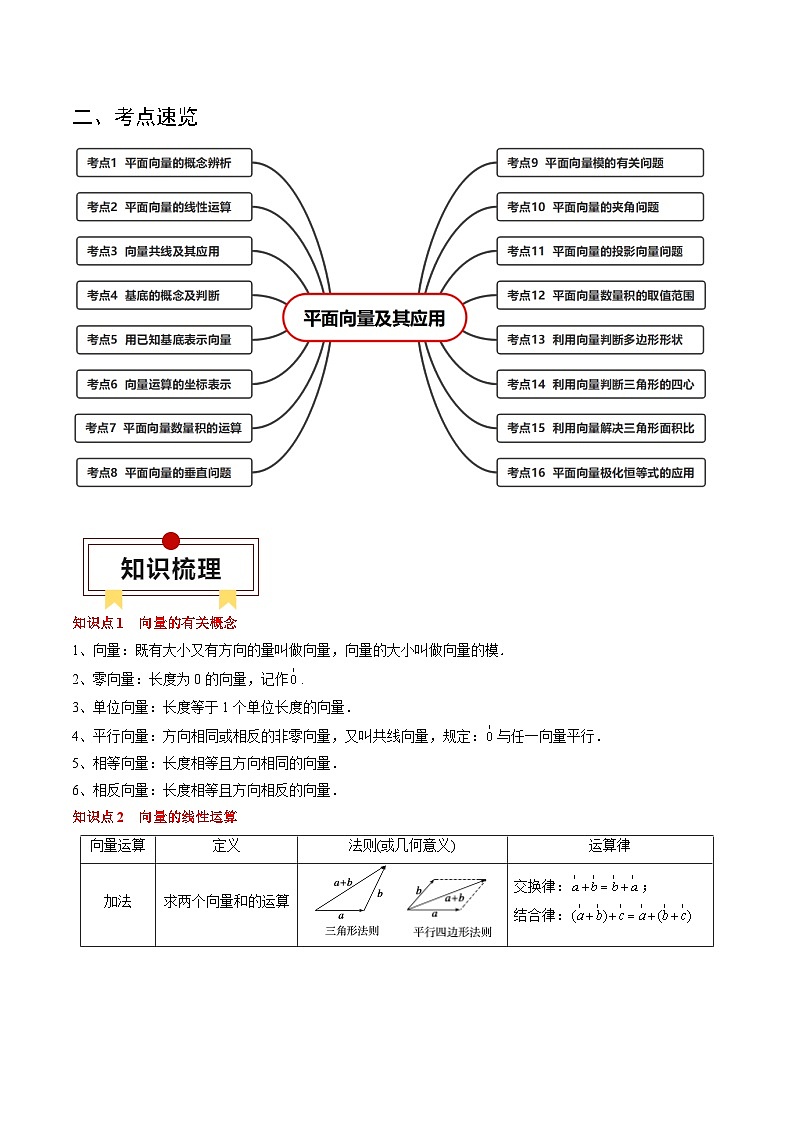
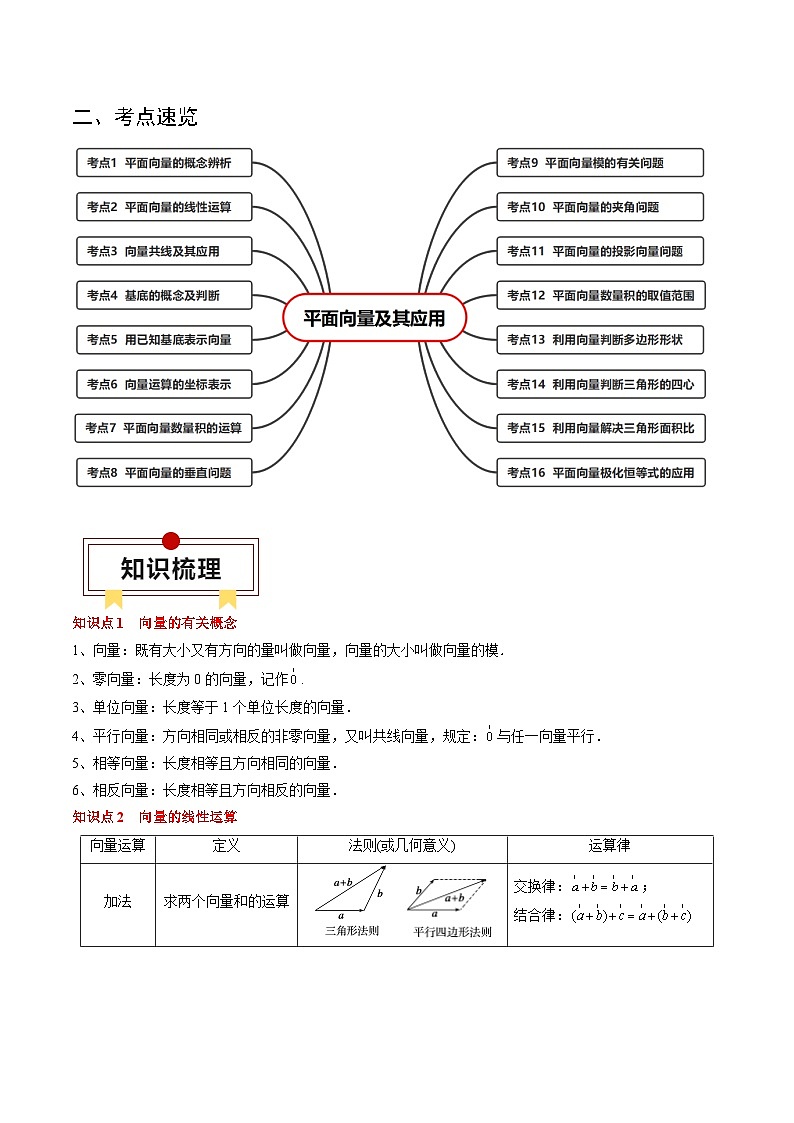
二、考点速览
知识点1 向量的有关概念
1、向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的模．
2、零向量：长度为0的向量，记作.
3、单位向量：长度等于1个单位长度的向量．
4、平行向量：方向相同或相反的非零向量，又叫共线向量，规定：与任一向量平行．
5、相等向量：长度相等且方向相同的向量．
6、相反向量：长度相等且方向相反的向量．
知识点2 向量的线性运算
知识点3 向量共线定理与基本定理
1、向量共线定理：如果，则，反之，如果且，则一定存在唯一的实数，使.
2、三点共线定理：平面内三点、、三点共线的充要条件是：存在实数，使，其中，为平面内一点。
3、平面向量基本定理
（1）定义：如果是同一平面内的两个不共线向量，那么对于这一平面内的任一向量，有且只有一对实数，使
（2）基底：若不共线，我们把叫做表示这一平面内所有向量的一个基底．
（3）对平面向量基本定理的理解
= 1 \* GB3 ①基底不唯一，只要是同一平面内的两个不共线向量都可以作为基底．同一非零向量在不同基底下的分解式是不同的．
= 2 \* GB3 ②基底给定时，分解形式唯一．是被唯一确定的数值．
= 3 \* GB3 ③是同一平面内所有向量的一组基底，
则当与共线时，；当与共线时，；当时，．
= 4 \* GB3 ④由于零向量与任何向量都是共线的，因此零向量不能作为基底中的向量．
知识点4 平面向量的数量积
1、向量的夹角
（1）定义：已知两个非零向量和，作，，则∠AOB就是向量与的夹角．
（2）范围：设θ是向量与的夹角，则0°≤θ≤180°.
（3）共线与垂直：若θ＝0°，则与同向；若θ＝180°，则与反向；若θ＝90°，则与垂直．
2、平面向量的数量积
（1）定义：已知两个非零向量与，它们的夹角为θ，则数量叫做与的数量积(或内积)，
记作，即，规定零向量与任一向量的数量积为0，即.
（2）几何意义：数量积等于的长度与在的方向上的投影的乘积．
【注意】（1）数量积也等于的长度|b|与在方向上的投影的乘积，这两个投影是不同的．
（2）在方向上的投影也可以写成，投影是一个数量，可正可负可为0，取决于θ角的范围．
3、向量数量积的性质
设，是两个非零向量，是单位向量，α是与的夹角，于是我们就有下列数量积的性质：
（1）.
（2）.
（3），同向⇔；，反向⇔.
特别地或.
（4）若θ为，的夹角，则.
4、平面向量数量积的运算律
（1） (交换律)．
（2） (结合律)．
（3） (分配律)．
【注意】对于实数a，b，c有，但对于向量，，而言，不一定成立，即不满足向量结合律．这是因为表示一个与c共线的向量，而表示一个与a共线的向量，而与不一定共线，所以不一定成立．
知识点5 平面向量的坐标运算
1、向量的线性运算坐标表示
（1）已知，则，．
结论：两个向量和与差的坐标分别等于这两个向量相应坐标的和与差．
（2）若，则；
结论：实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标。
2、向量平行坐标表示：已知，则向量，共线的充要条件是
3、向量数量积的坐标表示
已知非零向量，，与的夹角为θ.
一、解决向量概念问题的关键点
1、相等向量具有传递性，非零向量的平行也具有传递性．
2、共线向量即平行向量，它们均与起点无关．
3、相等向量不仅模相等，而且方向也相同，所以相等向量一定是平行向量，但平行向量未必是相等向量．
4、向量可以平移，平移后的向量与原向量是相等向量．解题时，不要把它与函数图象的平移混为一谈．
5、非零向量与的关系：是方向上的单位向量，因此单位向量与方向相同．
6、向量与数量不同，数量可以比较大小，向量则不能．但向量的模是非负实数，可以比较大小．
7、在解决向量的概念问题时，要注意两点：①不仅要考虑向量的大小，还要考虑向量的方向；②考虑零向量是否也满足条件．
【典例1】（2023·全国·高三专题练习）设为单位向量，有下列命题：①若为平面内的某个向量，则；②若与平行，则；③若与平行且，则．其中假命题的个数是（ ）
A．0 B．1 C．2 D．3
【答案】D
【解析】向量是既有大小又有方向的量，与的模相等，但方向不一定相同，故①是假命题；
若与平行，则与的方向有两种情况：
一是同向，二是反向，反向时，故②③也是假命题．
综上所述，假命题的个数是3．故选：D．
【典例2】（2023秋·福建厦门·高三校考开学考试）下列命题不正确的是（ ）
A．零向量是唯一没有方向的向量
B．零向量的长度等于0
C．若，都为非零向量，则使成立的条件是与反向共线
D．若，，则
【答案】A
【解析】A选项，零向量是有方向的，其方向是任意的，故A错误；
B选项，由零向量的定义知，零向量的长度为0，故B正确；
C选项，因为与都是单位向量，所以只有当与是相反向量，
即与是反向共线时才成立，故C正确；
D选项，由向量相等的定义知D正确.故选：A
【典例3】（2023·全国·高三专题练习）（多选）给出下列命题，不正确的有（ ）
A．若两个向量相等，则它们的起点相同，终点相同
B．若A，B，C，D是不共线的四点，且＝，则四边形ABCD为平行四边形
C．的充要条件是且
D．已知λ，μ为实数，若，则与共线
【答案】ACD
【解析】A错误，两个向量起点相同，终点相同，则两个向量相等，
但两个向量相等，不一定有相同的起点和终点；
B正确，因为＝，所以＝且，
又A，B，C，D是不共线的四点，所以四边形ABCD为平行四边形；
C错误，当且方向相反时，即使，也不能得到，
所以且不是的充要条件，而是必要不充分条件；
D错误，当时，与可以为任意向量，满足，
但与不一定共线．故选:ACD.
二、平面向量共线定理的应用
1、证明向量共线：若存在实数λ，使，则与非零向量共线；
2、证明三点共线：若存在实数λ，使，与有公共点A，则A，B，C三点共线；
3、求参数的值：利用向量共线定理及向量相等的条件列方程(组)求参数的值
【典例1】（2023·全国·高三专题练习）已知向量，不共线，且，，，则一定共线的是（ ）
A．A，B，D B．A，B，C C．B，C，D D．A，C，D
【答案】A
【解析】向量，不共线，且，，，
，则有，
而有公共点B，有A，B，D共线，A是；
，不存在实数，使得，因此不共线，A，B，C不共线，B不是；
，不存在实数，使得，因此不共线，B，C，D不共线，C不是；
，不存在实数，使得，
因此不共线，A，C，D不共线，D不是.故选：A
【典例2】（2023·全国·高三专题练习）已知向量a与b不共线，，，则与共线的条件是（ ）
A． B． C． D．
【答案】D
【解析】由，共线，得，
即，所以.故选：D.
【典例3】（2023·全国·高三专题练习）设与是两个不共线向量，且向量与共线，则 .
【答案】
【解析】依题意知向量与共线，设，
则有，所以，解得，
故答案为：
三、平面向量基本定理的实质及解题思路
1、应用平面向量基本定理表示向量的实质是平行四边形法则或三角形法则进行向量的加、减或数乘运算．
2、用平面向量基本定理解决问题的一般思路是先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．
【典例1】（2023春·重庆沙坪坝·高三重庆南开中学校考阶段练习）在中，为的中点，为边上靠近点的三等分点，记，用表示为（ ）
A． B． C． D．
【答案】D
【解析】由题知①，
②，
①＋3×②得，
故．故选：D.
【典例2】（2023秋·河南焦作·高三博爱县第一中学校考阶段练习）如图，平行四边形的对角线AC和BD交于点M，E在BC上，且，直线DE与AB的延长线交于点F，记，．

（1）试用，表示、；
（2）试用，表示．
【答案】（1），；（2）.
【解析】（1）平行四边形的对角线AC和BD交于点M，
，
.
（2）点E在BC上，且，，则，
于是，即，，
所以.
【典例3】（2023·湖南娄底·高三联考三模）2000多年前，古希腊雅典学派的第三大算学家欧道克萨斯首先提出黄金分割.所谓黄金分割点，指的是把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比，黄金分割比为.如图，在矩形中，与相交于点，，且点为线段的黄金分割点，则（ ）
A． B．
C． D．
【答案】D
【解析】由题意得，显然，，
同理有，，
所以，故，
因为，
所以.故选：D
四、平面向量数量积的3种运算方法
1、定义法求平面向量的数量积
（1）方法依据：当已知向量的模和夹角θ时，可利用定义法求解，即
（2）适用范围：已知或可求两个向量的模和夹角。
2、基底法求平面向量的数量积
（1）方法依据：选取合适的一组基底，利用平面向量基本定理将待求数量积的两个向量分别用这组基底表示出来，进而根据数量级的运算律和定义求解。
（2）适用范围：直接利用定义法求数量积不可行时，可将已知模和夹角的两个不共线的向量作为基底，采用“基底法”求解。
3、坐标法求平面向量的数量积
（1）方法依据：当已知向量的坐标时，可利用坐标法求解，
即若，，则；
（2）适用范围： = 1 \* GB3 ①已知或可求两个向量的坐标； = 2 \* GB3 ②已知条件中有（或隐含）正交基底，优先考虑建立平面直角坐标系，使用坐标法求数量积。
【典例1】（2023·四川宜宾·校考三模）若四边形是边长为2的菱形，，分别为的中点，则（ ）
A． B． C． D．
【答案】A
【解析】因为四边形是边长为2的菱形，，
所以.
所以
，故选：A
【典例2】（2023·陕西西安·校联考模拟预测）在边长为2的正三角形ABC中，，，则（ ）
A． B． C． D．
【答案】B
【解析】由题知，为中点，为中点，连接，以为坐标原点，
分别以，所在的直线为轴，轴建立如图所示的平面直角坐标系，
则，，，，，
所以，，故．故选：B
【典例3】（2023·全国·高三专题练习）正方形的边长是2，是的中点，则（ ）
A． B．3 C． D．5
【答案】B
【解析】方法一：以为基底向量，可知，
则，
所以；
方法二：如图，以为坐标原点建立平面直角坐标系，
则，可得，
所以；
方法三：由题意可得：，
在中，由余弦定理可得，
所以.故选：B.
五、求向量模或其范围的常用方法
1、定义法：利用及，把向量的模的运算转化为数量积运算；
2、坐标法：当向量有坐标或适合建坐标系时，可用模的计算公式；
3、几何法，利用向量的几何意义，即利用向量加减法的平行四边形法则或三角形法则作出向量，再利用余弦定理等方法求解．
【典例1】（2023·全国·河南省实验中学校考模拟预测）已知向量，线段的中点为，且，则（ ）
A． B． C． D．
【答案】A
【解析】设，
则，
由，
得，又已知，且，
则有，
故.故选：A.
【典例2】（2023·四川遂宁·高三校考模拟预测）已知平面向量，，的夹角为，，则实数（ ）
A． B．1 C． D．
【答案】A
【解析】因为，所以，
即，解得.故选：A.
【典例3】（2023·全国·高三专题练习）已知为单位向量，且，向量满足，则的取值范围为（ ）
A． B． C． D．
【答案】B
【解析】因为，所以，
设，，
由，得，即，
即，又，
所以，解得，
所以的取值范围为.故选：B.
六、从动态角度理解三角形四心的向量表示
1、常见重心向量式：设O是∆ABC的重心，P为平面内任意一点
= 1 \* GB3 ①OA+OB+OC=0
= 2 \* GB3 ②PO=13PA+PB+PC
= 3 \* GB3 ③若AP=λAB+AC或OP=OA+λAB+AC，λ∈[0,+∞)，则P一定经过三角形的重心
= 4 \* GB3 ④若AP=λABABsinB+ACACsinC或OP=OA+λABABsinB+ACACsinC，λ∈[0,+∞)则P一定经过三角形的重心
2、常见垂心向量式：O是∆ABC的垂心，则有以下结论：
= 1 \* GB3 ①OA∙OB=OB∙OC=OC∙OA
= 2 \* GB3 ②OA2+BC2=OB2+CA2=OC2+AB2
= 3 \* GB3 ③动点P满足OP=OA+λABABcsB+ACACcsC，λ∈0,+∞，则动点P的轨迹一定通过∆ABC的垂心
3、常用外心向量式：O是∆ABC的外心，
= 1 \* GB3 ①OA=OB=OC⟺OA2=OB2=OC2
= 2 \* GB3 ②OA+OB∙AB=OB+OC∙BC=OA+OC∙AC=0
= 3 \* GB3 ③动点P满足OP=OB+OC2+λABABcsB+ACACcsC，λ∈0,+∞，则动点P的轨迹一定通过∆ABC的外心.
= 4 \* GB3 ④若OA+OB∙AB=OB+OC∙BC=OC+OA∙CA=0，则O是∆ABC的外心.
4、常见内心向量式：P是∆ABC的内心，
= 1 \* GB3 ①ABPC+BCPA+CAPB=0（或aPA+bPB+cPC=0）
其中a，b，c分别是∆ABC的三边BC、AC、AB的长，
= 2 \* GB3 ②AP=λABAB+ACAC，λ[0,+∞)，则P一定经过三角形的内心。
【典例1】（2023·全国·高三专题练习）在中，若，则点是的（ ）
A．重心 B．内心 C．垂心 D．外心
【答案】B
【解析】过点分别作，，的垂线，，，其垂足依次为，如图所示，
由于，
根据奔驰定理就有：，
即，
因此，故点是的内心，B选项正确.故选：B
【典例2】（2023·全国·高三专题练习）设为的外心，若，则点是的（ ）
A．重心 B．内心 C．垂心 D．外心
【答案】C
【解析】取BC的中点D，如图所示，
连接OD，AM，BM，CM．
因为，所以，
又，则，所以，
又由于为的外心，所以，
因此有．同理可得，，
所以点是的垂心．故选：C．
【典例3】（2023·全国·高三专题练习）在中，给出如下命题:
①是所在平面内一定点，动点满足，，则动点的轨迹一定过的重心．
②是所在平面内一定点，动点满足，，则动点的轨迹一定过的内心．
③是所在平面内一定点，且，则．
（4）若，且，则是等边三角形．
其中正确的命题有 个．
【答案】3
【解析】对于①，令点为BC的中点，由于，，
根据极化恒等式就有，，
于是，，
因此动点的轨迹是射线AD，过的重心，故①正确．
对于②，取一点使得，并连接AD，如图所示，
由于，因此，于是，
从而的内心在射线AD上．
由于，，
于是就有，，
即，，
因此动点的轨迹是射线AD，过的内心，故②正确．
对于③，由，可得设的中点为，,
所以，故③错误．
对于④，根据，结合②，可得的平分线与BC垂直，
于是就有．由于，
又，得到，因此是等边三角形，故④正确．
综上所述，正确的命题有3个．
故答案为：
七、平面向量最值范围问题的常用方法
1、定义法
第1步：利用向量的概念及其基本运算将所求的问题转化为相应的等式关系；
第2步：运用基本不等式求其最值问题；
第3步：得出结论。
2、坐标法
第1步：根据题意建立适当的直角坐标系，并推导关键点的坐标；
第2步：将平面向量的运算坐标化；
第3步：运用适当的数学方法如二次函数、基本不等式的思想、三角函数思想等求解。
3、基底法
第1步：利用基底转化向量；
第2步：根据向量运算化简目标；
第3步：运用适当的数学方法如二次函数、基本不等式的思想、三角函数等得出结论；
4、几何意义法
第1步：结合条件进行向量关系推导；
第2步：利用向量之间的关系确定向量所表达的点的轨迹；
第3步：结合图形，确定临界位置的动态分析求出范围。
【典例1】（2023·全国·高三专题练习）在中，，D为BC的中点，点P在斜边BC的中线AD上，则的取值范围为（ ）
A． B． C． D．
【答案】A
【解析】以为坐标原点，为轴的正方向建立平面直角坐标系，
所以，
因为D为BC的中点，所以，，
设，所以，所以，
可得，，
所以，
因为，所以.故选：A.
【典例2】（2023秋·辽宁沈阳·高三沈阳市第一二〇中学校考阶段练习）已知正方形的边长为2，对角线相交于点是线段上一点，则的最小值为 ．
【答案】
【解析】记，设，
因为，
所以，
因为，
所以，
所以，当时，取得最小值.
故答案为：
【典例3】（2023·全国·高三专题练习）在直角中，，平面内动点满足，则的最小值为 .
【答案】/
【解析】平面内动点满足，所以点的轨迹是以为圆心，1为半径的圆，
因为，由勾股定理可得：，
所以，且，
所以，所以，
，
，
，
，
又向量是长度为的一个向量，由此可得，点在圆上运动，
当与共线反向时，取最小值，且这个最小值为一，
故的最小值为.
故答案为：.
易错点1 平面向量的概念模糊，尤其是零向量
点拨：平面向量部分概念多而抽象，如零向量、单位向量、平行向量、共线向量、相等向量、相反向量、向量的加法、减法、数乘、数量积、向量的模、夹角等等。
【典例1】（2023·全国·高三专题练习）下列命题中，正确的是（ ）
A．若，，则
B．若则或
C．对于任意向量，有
D．对于任意向量，有
【答案】D
【解析】对于A，当时，满足，，但不一定平行，故A错误；
对于B，当，时，满足，但，不成立，故B错误；
对于C，若非零向量方向相反，则，故C错误；
对于D，当中有零向量时，；
当为非零向量时，若共线且方向相同时，则，
当为非零向量时，若共线且方向相反时，则，
当为非零向量时，且不共线时，如图所示，，
综上，，故D正确．故选：D．
【典例2】（2023·全国·高三专题练习）已知两个非零向量与共线，下列说法不正确的是（ ）
A．或 B．与平行 C．与方向相同或相反 D．存在实数，使得
【答案】A
【解析】非零向量与共线，
对于A，，，故A错误；
对于B，∵向量与共线，∴向量与平行，故B正确；
对于C，∵向量与共线，∴与方向相同或相反，故C正确；
对于D，∵与共线，∴存在实数，使得，故D正确．故选:A．
【典例3】（2023·全国·高三专题练习）（多选）下列命题正确的是（ ）
A．若都是单位向量，则.
B．“”是“”的必要不充分条件
C．若都为非零向量，则使＋＝成立的条件是与反向共线
D．若，则
【答案】BCD
【解析】对A，都是单位向量，则模长相等，但方向不一定相同，
所以得不到，A错误；
对B，“”推不出“”，但 “”能推出 “”，
所以“”是“”的必要不充分条件，B正确；
对C，因为与反向共线，
且，都为单位向量，则＋＝，C正确；
对D，若，则，D正确，故选:BCD.
易错点2 忽视两个向量成为基底的条件
点拨：如果、是同一平面内的两个不共线向量，那么对该平面内的任一向量，有且只有一对实数，，使。在平面向量知识体系中，基本定理是基石，共线向量定理是重要工具。考生在学习这部分知识时，务必要注意这两个定理的作用和成立条件。
【典例1】（2023·四川宜宾·宜宾市叙州区第一中学校校考二模）设，下列向量中，可与向量组成基底的向量是（ ）
A． B． C． D．
【答案】C
【解析】对于AB项，若时，，不满足构成基向量的条件，所以AB都错误；
对于D项，若时，不满足构成基向量的条件，所以D错误；
对于C项，因为，又因为恒成立，
说明与不共线，复合构成基向量的条件，所以C正确.故选：C
【典例2】（2022·全国·高三专题练习）设是平面内两个不共线的向量，则向量可作为基底的是（ ）
A． B．
C． D．
【答案】C
【解析】对于A，因为，
所以共线，所以不能作为基底，所以A不合题意；
对于B，因为，
所以共线，所以不能作为基底，所以B不合题意；
对于C，若共线，则存在唯一实数，使，即，
所以且，所以不存在，所以不共线，
所以可以作为基底，所以C符合题意；
对于D，因为，
所以共线，所以不能作为基底，所以D不合题意，故选：C
【典例3】（2022·全国·高三专题练习）在下列向量组中，不能把向量表示出来的是（ ）
A．， B．，
C．， D．，
【答案】ABD
【解析】对于A：是零向量与共线，而与不共线，
所以和不能表示，故选项A符合题意；
对于B：，故和共线，则和只能表示与它们共线的向量，
而与和不共线，所以和不能表示，故选项B符合题意；
对于C：因为，所以，不共线，
则和能表示，故选项C不符合题意；
对于D：，所以和共线，则和只能表示与它们共线的向量，
而与和不共线，所以和不能表示，故选项D符合题意；故选：ABD.
易错点3 错误使用向量平行的等价条件
点拨：对于，，，若是使用，容易忽略0这个解.考生解题过程中要注意等价条件的完备性。
【典例1】（2022秋·浙江绍兴·高三统考期末）已知平面向量，若，则实数的值为（ ）
A． B． C． D．
【答案】C
【解析】由题，有.
又，则，
又，则.故选：C
【典例2】（2023春·甘肃张掖·高三校考阶段练习）设向量，，若，的方向相反，则 ．
【答案】3
【解析】因为，的方向相反，所以，共线，
所以，即，解得或．
当时，，符合题意；
当时，，不符合题意，舍去．故答案为：3.
易错点4 混淆向量数量积运算和数乘运算的结果
点拨：向量的数乘运算结果依旧为向量，而数量积的运算结果为实数，两者要区分开。尤其使用数量积的运算时不可约公因式。
【典例1】（2022·全国·高三专题练习）（多选）已知、、均为非零向量，下列命题错误的是（ ）
A．， B．可能成立
C．若，则 D．若，则或
【答案】ACD
【解析】仍是向量，不是向量，A错；
不妨取，，，则，
，此时，B对；
若，，，则，但，C错；
若，，则，但，，D错.故选：ACD.
【典例2】（2023秋·黑龙江牡丹江·高三校考阶段练习）（多选）下列关于平面向量，，的运算，一定成立的有（ ）
A． B．
C． D．
【答案】ACD
【解析】对于A：根据平面向量数量积的分配律可知一定成立，故A正确；
对于B：由数量积的结果为数量，则表示与共线的向量，
表示与共线的向量，则与不一定相同，即B错误；
对于C：设与的夹角为，则，因为，
所以，故C正确；
对于D：，，
由C知，所以，
即，即，故D正确；故选：ACD
易错点5 确定向量夹角时忽略向量的方向
点拨：错误理解向量的夹角，在使用求解时，特别注意，要共起点才能找夹角，否则使用的可能是其补角造成错误。
【典例1】（2022秋·山东·高三校联考阶段练习）在中，，，，则为（ ）
A． B． C． D．
【答案】A
【解析】由，，
，
，则，
作图如下：在中，，
易知向量与的夹角，
.故选：A.
【典例2】（2023·山西大同·高三统考模拟预测）已知在边长为3的等边中，，则 ．
【答案】6
【解析】如图，
．
故答案为：6
【典例3】（2024秋·湖北武汉·高三统考开学考试）正六边形的边长为4，点满足，则 .
【答案】24
【解析】因为，故，即，
故
.
故答案为：
易错点6 忽视两向量夹角的取值范围
点拨：向量的夹角范围是从，解题时易忽略夹角为0和夹角为的情况。
【典例1】（2023·河南·河南省内乡县高级中学校考模拟预测）已知，与的夹角为45°，求使向量与的夹角是锐角，则的取值范围 .
【答案】
【解析】
，
由向量与的夹角是锐角，，解得或；
且向量与不共线，则，解得，
所以的取值范围为.
故答案为：.
【典例2】（2022秋·辽宁葫芦岛·高三校联考阶段练习）已知向量，，若与的夹角为钝角，则整数的一个取值可以是 .
【答案】（或，，，，，，，填写一个答案即可）
【解析】因为与的夹角为钝角，所以，
所以，
若与平行，即，所以，
化简得，得，其中当时，与反向平行，
故整数的取值可以是，，，，，，，.
故答案为：（或，，，，，，，填写一个答案即可）
【典例3】（2023·全国·高三专题练习）已知，，且关于的方程有实根，则与的夹角的取值范围是（ ）
A． B． C． D．
【答案】B
【解析】因为关于的方程有实根，
所以，
所以，，所以，
即与的夹角的取值范围是.故选：B.向量运算
定义
法则(或几何意义)
运算律
加法
求两个向量和的运算

交换律：；
结合律：
减法
求与的相反向量的和的运算
数乘
求实数λ与向量的积的运算
，
当λ>0时，与的方向相同；
当λ