初中数学华师大版八年级下册1. 一次函数教学演示ppt课件

这是一份初中数学华师大版八年级下册1. 一次函数教学演示ppt课件，共24页。PPT课件主要包含了新课导入，进行新课，问题1，从图上怎么看出来，归纳小结，y2x-5，y-x+1，yx+5，随堂练习，利用图象解方程组等内容，欢迎下载使用。
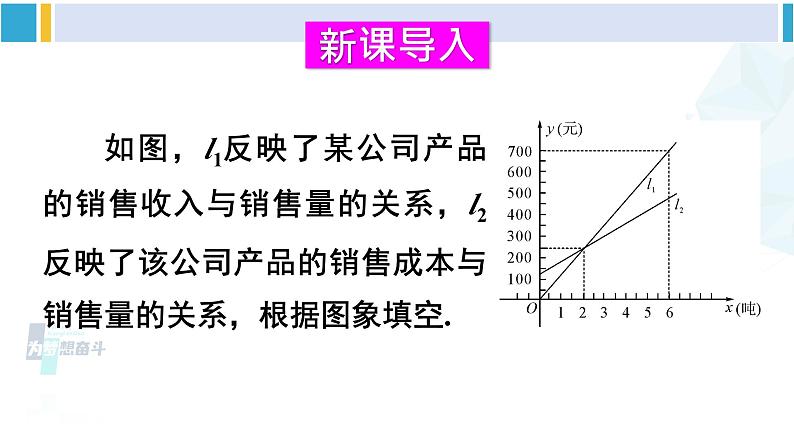
如图，l1反映了某公司产品的销售收入与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，根据图象填空.
①当销售量为2吨时，销售收入=____元，销售成本=____元； ②当销售量为6吨时，销售收入=____元，销售成本=____元；
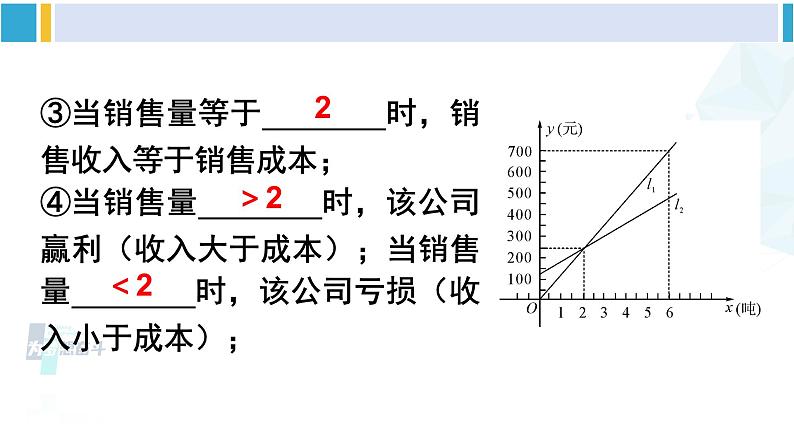
③当销售量等于________时，销售收入等于销售成本； ④当销售量________时，该公司赢利（收入大于成本）；当销售量________时，该公司亏损（收入小于成本）；
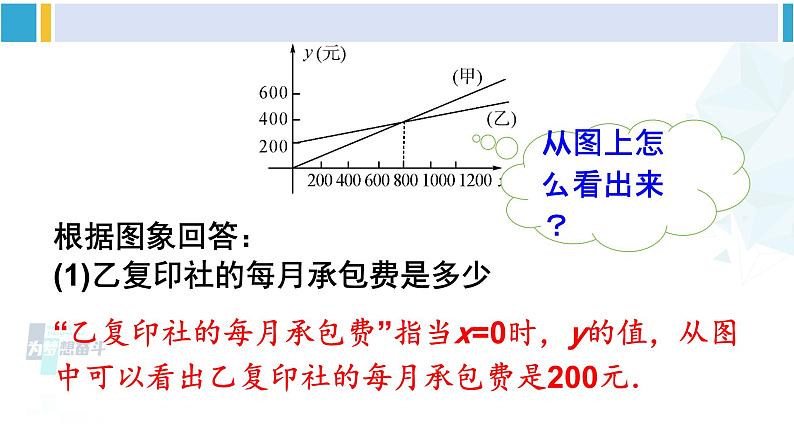
学校每个月都有一些复印任务，原来由甲复印社承接，按每100页40元计费.现在乙复印社表示：若学校先按月付给一定数额的承包费，则可按每100页15元收费.两复印社每月收费情况如图所示.
根据图象回答：(1)乙复印社的每月承包费是多少
“乙复印社的每月承包费”指当x=0时，y的值，从图中可以看出乙复印社的每月承包费是200元．
(2)当每月复印多少时，两复印社实际收费相同？
思考：“收费相同”，在图象上怎样反映出来？
“收费相同”是指当x取相同的值时，y相等，即两条射线的交点．我们看到，两个一次函数图象的交点处，自变量和对应的函数值同时满足两个函数的关系式．而两个一次函数的关系式就是方程组中的两个方程，所以交点的坐标就是方程组的解．据此，我们可以利用图象来求某些方程组的解．
(3)如果每月复印页数在1200页左右，应选择哪个复印社？
思考：如何在图象上看出函数值的大小？
作一条x轴的垂线，如图，此时x的值相同，它与哪一条射线的交点较高，就表示对应函数值较大，收费就较高；反之，它与另一条射线的交点较低，就表示对应函数值较小，收费就较低．从图中可以看出，如果每月复印页数在1200页左右，那么应选择乙复印社收费较低．
两个一次函数图象的交点处，自变量和对应的函数值同时满足两个函数的关系式．而两个一次函数的关系式就是方程组中的两个方程，所以交点的坐标就是方程组的解．据此，我们可以利用图象来求某些方程组的解．
例如，图中的两条直线：y=2x-5和y=-x+1，它们的交点坐标(2,-1)就是方程组 的解
例 利用一次函数的图像，求二元一次方程组 的解.
如图，分别作出一次函数y=x+5和 的图像，得到它们交点的坐标(-4,1)，即方程组的解为
1.小张准备将平时的零用钱节约一些储存起来．他已存有50元，从现在起每个月存12元．小张的同学小王以前没有存过零用钱，听到小张在存零用钱，表示从小张存款当月起每个月存18元，争取超过小张．请你写出小张和小王存款和月份之间的函数关系，并计算半年以后小王的存款是多少，能否超过小张？至少几个月后小王的存款能超过小张？
解:设小张存x个月的存款是y1元，小王的存x个月的存款是y2元，则y1=50＋12x，y2=18x，
解:在直角坐标系中画出两条直线，如下图所示．
两条直线的交点坐标是(2,-1)，所以方程组的解为
3.下图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象（分别是正比例函数图象和一次函数图象）．根据图象解答下列问题：
(1)请分别求出表示轮船和快艇行驶过程的函数解析式（不要求写出自变量的取值范围）； (2)轮船和快艇在途中（不包括起点和终点）行驶的速度分别是多少？ (3)问快艇出发多长时间赶上轮船？
解:(1)设表示轮船行驶过程的函数解析式y=kx(k≠0),由图象知：当x=8时，y=160．代入上式，得8k=160,可解得k=20．所以轮船行驶过程的函数解析式为y=20x．设表示快艇行驶过程的函数解析式为y=ax＋b(a≠0),由图象知：当x=2时，y=0；当x=6时，y=160．代入上式，得 可解得
所以快艇行驶过程的函数解析式为y=40x－80．
(2)由图象可知，轮船在8小时内行驶了160km，快艇在4小时内行驶了160km，所以轮船的速度是160/8=20(km/h)，快艇的速度是160/4=40(km/h)．
(3)设轮船出发x小时快艇赶上轮船，20x=40x-80,得x=4,4－2=2．答:快艇出发了2小时赶上轮船.
谈谈你在这节课中，有什么收获？