



还剩19页未读,
继续阅读
所属成套资源:华师大版八年级数学下册【精品教学课件】
成套系列资料,整套一键下载
华师大版八年级数学下册 第19章 矩形、菱形与正方形 1.菱形的性质(课件)
展开
这是一份华师大版八年级数学下册 第19章 矩形、菱形与正方形 1.菱形的性质(课件),共27页。
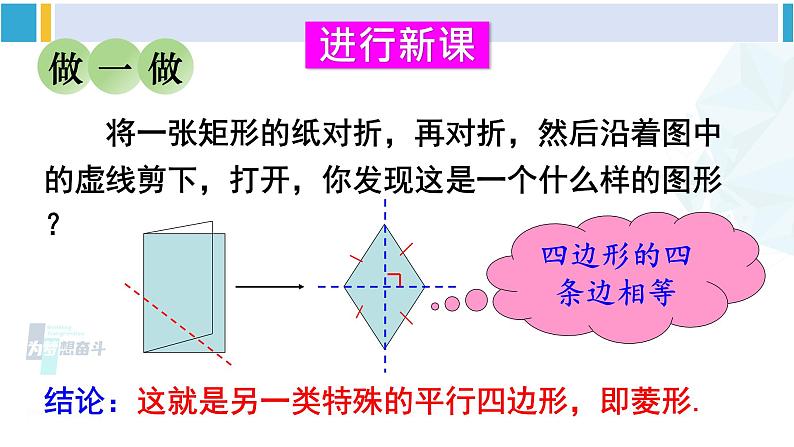
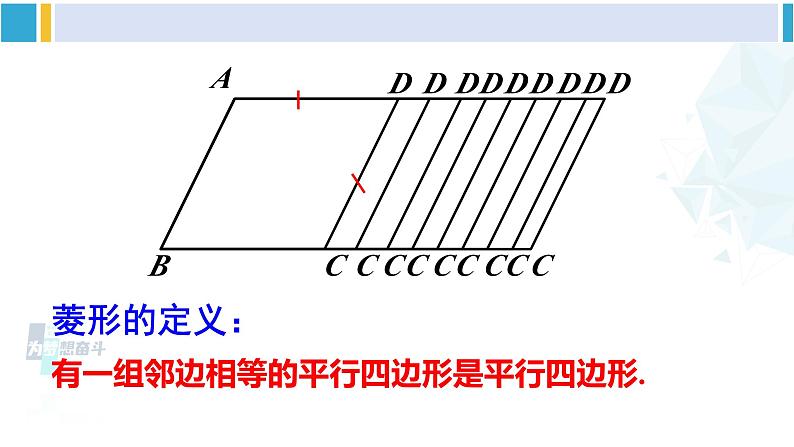
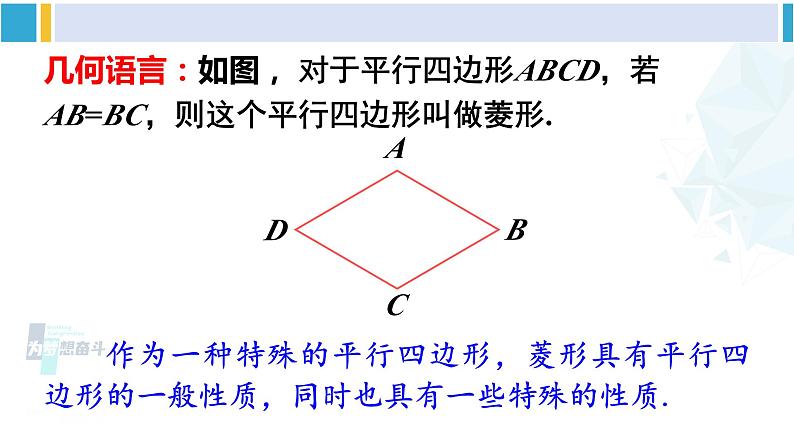
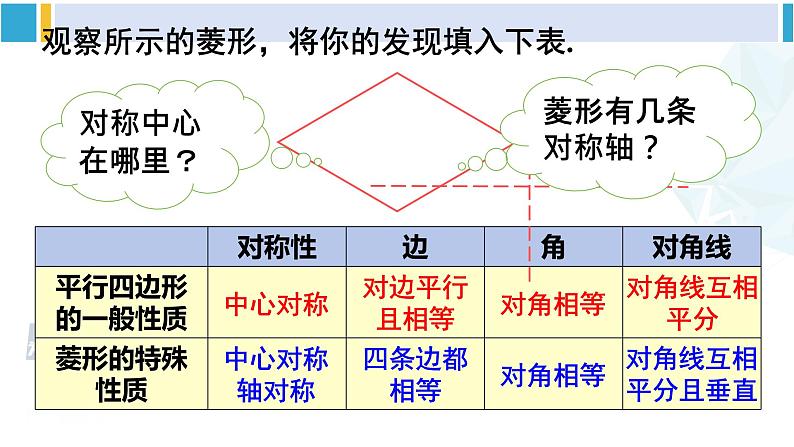
19.2 菱 形1 菱形的性质华东师大·八年级数学下册新课导入回顾复习 平行四边形有哪些特征?矩形与平行四边形比较有哪些特殊的特征?平行四边形对边平行且相等对角相等邻角互补对角线互相平分矩形四个角是直角对角线相等观察图案,有没有你熟悉的图形?进行新课 将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形?四边形的四条边相等结论:这就是另一类特殊的平行四边形,即菱形.AB菱形的定义:有一组邻边相等的平行四边形是平行四边形.几何语言:如图, 对于平行四边形ABCD,若AB=BC,则这个平行四边形叫做菱形. 作为一种特殊的平行四边形,菱形具有平行四边形的一般性质,同时也具有一些特殊的性质.中心对称对边平行且相等对角相等对角线互相平分中心对称轴对称四条边都相等对角相等对角线互相平分且垂直观察所示的菱形,将你的发现填入下表.菱形有几条对称轴?对称中心在哪里? 如图,我们发现,菱形既是中心对称图形,也是轴对称图形,对称轴为它的对角线所在的直线. 由此,很容易猜想菱形所具有的特殊性质:菱形的性质定理1: 菱形的四条边都相等.菱形的性质定理2: 菱形的对角线互相垂直.证明:(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC.∴AB=BC=DC=DA.已知:四边形ABCD是菱形,求证:(1)AB=BC=CD=DA. (2)AC⊥BD,AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.(2)在△DAC中,∵AO=CO∴DB⊥AC,DB平分∠ADC(三线合一).同理:DB平分∠ABC;AC平分∠DAB和∠DCB.例1 如图,在菱形ABCD中,∠BAD=2∠B.试求出∠B的大小,并说明△ABC是等边三角形.解 在菱形ABCD中,∵∠B+∠BAD=180°,∠BAD=2∠B,∴ ∠B=60°在菱形ABCD中,∵AB=BC(菱形的四条边都相等),∠B=60°,∴△ABC是等边三角形.感受生活例2 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.(结果保留根号)ABCDO解 ∵四边形ABCD是菱形,∴OB=OD,AB=AD(菱形的四条边都相等)在△ABO和△ADO中,∵AB=AD,AO=AO,OB=OD,∴△ABO≌△ADO,例3 如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.E解 ∵四边形ABCD是菱形,∴AD=DC=CB=BA(菱形的四条边都相等).又∵AE垂直平分CD,∴AC=AD,∴AC=AD=DC=CB=BA,即△ADC与△ABC都为等边三角形,∴∠ACD=∠ACB=60°.∴∠BCD=120°.随堂练习1. 一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的四个内角的度数为 _________________ .60°120°60°120°2.菱形具有而平行四边形不一定具有的特征是( )A.对角线互相平分 B.对边相等且平行C.对角线平分一组对角 D.对角相等C3. 已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,菱形的边长是____cm.4. 菱形ABCD的周长为40cm,两条对角AC∶BD=4:3,那么对角线AC=____cm,BD=____cm. 5 16125. 已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 求证:∠AEF=∠AFE.证明:如图,连接AC,∵四边形ABCD为菱形,∴BC=CD,∠ECA=∠FCA.又∵BE=DF,∴EC=FC.∴△AEC≌△AFC,∴AE=AF,∴∠AEF=∠AFE.6. 如图,已知菱形ABCD的周长为24cm,对角线AC的长为8cm,求菱形的面积.解:∵菱形的周长为24cm,∴AB=6cm,又AC=8cm,∴OA=4cm,因为AC⊥BD,∴OB= 2 (cm),∴BD=4 ,∴菱形ABCD的面积= AC·BD = ×8×4 =16 (cm2)课堂小结谈谈你在这节课中,有什么收获?课后作业1.从课后习题中选取;2.完成练习册本课时的习题.
19.2 菱 形1 菱形的性质华东师大·八年级数学下册新课导入回顾复习 平行四边形有哪些特征?矩形与平行四边形比较有哪些特殊的特征?平行四边形对边平行且相等对角相等邻角互补对角线互相平分矩形四个角是直角对角线相等观察图案,有没有你熟悉的图形?进行新课 将一张矩形的纸对折,再对折,然后沿着图中的虚线剪下,打开,你发现这是一个什么样的图形?四边形的四条边相等结论:这就是另一类特殊的平行四边形,即菱形.AB菱形的定义:有一组邻边相等的平行四边形是平行四边形.几何语言:如图, 对于平行四边形ABCD,若AB=BC,则这个平行四边形叫做菱形. 作为一种特殊的平行四边形,菱形具有平行四边形的一般性质,同时也具有一些特殊的性质.中心对称对边平行且相等对角相等对角线互相平分中心对称轴对称四条边都相等对角相等对角线互相平分且垂直观察所示的菱形,将你的发现填入下表.菱形有几条对称轴?对称中心在哪里? 如图,我们发现,菱形既是中心对称图形,也是轴对称图形,对称轴为它的对角线所在的直线. 由此,很容易猜想菱形所具有的特殊性质:菱形的性质定理1: 菱形的四条边都相等.菱形的性质定理2: 菱形的对角线互相垂直.证明:(1)∵四边形ABCD是菱形∴DA=DC(菱形的定义)∵DA=BC,AB=DC.∴AB=BC=DC=DA.已知:四边形ABCD是菱形,求证:(1)AB=BC=CD=DA. (2)AC⊥BD,AC平分∠DAB和∠DCB,BD平分∠ADC和∠ABC.(2)在△DAC中,∵AO=CO∴DB⊥AC,DB平分∠ADC(三线合一).同理:DB平分∠ABC;AC平分∠DAB和∠DCB.例1 如图,在菱形ABCD中,∠BAD=2∠B.试求出∠B的大小,并说明△ABC是等边三角形.解 在菱形ABCD中,∵∠B+∠BAD=180°,∠BAD=2∠B,∴ ∠B=60°在菱形ABCD中,∵AB=BC(菱形的四条边都相等),∠B=60°,∴△ABC是等边三角形.感受生活例2 如图,已知菱形ABCD的边长为2cm,∠BAD=120°,对角线AC、BD相交于点O.试求这个菱形的两条对角线AC与BD的长.(结果保留根号)ABCDO解 ∵四边形ABCD是菱形,∴OB=OD,AB=AD(菱形的四条边都相等)在△ABO和△ADO中,∵AB=AD,AO=AO,OB=OD,∴△ABO≌△ADO,例3 如图,菱形ABCD的对角线AC与BD相交于点O,AE垂直且平分CD,垂足为点E.求∠BCD的大小.E解 ∵四边形ABCD是菱形,∴AD=DC=CB=BA(菱形的四条边都相等).又∵AE垂直平分CD,∴AC=AD,∴AC=AD=DC=CB=BA,即△ADC与△ABC都为等边三角形,∴∠ACD=∠ACB=60°.∴∠BCD=120°.随堂练习1. 一个菱形的周长为8cm,一条对角线长为2 cm.则这个菱形的四个内角的度数为 _________________ .60°120°60°120°2.菱形具有而平行四边形不一定具有的特征是( )A.对角线互相平分 B.对边相等且平行C.对角线平分一组对角 D.对角相等C3. 已知四边形ABCD是菱形,O是两条对角线的交点,AC=8cm,DB=6cm,菱形的边长是____cm.4. 菱形ABCD的周长为40cm,两条对角AC∶BD=4:3,那么对角线AC=____cm,BD=____cm. 5 16125. 已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 求证:∠AEF=∠AFE.证明:如图,连接AC,∵四边形ABCD为菱形,∴BC=CD,∠ECA=∠FCA.又∵BE=DF,∴EC=FC.∴△AEC≌△AFC,∴AE=AF,∴∠AEF=∠AFE.6. 如图,已知菱形ABCD的周长为24cm,对角线AC的长为8cm,求菱形的面积.解:∵菱形的周长为24cm,∴AB=6cm,又AC=8cm,∴OA=4cm,因为AC⊥BD,∴OB= 2 (cm),∴BD=4 ,∴菱形ABCD的面积= AC·BD = ×8×4 =16 (cm2)课堂小结谈谈你在这节课中,有什么收获?课后作业1.从课后习题中选取;2.完成练习册本课时的习题.
相关资料
更多









