中考数学几何模型专项复习 模型09 三角形——老鹰抓小鸡模型-（原卷版+解析）

这是一份中考数学几何模型专项复习 模型09 三角形——老鹰抓小鸡模型-（原卷版+解析），共12页。

（筝型或折叠模型）

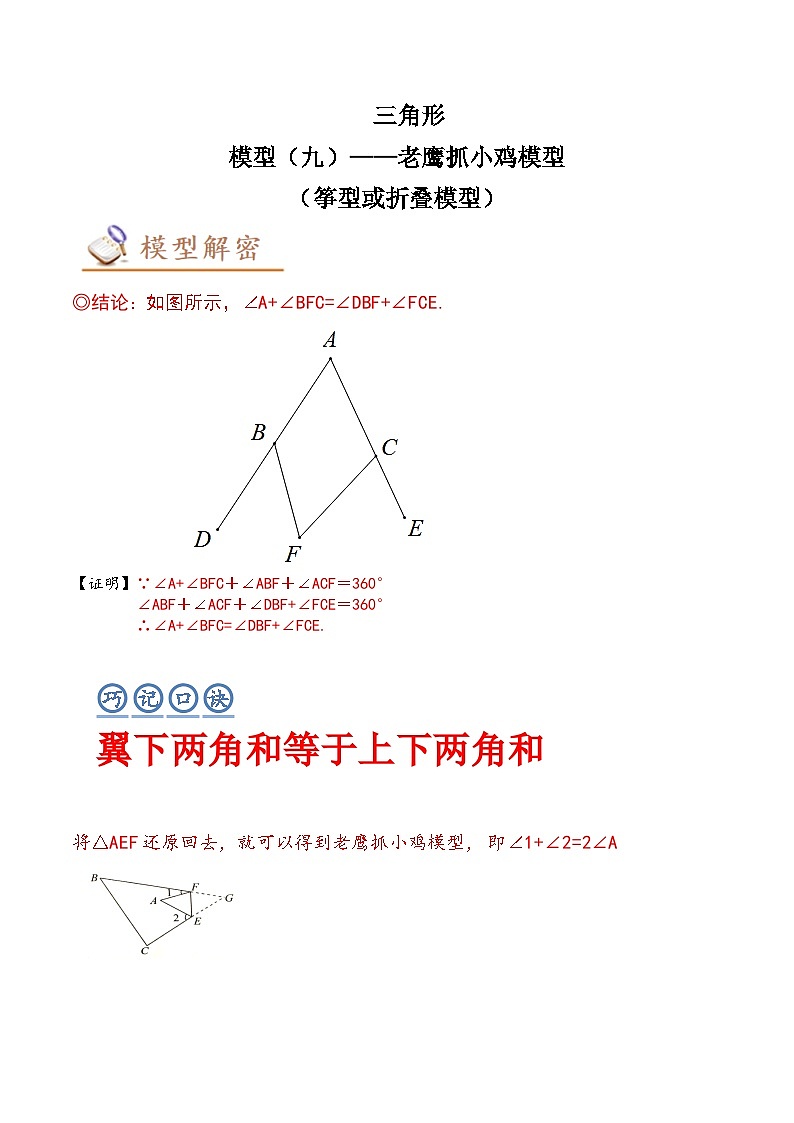
◎结论：如图所示，∠A+∠BFC=∠DBF+∠FCE.

【证明】∵∠A+∠BFC＋∠ABF＋∠ACF＝360°
∠ABF＋∠ACF＋∠DBF+∠FCE＝360°
∴∠A+∠BFC=∠DBF+∠FCE.
eq \\ac(○,巧) eq \\ac(○,记) eq \\ac(○,口) eq \\ac(○,诀)
翼下两角和等于上下两角和
将△AEF还原回去，就可以得到老鹰抓小鸡模型， 即∠1+∠2=2∠A
注：老鹰抓小鸡模型的变形比较多 ，大多考查翻折类问题的角度关系，分为①折叠后角的顶点落在角的内部，②以及角的顶点落在角的外部，记住结论能节省大量的答题时间.
1．(2023·江苏·宿迁青华中学七年级阶段练习）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝120°，则∠1+∠2的度数为（ ）
A．90°B．100°C．110°D．120°
2．(2023·全国·八年级课时练习）如图，把△ABC沿EF对折，折叠后的图形如图所示，，，则 的度数为（ ）
A．B．C．D．
3．(2023·福建泉州·七年级期末）如图，已知三角形纸片中，，，将纸片的一角折叠，使点落则在内，若，则的度数为（ ）
A．B．C．D．
1．(2023·海南海口·七年级期末）如图，把△ABC纸片沿MN折叠，使点C落在△ABC内部点C′处，若∠C=36°，则∠1+∠2等于（ ）
A．54°B．62°C．72°D．76°
2．(2023·河南·淮阳第一高级中学七年级期末）如图，已知点，分别在的边，上，将沿折叠，使点落在点的位置，已知，则的度数为（ ）
A．B．C．D．
3．(2023·全国·八年级课时练习）如图，把纸片沿折叠，使点落在图中的处，若，，则的大小为______.
1．（2012·广东河源·中考真题）如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A′重合，若∠A=75°，则∠1+∠2=【 】
A．150°B．210°C．105°D．75°
2．(2023·广东梅州·一模）如图，在△ABC中，点D、E分别为边BC、AC上的点，将△CDE沿DE翻折得到△C′DE，使C′D∥AB．若∠A＝75°，∠C=45°，则∠C′EA的大小为 _____°．
三角形
模型（九）——老鹰抓小鸡模型
（筝型或折叠模型）

◎结论：如图所示，∠A+∠BFC=∠DBF+∠FCE.

【证明】∵∠A+∠BFC＋∠ABF＋∠ACF＝360°
∠ABF＋∠ACF＋∠DBF+∠FCE＝360°
∴∠A+∠BFC=∠DBF+∠FCE.
eq \\ac(○,巧) eq \\ac(○,记) eq \\ac(○,口) eq \\ac(○,诀)
翼下两角和等于上下两角和
将△AEF还原回去，就可以得到老鹰抓小鸡模型， 即∠1+∠2=2∠A
注：老鹰抓小鸡模型的变形比较多 ，大多考查翻折类问题的角度关系，分为①折叠后角的顶点落在角的内部，②以及角的顶点落在角的外部，记住结论能节省大量的答题时间.
1．(2023·江苏·宿迁青华中学七年级阶段练习）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝120°，则∠1+∠2的度数为（ ）
A．90°B．100°C．110°D．120°
答案:D
分析连接A'A，先求出∠BAC，再证明∠1+∠2=2∠BAC即可解决问题．
【详解】解：如图，连接AA'，
∵A'B平分∠ABC，A'C平分∠ACB，
∴∠A'BC=∠ABC，∠A'CB=∠ACB，
∵∠BA'C=120°，
∴∠A'BC+∠A'CB=180°-120°=60°，
∴∠ABC+∠ACB=120°，
∴∠BAC=180°-120°=60°，
∵沿DE折叠，
∴∠DAA'=∠DA'A，∠EAA'=∠EA'A，
∵∠1=∠DAA'+∠DA'A=2∠DAA'，∠2=∠EAA'+∠EA'A=2∠EAA'，
∴∠1+∠2=2∠DAA'+2∠EAA'=2∠BAC=2×60°=120°，
故选：D．
【点睛】本题考查了三角形内角和定理、角平分线定义、三角形外角的性质、折叠变换等知识，解题的关键是正确添加辅助线，灵活应用所学知识，属于中考常考题型．
2．(2023·全国·八年级课时练习）如图，把△ABC沿EF对折，折叠后的图形如图所示，，，则 的度数为（ ）
A．B．C．D．
答案:B
分析由三角形的内角和，得，由邻补角的性质得，根据折叠的性质得，即，所以，．
【详解】解：∵，
∴，
∴，
由折叠的性质可得：
，
∴，
∵，
∴，
即．
故选B．
【点睛】本题考查了三角形的内角和定理、邻补角的性质、折叠的性质，熟悉掌握三角形的内角和为，互为邻补角的两个角之和为以及折叠的性质是本题的解题关键．
3．(2023·福建泉州·七年级期末）如图，已知三角形纸片中，，，将纸片的一角折叠，使点落则在内，若，则的度数为（ ）
A．B．C．D．
答案:B
分析延长和，交于点，根据三角形内角和定理求出的度数，根据折叠的性质得：，，求出的度数，根据三角形内角和定理求出的度数，得到的度数，从而得出的度数．
【详解】解：如图，延长和，交于点，
∵，，
∴，
根据折叠的性质得：，，
∵，
∴，
∴，
∴，
∴，
∴．
故选：B．
【点睛】本题考查翻折变换（折叠问题），三角形内角和定理．延长和，交于点，根据三角形内角和定理和折叠的性质求角的度数是解题的关键．
1．(2023·海南海口·七年级期末）如图，把△ABC纸片沿MN折叠，使点C落在△ABC内部点C′处，若∠C=36°，则∠1+∠2等于（ ）
A．54°B．62°C．72°D．76°
答案:C
分析根据折叠可知∠C=∠，四边形内角和为360°，即可求出+，用平角的定义即可求出∠1+∠2
【详解】∵△CMN折叠得到
∴∠C=∠
∵∠1=180°-，∠2=180°-
∴∠1+∠2=180°-+180°-=360°-（+）
∵+=360°-∠C-=360°-36°-36°=288°
∴∠1+∠2=360°-288°=72°
故选：C
【点睛】本题主要考查了折叠问题，掌握三角形的内角和定理，四边形的内角和以及平角的定义是解题的关键．
2．(2023·河南·淮阳第一高级中学七年级期末）如图，已知点，分别在的边，上，将沿折叠，使点落在点的位置，已知，则的度数为（ ）
A．B．C．D．
答案:C
分析由∠A求∠AEF＋∠AFE的大小，由折叠得到∠PEF＋∠PFE的大小，结合平角计算∠1＋∠2．
【详解】解：∵∠A＝70°，
∴∠AEF＋∠AFE＝180°−70°＝110°，
由折叠得：∠PEF＋∠PFE＝∠AEF＋∠AFE＝110°，
∵∠1＋∠PEF＋∠AEF＝180°，∠2＋∠PFE＋∠AFE＝180°，
∴∠1＋∠2＝360°−110°−110°＝140°，
故选：C．
【点睛】本题考查了三角形的内角和、折叠的性质、平角的定义，利用整体思想解题是本题的关键．
3．(2023·全国·八年级课时练习）如图，把纸片沿折叠，使点落在图中的处，若，，则的大小为______.
答案:32°
分析根据折叠性质以及，可知，、、，又∠AED+∠CED=180°，即可求出答案.
【详解】由折叠的性质可知，
又
∴，
根据三角形内角和可得：
∴
故答案为32°.
1．（2012·广东河源·中考真题）如图，在折纸活动中，小明制作了一张△ABC纸片，点D、E分别是边AB、AC上，将△ABC沿着DE折叠压平，A与A′重合，若∠A=75°，则∠1+∠2=【 】
A．150°B．210°C．105°D．75°
答案:A
【详解】翻折变换（折叠问题），三角形内角和定理．
∵△A′DE是△ABC翻折变换而成，∴∠AED=∠A′ED，∠ADE=∠A′DE，∠A=∠A′=75°．
∴∠AED+∠ADE=∠A′ED+∠A′DE=180°﹣75°=105°，∴∠1+∠2=360°﹣2×105°=150°．
故选A．
2．(2023·广东梅州·一模）如图，在△ABC中，点D、E分别为边BC、AC上的点，将△CDE沿DE翻折得到△C′DE，使C′D∥AB．若∠A＝75°，∠C=45°，则∠C′EA的大小为 _____°．
答案:30
分析由C′D∥AB得出∠DGE=∠A=75°，由折叠性质可知，∠C'=∠C=45°，再根据三角形外角性质求出∠C′EA=∠DGE-∠C'=75°-45°=30°．
【详解】解：如图，
∵C′D∥AB，
∴∠DGE=∠A=75°，
由折叠性质可知，∠C'=∠C=45°，
∴∠C′EA=∠DGE-∠C'=75°-45°=30°，
故答案为30．
【点睛】本题考查了翻折变换的知识及三角形外角的性质，解答本题的关键是求出∠DGE的度数是解题的关键．