浙江省2024届中考数学易错模拟卷（二）

这是一份浙江省2024届中考数学易错模拟卷（二），共23页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
一、单选题
1．3的绝对值是（ ）．
A．B．3C．D．
2．下列运算正确的是（ ）
A．a2•a3＝a6B．（﹣a2）3＝﹣a5
C．a10÷a9＝a（a≠0）D．（﹣bc）4÷（﹣bc）2＝﹣b2c2
3．如图，下面的几何体由三个大小相同的小立方块组成，则它的左视图是（ ）
A．B．C．D．
4．若一个三角形三个内角度数的比为1:2:3，那么这个三角形是（ ）
A．直角三角形B．锐角三角形C．钝角三角形D．等边三角形
5．二元一次方程组的解是（ ）
A．B．C．D．
6．一组数据4，5，，7，9的平均数为6，则这组数据的众数为（ ）
A．4B．5C．7D．9
7．不等式组的解集为（ ）
A．x＞B．x＞1C．＜x＜1D．空集
8．下列图形中的五边形ABCDE都是正五边形，则这些图形中的轴对称图形有（ ）
A．1个B．2个C．3个D．4个
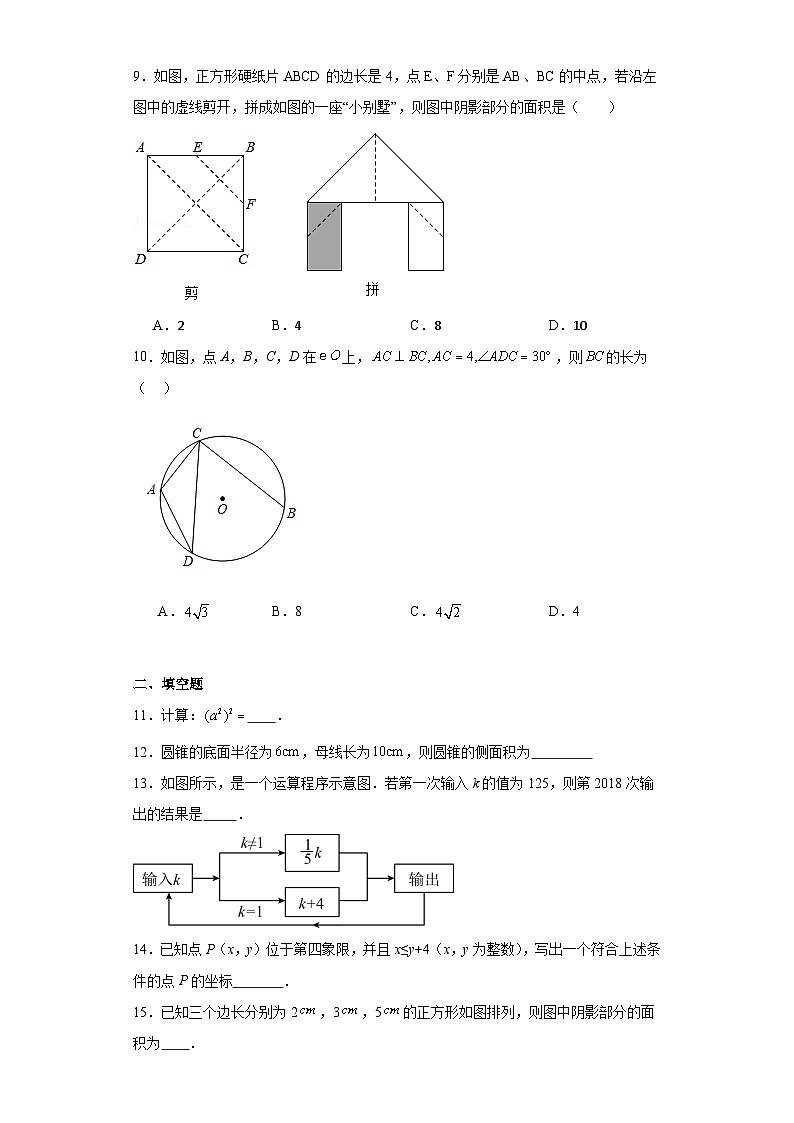
9．如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如图的一座“小别墅”，则图中阴影部分的面积是（ ）
A．2B．4C．8D．10
10．如图，点A，B，C，D在上，，则的长为（ ）
A．B．8C．D．4
二、填空题
11．计算： ．
12．圆锥的底面半径为，母线长为，则圆锥的侧面积为
13．如图所示，是一个运算程序示意图．若第一次输入k的值为125，则第2018次输出的结果是 ．

14．已知点P（x，y）位于第四象限，并且x≤y+4（x，y为整数），写出一个符合上述条件的点P的坐标 ．
15．已知三个边长分别为2，3，5的正方形如图排列，则图中阴影部分的面积为 ．
16．如图，已知正方形ABCD，点M是边BA延长线上的动点（不与点A重合），且AM＜AB，△CBE由平移得到，若过点E作EH⊥AC，H为垂足，则有以下结论：
①点M位置变化，使得∠DHC＝60°时，2BE＝DM；
②无论点M运动到何处，都有DM＝HM；
③在点M的运动过程中，四边形CEMD不可能成为菱形；
④无论点M运动到何处，∠CHM一定大于135°．
以上结论正确的有 （把所有正确结论的序号都填上）．
三、解答题
17．先化简，再求值：，其中.
18．如图，点A．B、C在半径为8的上，过点B作，交延长线于点D．连接，且．

(1)求证：是的切线，
(2)求图中阴影部分的面积．
19．在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践，如图为实践时绘制的截面图．无人机从地面点B垂直起飞到达点A处，测得1号楼顶部E的俯角为67°，测得2号楼顶部F的俯角为40°，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且EC和FD分别垂直地面于点C和D，点B为CD的中点，求2号楼的高度．（结果精确到0.1）（参考数据sin40°≈0.64，cs40°≈0.77，tan40°≈0.84，sin67°≈0.92，cs67°≈0.39，tan67°≈2.36）
20．甲、乙两车分别从两地同时出发，沿同一条公路相向行驶，相遇后，甲车继续以原速行驶到地，乙车立即以原速原路返回到地，甲、乙两车距地的路程与各自行驶的时间之间的关系如图所示．
⑴________，________；
⑵求乙车距地的路程关于的函数解析式，并写出自变量的取值范围；
⑶当甲车到达地时，求乙车距地的路程
21．在一次数学文化课题活动中，把一副数学文化创意扑克牌中的4张扑克牌（如图所示）洗匀后正面向下放在桌面上，从中随机抽取2张牌，请你用列表或画树状图的方法，求抽取的2张牌的数字之和为偶数的概率．
22．如图，在平行四边形ABCD中，点E，F分别在边AB，CD上，且四边形BEDF为正方形．
(1)求证；
(2)已知平行四边形ABCD的面积为，．求的长．
23．如图1，Rt△ABC中，∠ACB=90°，点D为边AC上一点，DE⊥AB于点E，点M为BD中点，CM的延长线交AB于点F
（1）求证：CM=EM；
（2）若∠BAC=50°，求∠EMF的大小；
（3）如图2，若△DAE≌△CEM，点N为CM的中点，求证：AN∥EM
24．如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC
（1）求线段OC的长度；
（2）设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；
（3）在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．
参考答案：
1．B
【分析】根据绝对值的概念进行解答即可．
【详解】解：3的绝对值是3．
故选：B
【点睛】本题考查绝对值的定义，题目简单，掌握绝对值概念是解题关键．
2．C
【分析】根据同底数幂的乘法、除法、积的乘方和幂的乘方进行计算即可．
【详解】解：A、a2•a3＝a5，故A错误；
B、（﹣a2）3＝﹣a6，故B错误；
C、a10÷a9＝a（a≠0），故C正确；
D、（﹣bc）4÷（﹣bc）2＝b2c2，故D错误；
故选：C．
【点睛】本题考查幂的运算，涉及同底数幂的乘法、除法、积的乘方和幂的乘方等知识，是基础考点，掌握相关知识是解题关键．
3．C
【详解】试题分析：根据题意得到几何体的左视图为，故选C．
考点：简单组合体的三视图．
4．A
【分析】根据三角形的内角和度数和内角度数比求出内角判断即可；
【详解】∵三角形三个内角度数的比为1:2:3，
设三个内角的度数分别是，，（k是正整数），
∴，
∴，
∴三角形的三个内角分别是：，，，
∴三角形是直角三角形．
故答案选A．
【点睛】本题主要考查了三角形的性质，准确分析判断是解题的关键．
5．B
【详解】分析：方程组利用加减消元法求出解即可．
详解：，
①+②得：2x=0，
解得：x=0，
把x=0代入①得：y=2，
则方程组的解为，
故选B．
点睛：此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
6．B
【分析】先根据平均数的公式计算出x的值，再求这组数据的众数即可．
【详解】解：∵4，5，，7，9的平均数为6，
∴，
解得：x=5，
∴这组数据为：4，5，5，7，9，
∴这组数据的众数为5．
故选：B．
【点睛】本题考查平均数及众数，熟练掌握平均数、众数的意义是解题的关键．
7．B
【分析】先分别求出不等式组中每一个不等式的解集，然后再取两个不等式的解集的公共部分即可得不等式组的解集．
【详解】解不等式2x>1-x，得：x>，
解不等式x+21，
则不等式组的解集为x>1，
故选B．
【点睛】本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
8．D
【详解】分析：直接利用轴对称图形的性质画出对称轴得出答案．
详解：如图所示：直线l即为各图形的对称轴．
，
故选D．
点睛：此题主要考查了轴对称图形，正确把握轴对称图形的定义是解题关键．
9．B
【详解】解：根据题意，“小别墅”的上面是一个等腰三角形，它的面积是正方形ABCD的一半，而“小别墅”的下面的面积是正方形ABCD的一半，并且下面是两个相等的矩形，
所以图中阴影部分的面积是正方形ABCD面积的
即阴影部分的面积=
考点：正方形
点评：本题考查正方形，解答本题的关键是通过审题，弄清楚阴影部分的面积与正方形面积之间的关系，考生要善于观察
10．A
【分析】连接，根据可得为的直径，又根据得到，故在直角三角形中，利用特殊角的三角函数即可求出．
【详解】解：连接，
，
，
为的直径，
，
，
在中,
，
．.
故选：A．
【点睛】本题主要考查圆周角定理，解三角形，解题的关键是掌握公式、定理。
11．
【分析】根据幂的乘方可进行求解．
【详解】解：；
故答案为．
【点睛】本题主要考查幂的乘方，熟练掌握幂的乘方运算是解题的关键．
12．
【分析】圆锥的侧面积底面半径线长，把相应数值代入即可求解．
【详解】解：圆锥的侧面积．
【点睛】本题考查圆锥侧面积公式的运用，掌握公式是关键．
13．5
【分析】根据运算程序可找出前几次输出的结果，根据输出结果的变化找出变化规律“第2n次输出的结果是5，第2n+1次输出的结果是1（n为正整数）”，依此规律即可得出结论．
【详解】解：∵第1次输出的结果是25，第2次输出的结果是5，第3次输出的结果是1，第4次输出的结果是5，第5次输出的结果是1，…，
∴第2n次输出的结果是5，第2n+1次输出的结果是1（n为正整数），
∴第2018次输出的结果是5．
故答案为：5．
【点睛】本题考查了代数式求值以及规律型中数字的变化类，根据输出结果的变化找出变化规律是解题的关键．
14．（1，-2）（答案不唯一）．
【分析】直接利用第四象限内点的坐标特点得出x，y的取值范围，进而得出答案．
【详解】解：∵点P（x，y）位于第四象限，并且x≤y+4（x，y为整数），
∴x＞0，y＜0，
∴当x=1时，1≤y+4，
解得：0＞y≥-3，
∴y可以为：-2，
故写一个符合上述条件的点P的坐标可以为：（1，-2）（答案不唯一）．
故答案为（1，-2）（答案不唯一）．
【点睛】此题主要考查了点的坐标，正确把握横纵坐标的符号是解题关键．
15．．
【分析】根据相似三角形的性质，利用相似比求出梯形的上底和下底，用面积公式计算即可．
【详解】解：如图，
对角线所分得的三个三角形相似，
根据相似的性质可知，
解得，
即阴影梯形的上底就是（）．
再根据相似的性质可知，
解得：，
所以梯形的下底就是，
所以阴影梯形的面积是．
故答案为．
【点睛】本题考查的是相似三角形的性质，相似三角形的对应边成比例．
16．①②③④
【分析】①正确．证明∠ADM＝30°，即可得出结论．
②正确．证明△DHM是等腰直角三角形即可．
③正确．首先证明四边形CEMD是平行四边形，再证明，DM＞CD即可判断．
④正确．证明∠AHM＜∠BAC＝45°，即可判断．
【详解】解：如图，连接DH，HM．
由题可得，AM＝BE，
∴AB＝EM＝AD，
∵四边形ABCD是正方形，EH⊥AC，
∴EM＝AD，∠AHE＝90°，∠MEH＝∠DAH＝45°＝∠EAH，
∴EH＝AH，
∴△MEH≌△DAH（SAS），
∴∠MHE＝∠DHA，MH＝DH，
∴∠MHD＝∠AHE＝90°，△DHM是等腰直角三角形，
∴DM＝HM，故②正确；
当∠DHC＝60°时，∠ADH＝60°﹣45°＝15°，
∴∠ADM＝45°﹣15°＝30°，
∴Rt△ADM中，DM＝2AM，
即DM＝2BE，故①正确；
∵CD∥EM，EC∥DM，
∴四边形CEMD是平行四边形，
∵DM＞AD，AD＝CD，
∴DM＞CD，
∴四边形CEMD不可能是菱形，故③正确，
∵点M是边BA延长线上的动点（不与点A重合），且AM＜AB，
∴∠AHM＜∠BAC＝45°，
∴∠CHM＞135°，故④正确；
由上可得正确结论的序号为①②③．
故答案为：①②③④．
【点睛】本题考查正方形的性质，全等三角形的判定和性质，等腰直角三角形的判定和性质，直角三角形30度角的性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考填空题中的压轴题．
17．，.
【分析】括号内先通分进行分式的加减法运算，然后再进行分式的乘除法运算，最后把数值代入化简后的结果进行计算即可.
【详解】，
，
，
当时，原式.
【点睛】本题考查了分式的化简求值，熟练掌握分式混合运算的法则是解题的关键.
18．(1)见解析
(2)
【分析】（1）连接，根据圆周角定理求出，根据三角形内角和定理求出，根据切线的判定推出即可．
（2）根据平行线的性质得到，解直角三角形求出，分别求出的面积和扇形的面积，即可得出答案．
【详解】（1）证明：连接，交于，如图所示：

，，
，
，
，
即，
，
，
，
是的切线．
（2）解：，，
，
，，
，
．
【点睛】本题考查了切线的判定定理，圆周角定理，扇形的面积，三角形的面积，解直角三角形等知识点的综合运用，题目比较好，难度适中．
19．45.8米
【分析】通过作辅助线，构造直角三角形，利用直角三角形的边角关系，分别求出EM，AN，进而计算出2号楼的高度DF即可．
【详解】解：过点E、F分别作EM⊥AB，FN⊥AB，垂足分别为M、N，
由题意得，EC＝20，∠AEM＝67°，∠AFN＝40°，CB＝DB＝EM＝FN，AB＝60，
∴AM＝AB﹣MB＝60﹣20＝40，
在Rt△AEM中，
∵tan∠AEM＝，
∴EM＝＝≈16.9，
在Rt△AFN中，
∵tan∠AFN＝，
∴AN＝tan40°×16.9≈14.2，
∴FD＝NB＝AB﹣AN＝60﹣14.2＝45.8，
答：2号楼的高度约为45.8米．
【点睛】本题考查了解直角三角形的应用，构造直角三角形是解题关键．
20．（1）4，120；（2）；（3）乙车距地的路程为.
【分析】（1）观察图像即可解决问题；
（2）运用待定系数法解得即可；
（3）把x=3代入（2）的结论即可．
【详解】解：（1）根据题意可得m=2×2=4，n=280-280÷3.5=120；
故答案为4；120；
（2）设关于的函数解析式为，
因为图像过，
所以，
解得，
所以关于的函数解析式为
设关于的函数解析式为
因为图像过两点
所以
解得：
所以关于的函数解析式为；
（3）当时，，
所以当甲车到达地时，乙车距地的路程为．
【点睛】此题考查的知识点是一次函数的应用，解题的关键是熟练掌握待定系数法确定函数的解析式．
21．．
【详解】试题分析：列出得出所有等可能的情况数，找出抽取2张牌的数字之和为偶数的情况数，即可求出所求的概率．
试题解析：列表如下：
所有等可能的情况数有12种，抽取2张牌的数字之和为偶数的有4种，则P==．
考点：列表法与树状图法；概率及其应用．
22．(1)证明见解析
(2)
【分析】（1）直接根据已知条件证明和全等即可得出答案．
（2）由平行四边形的面积公式求出，然后即可得出答案．
【详解】（1）四边形是正方形，是平行四边形，
，，，
在和中，
，
，
；
（2）由题意可知：，
，
，
，，
由（1）得．
【点睛】本题考查平行四边形的性质、正方形的性质及三角形全等的判定，解题的关键是熟练掌握相关性质并能灵活运用．
23．（1）证明见解析；（2）∠EMF=100°；（3）证明见解析.
【详解】【分析】（1）在Rt△DCB和Rt△DEB中，利用直角三角形斜边中线等于斜边一半进行证明即可得；
（2）根据直角三角形两锐角互余可得∠ABC=40°，根据CM=MB，可得∠MCB=∠CBM，从而可得∠CMD=2∠CBM，继而可得∠CME=2∠CBA=80°，根据邻补角的定义即可求得∠EMF的度数；
（3）由△DAE≌△CEM，CM=EM，∠DEA=90°，结合CM=DM以及已知条件可得△DEM是等边三角形，从而可得∠EDM=60°，∠MBE=30°，继而可得∠ACM=75°，连接AM，结合AE=EM=MB，可推导得出AC=AM，根据N为CM中点，可得AN⊥CM，再根据CM⊥EM，即可得出AN∥EM.
【详解】（1）∵M为BD中点，
Rt△DCB中，MC=BD，
Rt△DEB中，EM=BD，
∴MC=ME；
（2）∵∠BAC=50°，∠ACB=90°，
∴∠ABC=90°-50°=40°，
∵CM=MB，
∴∠MCB=∠CBM，
∴∠CMD=∠MCB+∠CBM=2∠CBM，
同理，∠DME=2∠EBM，
∴∠CME=2∠CBA=80°，
∴∠EMF=180°-80°=100°；
（3）∵△DAE≌△CEM，CM=EM，
∴AE=EM，DE=CM，∠CME=∠DEA=90°，∠ECM=∠ADE，
∵CM=EM，∴AE=ED，∴∠DAE=∠ADE=45°，
∴∠ABC=45°，∠ECM=45°，
又∵CM=ME=BD=DM，
∴DE=EM=DM，
∴△DEM是等边三角形，
∴∠EDM=60°，
∴∠MBE=30°，
∵CM=BM，∴∠BCM=∠CBM，
∵∠MCB+∠ACE=45°，
∠CBM+∠MBE=45°，
∴∠ACE=∠MBE=30°，
∴∠ACM=∠ACE+∠ECM=75°，
连接AM，∵AE=EM=MB，
∴∠MEB=∠EBM=30°，
∠AME=∠MEB=15°，
∵∠CME=90°，
∴∠CMA=90°-15°=75°=∠ACM，
∴AC=AM，
∵N为CM中点，
∴AN⊥CM，
∵CM⊥EM，
∴AN∥CM.
【点睛】本题考查了三角形全等的性质、直角三角形斜边中线的性质、等腰三角形的判定与性质、三角形外角的性质等，综合性较强，正确添加辅助线、灵活应用相关知识是解题的关键.
24．（1）OC=；（2）y=x﹣，抛物线解析式为y=x2﹣x+2；（3）点P存在，坐标为（，﹣）．
【分析】（1）令y=0，求出x的值，确定出A与B坐标，根据已知相似三角形得比例，求出OC的长即可；
（2）根据C为BM的中点，利用直角三角形斜边上的中线等于斜边的一半得到OC=BC，确定出C的坐标，利用待定系数法确定出直线BC解析式，把C坐标代入抛物线求出a的值，确定出二次函数解析式即可；
（3）过P作x轴的垂线，交BM于点Q，设出P与Q的横坐标为x，分别代入抛物线与直线解析式，表示出坐标轴，相减表示出PQ，四边形ACPB面积最大即为三角形BCP面积最大，三角形BCP面积等于PQ与B和C横坐标之差乘积的一半，构造为二次函数，利用二次函数性质求出此时P的坐标即可．
【详解】解：（1）由题可知当y=0时，a（x﹣1）（x﹣3）=0，
解得：x1=1，x2=3，即A（1，0），B（3，0），
∴OA=1，OB=3
∵△OCA∽△OBC，
∴OC：OB=OA：OC，
∴OC2=OA•OB=3，
则OC=；
（2）∵C是BM的中点，即OC为斜边BM的中线，
∴OC=BC，
∴点C的横坐标为，
又OC=，点C在x轴下方，
∴C（，﹣），
设直线BM的解析式为y=kx+b，
把点B（3，0），C（，﹣）代入得： ，
解得：b=﹣，k=，
∴y=x﹣，
又∵点C（，﹣）在抛物线上，代入抛物线解析式，
解得：a=，
∴抛物线解析式为y=x2﹣x+2；
（3）点P存在，
设点P坐标为（x，x2﹣x+2），过点P作PQ⊥x轴交直线BM于点Q，
则Q（x，x﹣），
∴PQ=x﹣﹣（x2﹣x+2）=﹣x2+3x﹣3，
当△BCP面积最大时，四边形ABPC的面积最大，
S△BCP=PQ（3﹣x）+PQ（x﹣）=PQ=﹣x2+x﹣，
当x=﹣时，S△BCP有最大值，四边形ABPC的面积最大，此时点P的坐标为（，﹣）．
【点睛】此题属于二次函数综合题，涉及的知识有：二次函数图象与性质，待定系数法确定函数解析式，相似三角形的判定与性质，以及坐标与图形性质，熟练掌握各自的性质是解本题的关键．