专题67 费马点中三线段模型与最值问题-2024年中考数学重难点专项突破（全国通用）

这是一份专题67 费马点中三线段模型与最值问题-2024年中考数学重难点专项突破（全国通用），文件包含专题67费马点中三线段模型与最值问题原卷版docx、专题67费马点中三线段模型与最值问题解析版docx等2份试卷配套教学资源，其中试卷共16页， 欢迎下载使用。
【模型展示】
问题：在△ABC内找一点P，使得PA+PB+PC最小．
【分析】在之前的最值问题中，我们解决的依据有：两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等．
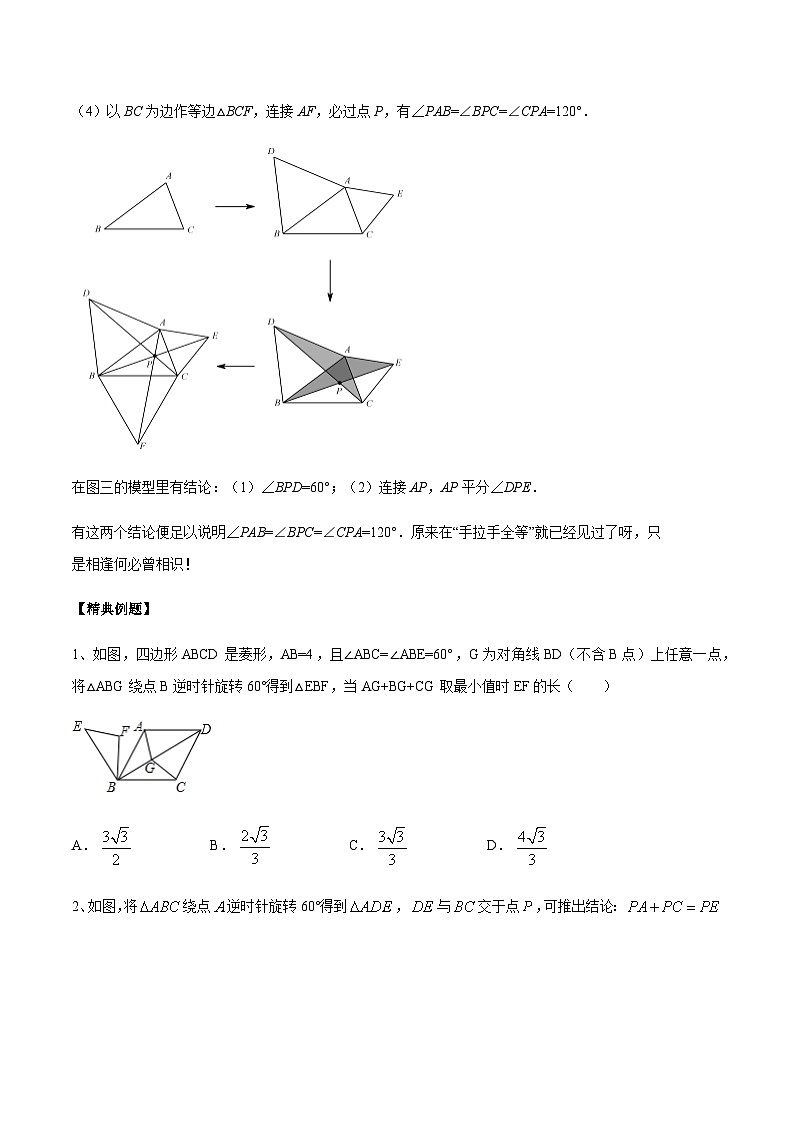
（1）如图，分别以△ABC中的AB、AC为边，作等边△ABD、等边△ACE．
（2）连接CD、BE，即有一组手拉手全等：△ADC≌△ABE．
（3）记CD、BE交点为P，点P即为费马点．（到这一步其实就可以了）
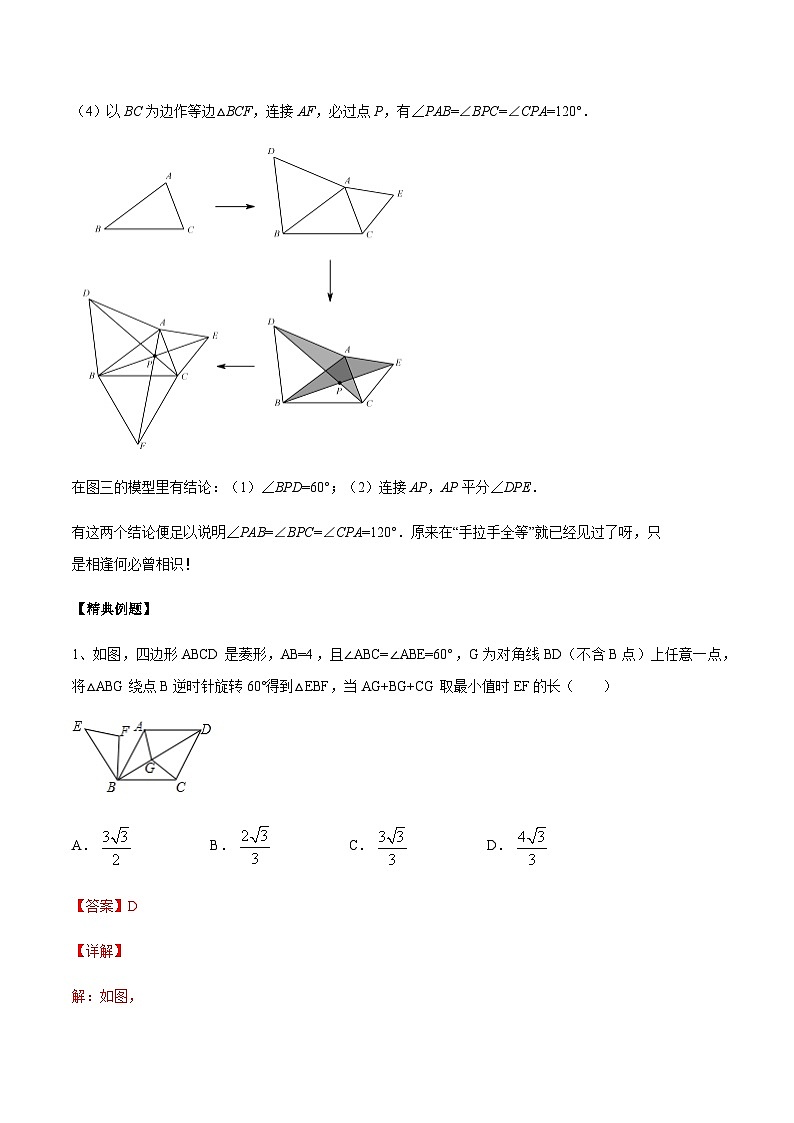
（4）以BC为边作等边△BCF，连接AF，必过点P，有∠PAB=∠BPC=∠CPA=120°．
在图三的模型里有结论：（1）∠BPD=60°；（2）连接AP，AP平分∠DPE．
有这两个结论便足以说明∠PAB=∠BPC=∠CPA=120°．原来在“手拉手全等”就已经见过了呀，只是相逢何必曾相识！
【精典例题】
1、如图，四边形ABCD是菱形，AB=4，且∠ABC=∠ABE=60°，G为对角线BD（不含B点）上任意一点，将△ABG绕点B逆时针旋转60°得到△EBF，当AG+BG+CG取最小值时EF的长（ ）
A．B．C．D．
2、如图，将绕点逆时针旋转60°得到，与交于点，可推出结论：
问题解决：如图，在中，，，．点是内一点，则点到三个顶点的距离和的最小值是___________
3、如图，四边形 是菱形，B=6，且∠ABC=60° ，M是菱形内任一点，连接AM，BM，CM，则AM+BM+CM 的最小值为________．
4、如图，△ABC中，∠BAC＝30°且AB＝AC，P是底边上的高AH上一点．若AP+BP+CP的最小值为2，则BC＝_____．
5、如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.
E
A D
B C
N
M
⑴ 求证：△AMB≌△ENB；
⑵ ①当M点在何处时，AM＋CM的值最小；
②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；
⑶ 当AM＋BM＋CM的最小值为时，求正方形的边长.
6、在正方形ABCD中，点E为对角线AC（不含点A）上任意一点，AB=；
（1）如图1，将△ADE绕点D逆时针旋转90°得到△DCF，连接EF；
①把图形补充完整（无需写画法）； ②求的取值范围；
(2)如图2，求BE+AE+DE的最小值．
费马点”是指位于三角形内且到三角形三个顶点距高之和最短的点。
主要分为两种情况：
（1）当三角形三个内角都小于120°的三角形，通常将某三角形绕点旋转60度，从而将“不等三爪图”中三条线段转化在同一条直线上，利用两点之间线段最短解决问题。
（2）当三角形有一个内角大于120°时，费马点就是此内角的顶点.
费马点问题解题的核心技巧：
旋转60° 构造等边三角形 将“不等三爪图”中三条线段转化至同一直线上 利用两点之间线段最短求解问题