华师大版八年级上册1 平方根课文课件ppt

这是一份华师大版八年级上册1 平方根课文课件ppt，共20页。PPT课件主要包含了问题情景，面积为9则边长为，填一填比一比，平方根的概念，被开方数，负数没有平方根，议一议，答有意义的是，无意义的是，合作探究等内容，欢迎下载使用。
1.我们现已学过哪些运算？2.加法与减法运算之间有什么关系？（加法与减法互逆算）乘法与除法之间有什么关系？3.乘方有没有逆运算？
（加、减、乘、除、乘方五种）
（乘法与除法互逆算。）
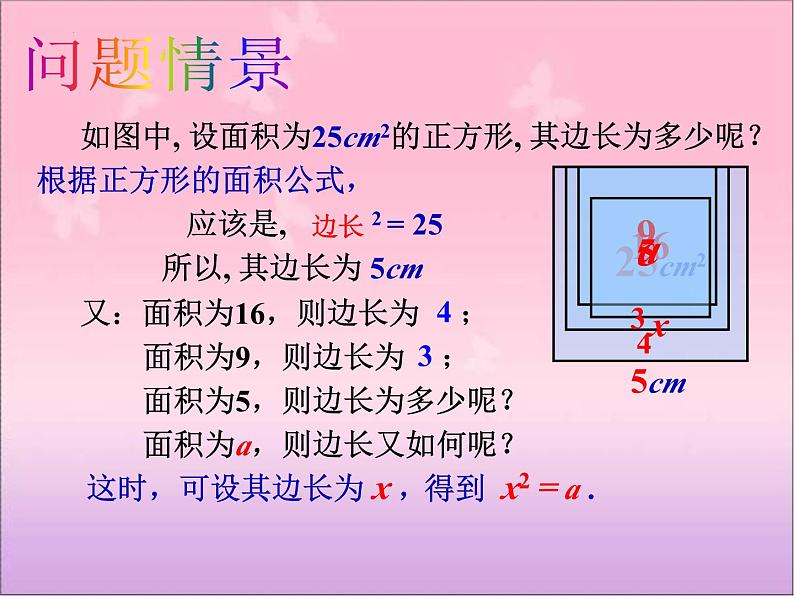
如图中, 设面积为25cm2的正方形, 其边长为多少呢？
应该是, 2 = 25
又：面积为16，则边长为
所以, 其边长为 5cm
面积为5，则边长为多少呢？
面积为a，则边长又如何呢？
根据正方形的面积公式，
这时，可设其边长为 x ，
得到 x2 = a .
12=（ ）22= （ ）32= （ ）42=（ ）52= （ ）62= （ ）72= （ ）82= （ ）92= （ ）102= （ ）
112= （ ）122= （ ）132= （ ）142= （ ）152= （ ）162= （ ）172= （ ）182= （ ）192= （ ）202= （ ）
112= （ 121 ）122= （ 144 ）132= （ 169 ）142= （ 196 ）152= （ 225 ）162= （ 256 ）172= （ 289 ）182= （ 324 ）192= （ 361 ）202= （ 400 ）
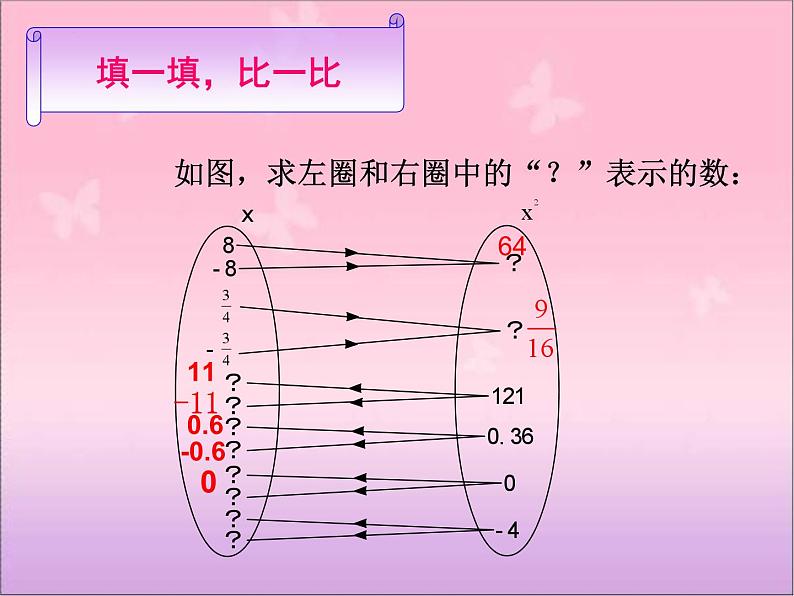
如图，求左圈和右圈中的“？”表示的数：
如果一个数的平方等于a ，那么这个数叫做a 的平方根。例如：52=25所以5是25的一个平方根，（-5）2=52=25，所以-5也是25的一个平方根。
平方根的表示方法、读法
求平方根的写法如下： 正数a的两个平方根可分别写作（正号一般省略），我们可以合并成为读作：正负根号a
例1：求下列数的平方根。
（1）一个正数有几个平方根？（2）0 有几个平方根？（3）负数呢？
一个正数有两个平方根，它们互为相反数；
0只有一个平方根，它是0本身；
特殊：0的算术平方根是0。
一般地，如果一个正数x的平方等于a,即 = a,那么这个正数x叫做a的算术平方根。a的算术平方根记为 ，读作“根号a”，另一个平方根是它的相反数，即 ，因此正数a的平方根可以记作 ，a叫做被开方数。
想一想：负数有算术平方根吗？
例3：求下列各式的值：
1、下列各式中哪些有意义？哪些无意义？为什么？
2、判断（1）5是25的算术平方根；（2）-6是 36 的算术平方根；（3）0的算术平方根是0；（4）0.01是0.1的算术平方根；（5）-5是-25的算术平方根。
① 正数的算术平方根是 数，0的算术平方根 是 ，算术平方根等于它本身的数是
② 的算术平方根是
+1-1+2-2+3-3
X x2
x2 X
求一个数a的平方根的运算，叫做开平方.
开平方与平方是什么关系？
2、一个正数有两个平方根，0只有一个平方根，它是0本 身；负数没有平方根。
3、求一个数a的平方根的运算，叫做开平方，其中a叫做 被开方数。
4、平方与开平方互为逆运算。
1、 一般地，如果一个数X的平方等于a，即X2=a那么这个 数X叫做a的平方根（也叫做二次方根）。