


- 【讲通练透】重难点突破03 原函数与导函数混合还原问题 (十三大题型)-2024年高考数学重难点突破精讲 试卷 2 次下载
- 【讲通练透】重难点突破03 最全归纳平面向量中的范围与最值问题 (十大题型)-2024年高考数学重难点突破精讲 试卷 2 次下载
- 【讲通练透】重难点突破04 三次函数的图象和性质 (七大题型)-2024年高考数学重难点突破精讲 试卷 2 次下载
- 【讲通练透】重难点突破05 极值点偏移问题与拐点偏移问题(七大题型)-2024年高考数学重难点突破精讲 试卷 2 次下载
- 【讲通练透】重难点突破05 立体几何中的常考压轴小题(七大题型)-2024年高考数学重难点突破精讲 试卷 3 次下载
【讲通练透】重难点突破04 立体几何中的轨迹问题(六大题型)-2024年高考数学重难点突破精讲
展开2、精练习题。复习时不要搞“题海战术”,应在老师的指导下,选一些源于课本的变式题,或体现基本概念、基本方法的基本题,通过解题来提高思维能力和解题技巧,加深对所学知识的深入理解。在解题时,要独立思考,一题多思,一题多解,反复玩味,悟出道理。
3、加强审题的规范性。每每大考过后,总有同学抱怨没考好,纠其原因是考试时没有注意审题。审题决定了成功与否,不解决这个问题势必影响到高考的成败。那么怎么审题呢? 应找出题目中的已知条件 ;善于挖掘题目中的隐含条件 ;认真分析条件与目标的联系,确定解题思路 。
4、重视错题。错误是最好的老师”,但更重要的是寻找错因,及时进行总结,三五个字,一两句话都行,言简意赅,切中要害,以利于吸取教训,力求相同的错误不犯第二次。
重难点突破04 立体几何中的轨迹问题
目录
立体几何中的轨迹问题常用的五种方法总结:
1、定义法
2、交轨法
3、几何法
4、坐标法
5、向量法
题型一:由动点保持平行求轨迹
例1.(2023·贵州铜仁·高二贵州省铜仁第一中学校考开学考试)设正方体的棱长为1,点E是棱的中点,点M在正方体的表面上运动,则下列命题:
①如果,则点M的轨迹所围成图形的面积为;
②如果∥平面,则点M的轨迹所围成图形的周长为;
③如果∥平面,则点M的轨迹所围成图形的周长为;
④如果,则点M的轨迹所围成图形的面积为.
其中正确的命题个数为( )
A.1B.2C.3D.4
【答案】C
【解析】由面,而面,则,又,
又,面,则面,
由面,则,同理,
,面,则面,
所以垂直于面所有直线,且面,
若,则在边长为的正△的边上,
故轨迹图形面积为,①对;
若分别为中点,连接,
由正方体的性质易得,,
所以共面,且为平行四边形,故面即为面,
由面,面,则面,
同理可得面,,面,
所以面面,要使∥平面,则在△的边上,
所以轨迹长为,②错;
若分别为的中点,连接,显然,
所以共面,即面,
由,面,面,则面,
又,同理可得面,,面,
所以面面,故面内任意直线都与面平行,
要使∥平面,则在四边形的边上运动,
此时轨迹长为,③对;
若分别是的中点,并依次连接,
易知为正六边形,显然,,
由面,面,则面,同理可得面,
,面,所以面面,
由面,则面,故垂直于面所有直线,
要使,则在边长为的正六边形边上运动,
所以轨迹图形面积为,④对;
故选:C
例2.(2023·辽宁沈阳·高一沈阳二十中校联考期末)在棱长为1的正方体中,E在棱上且满足,点F是侧面上的动点,且面AEC,则动点F在侧面上的轨迹长度为 .
【答案】
【解析】如图,取的中点,并连接、、,
因为E在棱上且满足,即E是棱的中点,
所以,又平面,平面,
所以平面,同理可证平面,
又,所以平面平面,又平面,
所以平面,所以动点F在侧面上的轨迹即为,
因为正方体的棱长为1,由勾股定理有:.
故答案为:.
例3.(2023·福建福州·高一福建省福州屏东中学校考期末)如图所示,在棱长为2的正方体中,E,F,G分别为所在棱的中点,P为平面内(包括边界)一动点,且∥平面EFG,则P点的轨迹长度为
【答案】2
【解析】因为∥,则四点共面,
连接,
因为E,F分别为所在棱的中点,则∥,
且平面FGE,平面FGE,所以∥平面FGE,
因为F,G分别为所在棱的中点,则∥,
且平面FGE,平面FGE,所以∥平面FGE,
,平面,
所以平面FGE∥平面,且平面平面,
可得当且仅当点P在棱BC上时,即平面,满足∥平面EFG,
所以点P的轨迹为线段BC,长度为2.
故答案为:2.
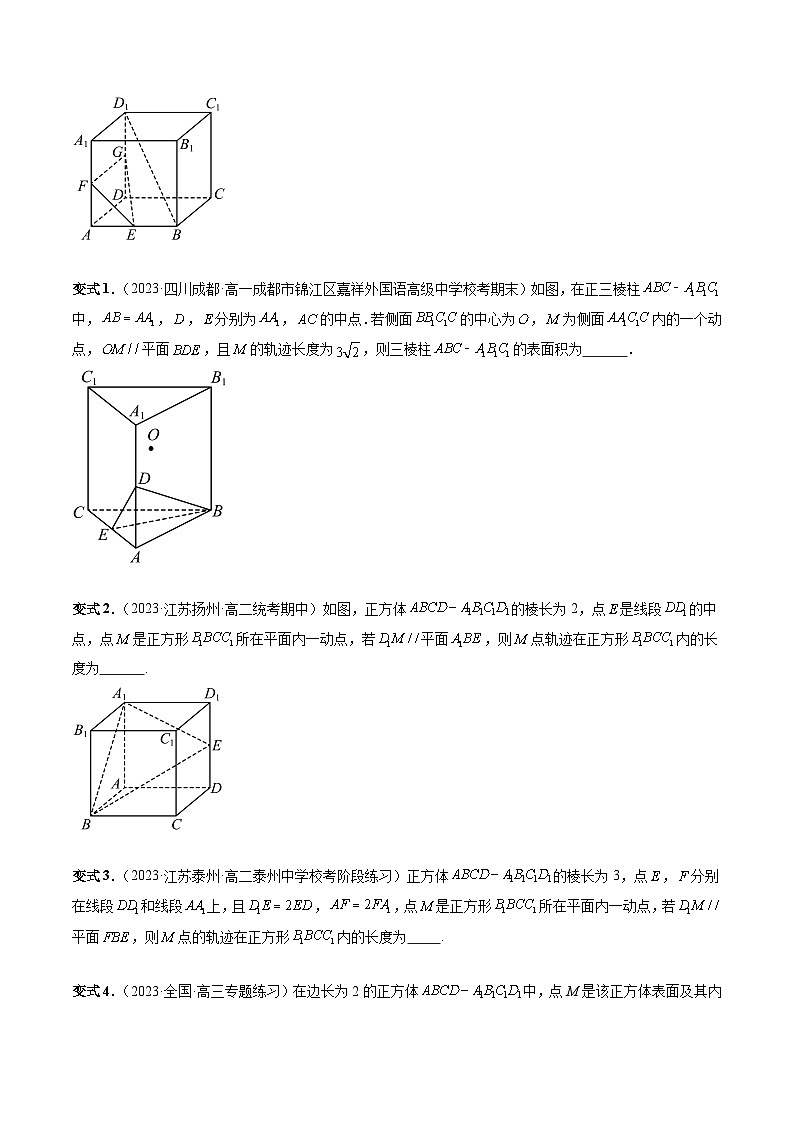
变式1.(2023·四川成都·高一成都市锦江区嘉祥外国语高级中学校考期末)如图,在正三棱柱中,,,分别为,的中点.若侧面的中心为,为侧面内的一个动点,平面,且的轨迹长度为,则三棱柱的表面积为 .
【答案】/
【解析】
连接交于,取的中点,过作,
分别交于,连接,
易得,
因为平面,平面,所以平面,
平面,因为,且都在面内,所以平面平面,
所以的轨迹为线段,
因为,所以,
因为,所以,
所以,
故三棱柱的表面积为.
故答案为:.
变式2.(2023·江苏扬州·高二统考期中)如图,正方体的棱长为2,点是线段的中点,点是正方形所在平面内一动点,若平面,则点轨迹在正方形内的长度为 .
【答案】
【解析】取的中点,连接,如图所示:
因为,平面,平面,所以平面.
因为,平面,平面,所以平面.
又因为平面,,
所以平面平面.
因为平面,平面,
所以点在平面的轨迹为.
所以.
故答案为:
变式3.(2023·江苏泰州·高二泰州中学校考阶段练习)正方体的棱长为3,点,分别在线段和线段上,且,,点是正方形所在平面内一动点,若平面,则点的轨迹在正方形内的长度为 .
【答案】
【解析】
如图,在上取点,使得,在上取点,使得,连接.
根据正方体的性质可知,,.
由已知可得,,
又,所以.
又,所以,四边形为平行四边形,
所以,,且.
同理可得,,且,.
根据正方体的性质可知,,且,
所以,,且,
所以,四边形是平行四边形,
所以,.
因为平面,平面,所以平面.
同理可得,平面.
因为平面,平面,,
所以,平面平面.
又平面平面,
所以,根据面面平行的性质定理可知,只有在线段上运动时,满足条件.
过点作,垂足为,
易知,且,,
所以,.
故答案为:.
变式4.(2023·全国·高三专题练习)在边长为2的正方体中,点M是该正方体表面及其内部的一动点,且平面,则动点M的轨迹所形成区域的面积是 .
【答案】
【解析】如图,边长为2的正方体中,
动点M满足平面,
由面面平行的性质得:当始终在一个与平面平行的面内,即满足题意,
连接,,,
因为且,所以四边形为平行四边形,
所以,同理,
又平面,平面,所以平面,
因为平面,平面,所以平面,
又因平面,
所以平面平面,
又平面,所以动点M的轨迹所形成区域为,
,
,
所以动点M的轨迹所形成区域的面积是.
故答案为:.
变式5.(2023·全国·高三专题练习)如图,已知正方体的棱长为分别是棱的中点,点为底面四边形内(包括边界)的一动点,若直线与平面无公共点,则点在四边形内运动所形成轨迹的长度为 .
【答案】
【解析】取的中点,连接,如图所示:
分别是棱的中点,所以,
又因为平面平面,所以平面.
因为,
所以四边形为平行四边形,所以.
又因为平面平面,所以平面.
因为,所以平面平面.
因为点为底面四边形内(包括边界)的一动点,直线与平面无公共点,
所以的轨迹为线段,则.
故答案为:.
变式6.(2023·全国·高三专题练习)如图所示,正方体的棱长为分别为,的中点,点是正方体表面上的动点,若平面,则点在正方体表面上运动所形成的轨迹长度为 .
【答案】/
【解析】取的中点的中点,连结.正方体
的棱长为2.为中点,所以,
所以且.
因为为分别为的中点,
所以,且,所以四边形为平行四边形,
所以.
因为面面,
所以面.
同理可证:面.
又面面,
所以面面.
所以点在正方体表面上运动所形成的轨迹为三角形.
因为正方体的棱长为2,所以,
所以三角形的周长为.
故答案为:.
变式7.(2023·全国·高三专题练习)已知棱长为的正四面体,为的中点,动点满足,平面经过点,且平面平面,则平面截点的轨迹所形成的图形的周长为 .
【答案】
【解析】设的外心为,的中点为,过作的平行线,则以为坐标原点,可建立如图所示空间直角坐标系,
为等边三角形,,,,
,,,
设,由得:,
整理可得:,
动点的轨迹是以为球心,为半径的球;
延长到点,使得,,,
则,,又平面,平面,
平面,平面,由,平面,
平面平面,即平面为平面,
则点到平面的距离即为点到直线的距离,
,,,即,
点到直线的距离,
截面圆的半径,球被平面截得的截面圆周长为,
即平面截点的轨迹所形成的图形的周长为.
故答案为:.
题型二:由动点保持垂直求轨迹
例4.(2023·湖南株洲·高三株洲二中校考阶段练习)在棱长为4的正方体中,点P、Q分别是,的中点,点M为正方体表面上一动点,若MP与CQ垂直,则点M所构成的轨迹的周长为 .
【答案】
【解析】如图,只需过点P作直线CQ的垂面即可,垂面与正方体表面的交线即为动点M的轨迹.
分别取,的中点R,S,
由,知,易知,
又,,平面ABRS,
所以平面ABRS,
过P作平面ABRS的平行平面,点M的轨迹为四边形,
其周长与四边形ABRS的周长相等,
其中,,
所以点M所构成的轨迹的周长为.
故答案为:
例5.(2023·湖南长沙·长郡中学校考二模)在正四棱柱中,,E为中点,为正四棱柱表面上一点,且,则点的轨迹的长为 .
【答案】/
【解析】如图,连接,,由题可知,,平面.
因平面,则.
又平面,平,,则平面.又平面,则;
如图,过E做平行线,交于F,则F为中点.连接,
过做垂线,交于G.
由题可得,平面,又,则平面.
因平面,则.
又平面,平面,,则平面.
因平面,则;
因平面,平面,,则平面.
连接,则点P轨迹为平面与四棱柱的交线,即.
注意到,
,则,故.
则点的轨迹的长为.
故答案为:.
例6.(2023·全国·唐山市第十一中学校考模拟预测)已知为正方体的内切球球面上的动点,为的中点,,若动点的轨迹长度为,则正方体的体积是 .
【答案】
【解析】如图所示:
正方体,设,则内切球的半径,
其中为的中点,取的中点,连接,
则有:,
又,平面,
所以平面,
所以动点的轨迹是平面截内切球的交线,
即平面截内切球的交线,
因为正方体,,
如图所示:
连接,则有且,
,且,
设到平面的距离为:,
则在三棱锥中,有,
所以,
即,
解得:,
截面圆的半径,
所以动点的轨迹长度为:,
即,解得,
所以,正方体的体积:,
故答案为:.
变式8.(2023·全国·高三专题练习)已知直三棱柱的所有棱长均为4,空间内的点满足,且,则满足条件的所形成曲线的轨迹的长度为 .
【答案】/
【解析】设的中点为,的中点为,易知,
因为,且,所以点在以,为直径的球上,
球心分别为,,半径分别为,,即,,
又,所以,即,
过作,垂足为,则,
因为两球的交线为圆,所以点轨迹是以为圆心,以为半径的圆,
所以轨迹长度为.
故答案为:.
变式9.(2023·四川成都·三模)如图,AB为圆柱下底面圆O的直径,C是下底面圆周上一点,已知,,圆柱的高为5.若点D在圆柱表面上运动,且满足,则点D的轨迹所围成图形的面积为 .
【答案】10
【解析】作母线,,连接,
因为,所以共面,是圆柱的一个截面,
平面,平面,所以,
又由已知得,而,平面,
所以平面,
由得,所以平面,
矩形即为点轨迹,
,则,又,
所以矩形的面积为.
故答案为:10.
变式10.(2023·全国·高三专题练习)如图,为圆柱下底面圆的直径,是下底面圆周上一点,已知,圆柱的高为5.若点在圆柱表面上运动,且满足,则点的轨迹所围成图形的面积为 .
【答案】10
【解析】因为是圆柱下底面圆的直径,所以,
又,,平面,所以平面,
设过的母线与上底面的交点为,过的母线与上底面的交点为,连,
因为平面,平面,所以,
因为,平面,所以平面,
所以点在平面内,又点在圆柱的表面,所以点的轨迹是矩形,
依题意得,,,所以,
所以矩形的面积为.
故点的轨迹所围成图形的面积为.
故答案为:.
变式11.(2023·浙江宁波·高一慈溪中学校联考期末)如图,在直三棱柱中,,,,动点在内(包括边界上),且始终满足,则动点的轨迹长度是 .
【答案】
【解析】在直三棱柱中,平面,
因为平面,所以,,
又因为,,、平面,
所以,平面,
因为平面,所以,,
因为,,则四边形为菱形,所以,,
又因为,、平面,所以,平面,
因为平面,所以,.
在平面内,过点作,垂足为点,
因为平面,平面,则,
因为,,、平面,
所以,平面,
因为平面,则,
因为,、平面,所以,平面,
由于动点又在内,所以动点在平面与平面的交线上,
因为,,,
所以,,
由等面积法可得,
因此,动点的轨迹长度是.
故答案为:.
变式12.(2023·山东枣庄·高一统考期末),分别是棱长为1的正方体的棱的中点,点在正方体的表面上运动,总有,则点的轨迹所围成图形的面积为 .
【答案】
【解析】取中点,连接,设,
则,,,
所以,
所以,
因为,
所以,
所以,即,
因为正方体中面,面,
所以,
因为面,,
所以面,
因为正方体中面,面,
所以,
所以点的轨迹为矩形,
在直角中,
所以矩形面积为.
即点的轨迹所围成图形的面积为.
故答案为:
变式13.(2023·四川广元·高二广元中学校考期中)如图,为圆柱下底面圆的直径,是下底面圆周上一点,已知,,圆柱的高为5.若点在圆柱表面上运动,且满足,则点的轨迹所围成图形的面积为 .
【答案】
【解析】因为是圆柱下底面圆的直径,
所以,
又,,,平面,
所以平面,
设过A的母线与上底面的交点为,过的母线与上底面的交点为,连,,,
则四边形为矩形,
因为平面,平面,
所以,
因为,,平面,
所以平面,
所以点在平面内,
又点在圆柱的表面,
所以点的轨迹所围成图形是矩形,
依题意得,,,
所以,
所以矩形的面积为,
故点的轨迹所围成图形的面积为.
故答案为:.
变式14.(2023·陕西榆林·高二校考阶段练习)如图,正方体的棱长为,点是棱的中点,点是正方体表面上的动点.若,则点在正方体表面上运动所形成的轨迹的长度为( )
A.B.
C.D.
【答案】C
【解析】取的中点,的中点,连接、、、、,
设,如下图所示.
因为四边形是正方形,又点是棱的中点,点是的中点,
则,,,
所以,,所以,,
所以,,
所以,,即.
在正方体中,平面,
又平面,所以,
又,、平面,所以平面,
又平面,所以,同理可得,,
又,、平面,所以,平面.
所以点在正方体表面上运动所形成的轨迹为的三边,
因为正方体的棱长为,
由勾股定理可得,同理可得,,
所以的周长为.
故选:C.
题型三:由动点保持等距(或定长)求轨迹
例7.(2023·贵州贵阳·高三贵阳一中校考期末)在棱长为1的正方体中,点Q为侧面内一动点(含边界),若,则点Q的轨迹长度为 .
【答案】/
【解析】由题意,在面的轨迹是以为圆心,半径为的四分之一圆弧,
所以轨迹长度为.
故答案为:
例8.(2023·湖北武汉·高一湖北省水果湖高级中学校联考期末)已知正方体的棱长为3,动点在内,满足,则点的轨迹长度为 .
【答案】
【解析】在正方体中,如图,
平面,平面,则,而,
,,平面,于是平面,又平面,
则,同理,而,,平面,
因此平面,令交平面于点,
由,得,
即,解得,
而,于是,
因为点在内,满足,则,
因此点的轨迹是以点为圆心,为半径的圆在内的圆弧,
而为正三角形,则三棱锥必为正三棱锥,为正的中心,
于是正的内切圆半径,
则,即,,
所以圆在内的圆弧为圆周长的,
即点的轨迹长度为
故答案为:
例9.(2023·河北邯郸·高一大名县第一中学校考阶段练习)已知正方体的棱长为1,点P在该正方体的表面上运动,且则点P的轨迹长度是 .
【答案】
【解析】当时,如图,点的轨迹是在面,,三个面内以1为半径,圆心角为的三段弧,所以此时点点P在该正方体的表面上运动的轨迹的长度为,
故答案为:
变式15.(2023·贵州铜仁·统考模拟预测)已知正方体的棱长为4,点P在该正方体的表面上运动,且,则点P的轨迹长度是 .
【答案】
【解析】因为,所以点可能在平面内,可能在平面内,可能在平面内.
当点在平面内时,
由平面,平面,可知,
所以,所以,
所以点到的距离为,
所以点的轨迹为以点为圆心,为半径的圆与正方形边界及其内部的交线.
如上图,,,
则的长,
所以,当点在平面内时,点P的轨迹长度是.
同理可得,当点在平面内时,点P的轨迹长度也是.
当点在平面时,点P的轨迹长度也是.
综上所述,点P的轨迹长度为.
故答案为:.
变式16.(2023·黑龙江齐齐哈尔·统考二模)表面积为36π的球M表面上有A,B两点,且为等边三角形,空间中的动点P满足,当点P在所在的平面内运动时,点P的轨迹是 ;当P在该球的球面上运动时,点P的轨迹长度为 .
【答案】圆
【解析】设球的半径为r,则,解得r=3,
在平面内,动点P的轨迹组成一个圆,以线段AB所在直线为x轴,以靠近点B且长度为1处为坐标原点,
则,,此时动点P的轨迹方程为,
设其圆心为,则在空间中,z轴和xOy坐标平面垂直,
动点P的轨迹为xOy平面中的圆绕x轴旋转一周形成球的球面,
如图所示,
所以点P的轨迹是两个球面的交线,这两个球分别是以M和为球心,
在中,结合余弦定理得到.
设交线所围成的圆半径为R.则,
解得.所以交线的长度为.
故答案为:圆;
变式17.(2023·全国·高三专题练习)已知正四棱柱的体积为16,是棱的中点,是侧棱上的动点,直线交平面于点,则动点的轨迹长度的最小值为 .
【答案】
【解析】如图取的中点,连接交于点,连接、交于点,连接、,
因为是棱的中点,所以,则为的四等分点且,
由正四棱柱的性质可知且,所以四边形为平行四边形,所以,
所以,所以、、、四点共面,
所以平面平面,
连接交于点,因为是侧棱上的动点,直线交平面于点,
所以线段即为点的轨迹,
如图在平面中,过点作,交于点,因为,
所以,所以,所以,
设、,,
依题意,,
所以,
要求动点的轨迹长度的最小值,即求的最小值,即求的最小值,
因为,所以,
所以,
当且仅当,即、时取等号,
所以,所以,即动点的轨迹长度的最小值为.
故答案为:
变式18.(2023·全国·高三专题练习)已知棱长为8的正方体中,平面ABCD内一点E满足,点P为正方体表面一动点,且满足,则动点P运动的轨迹周长为 .
【答案】
【解析】,则在的延长线上,且,
由正方体性质知平面,当在平面上时,平面,,由得,因此点轨迹是以为圆心,2为半径的圆在正方形内的部分即圆周的,弧长为,从而知点在以为顶点的三个面内.
当在棱上时,,,
因此点在面时,点轨迹是以为圆心,为半径的圆在正方形内的圆弧,圆弧的圆心角为,弧长为,同理点在面内的轨迹长度也为,
所以所求轨迹长度为.
故答案为:.
变式19.(2023·全国·高三专题练习)如图,已知棱长为2的正方体A′B′C′D′-ABCD,M是正方形BB′C′C的中心,P是△A′C′D内(包括边界)的动点,满足PM=PD,则点P的轨迹长度为 .
【答案】
【解析】如图建立空间直角坐标系,则
设平面的法向量
则有,令,则
则
设,则
∵,则
又∵PM=PD,则
整理得:
联立方程,则
可得,可得
当时,,当时,
在空间中,满足PM=PD的P为过MD的中点且与MD垂直的平面
两个平面的公共部分为直线,即点P的轨迹为平面A′C′D,则
故答案为:.
变式20.(2023·河南许昌·高三统考阶段练习)三棱锥的体积为,底面三角形是边长为的正三角形且其中心为,三棱锥的外接球球心到底面的距离为2,则点的轨迹长度为 .
【答案】
【解析】三棱锥的体积为,底面三角形是边长为的正三角形,
设三棱锥的高为
所以,故,
又正三角形的外接圆半径为,则,
又三棱锥的外接球球心到底面的距离为2,
所以三棱锥的外接球半径,即,
又因为顶点到底面的距离为,
所以顶点的轨迹是一个截面圆的圆周(球心在底面和截面圆之间)且球心到该截面圆的距离为,
所以截面圆的半径为,
故顶点的轨迹长度是.
故答案为:.
变式21.(2023·全国·高三专题练习)在三棱锥中,,二面角的大小为,在侧面内(含边界)有一动点,满足到的距离与到平面的距离相等,则动点的轨迹的长度为 .
【答案】
【解析】如图,过作于,平面于,
过作于,连接,
则为二面角的平面角,
由,
得.
又,所以,
在中,以所在直线为轴,所在直线为轴建立平面直角坐标系,
则直线的方程为,
直线的方程为,
所以直线与的交点坐标为,
所以的轨迹为线段,
长度为.
故答案为:.
题型四:由动点保持等角(或定角)求轨迹
例10.(2023·山东·高三专题练习)如图所示,在平行四边形中,E为中点,,,.沿着将折起,使A到达点的位置,且平面平面.设P为内的动点,若,则P的轨迹的长度为 .
【答案】
【解析】
建立如图示空间直角坐标系,
则,
设
则
∴\
,
∵∴,
∴
整理化简得:
∴P的轨迹为圆,交于,于,
则
∴所对应的圆心角,∴弧长为.
故答案为:.
例11.(2023·全国·高三专题练习)在棱长为6的正方体中,点是线段的中点,是正方形(包括边界)上运动,且满足,则点的轨迹周长为 .
【答案】/
【解析】如图,在棱长为6的正方体中,
则平面,平面,
又,在平面上,,,
又,,
,即,
如图,在平面中,以为原点,分别为轴建立平面直角坐标系,
则,,,
由,知,
化简整理得,,圆心,半径的圆,
所以点的轨迹为圆与四边形的交点,即为图中的
其中,,,则
由弧长公式知
故答案为:.
例12.(2023·湖北省直辖县级单位·统考模拟预测)已知正方体的棱长为2,M为棱的中点,N为底面正方形ABCD上一动点,且直线MN与底面ABCD所成的角为,则动点N的轨迹的长度为 .
【答案】
【解析】如图所示,取BC中点G,连接MG,NG,由正方体的特征可知MG⊥底面ABCD,
故MN与底面ABCD的夹角即,
∴,则,
故N点在以G为原点为半径的圆上,又N在底面正方形ABCD上,
即N的轨迹为图示中的圆弧,
易知,
所以长为.
故答案为:.
变式22.(2023·陕西·高三陕西省榆林中学校联考阶段练习)已知正方体的棱长为2,点为平面内的动点,设直线与平面所成的角为,若,则点的轨迹所围成的周长为 .
【答案】
【解析】如图所示,连接交平面于,连接,
因为平面,所以,又,且与相交,
所以平面,所以,
同理可得,又,
所以平面,
∴是平面所成的角,∴.
由可得,,即.
在四面体中,,平面,
所以,所以为的中心,
又,.∴四面体为正三棱锥,
如图所示:在等边三角形中,,
,
∵,∴,即在平面内的轨迹是以为圆心,半径为的圆,∴周长为.
故答案为:
变式23.(2023·全国·高三专题练习)已知点P是棱长为2的正方体的表面上一个动点,若使的点P的轨迹长度为a;使直线平面BDC的点P的轨迹长度为b;使直线AP与平面ABCD所成的角为45°的点P的轨迹长度为c.则a,b,c的大小关系为 .(用“<”符号连接)
【答案】b<c<a
【解析】若点到点的距离为2,则点的轨迹为球的表面与正方体交轨,
在平面内,的轨迹为以为圆心,2为半径的圆弧,
由对称性知,这样的圆弧同样在平面内和平面内,故的轨迹长度;
若平面,则点的轨迹为过点且平行于平面的平面与正方体交轨,
而平面平面,所以点的轨迹长度为三角形的周长(除掉点,不影响周长),故,
若直线与平面所成的角为,则点的轨迹为圆锥的侧面与正方体交轨,
在平面内,点的轨迹为对角线(除掉点,不影响);
在平面内,点的轨迹为对角线(除掉点,不影响);
在平面内是以点为圆心2为半径的圆弧,如图,
故点的轨迹长度为,
∵,∴,即.
故答案为:.
变式24.(2023·全国·高三专题练习)已知正方体中,,点E为平面内的动点,设直线与平面所成的角为,若,则点E的轨迹所围成的面积为 .
【答案】
【解析】如图所示,连接交平面于,连接,
由题意可知平面,
所以是与平面所成的角,
所以=.
由可得,即.
在四面体中,,,
所以四面体为正三棱锥,为的重心,
如图所示:
所以解得,,
又因为,
所以,
即在平面内的轨迹是以O为圆心,半径为1的圆,
所以.
故答案为:.
变式25.(2023·山西大同·高一统考期中)已知是半径为2的球面上的四点,且.二面角的大小为,则点形成的轨迹长度为 .
【答案】
【解析】由题意,为等腰直角三角形,且外接圆半径,圆心为中点,
又外接球半径,球心,则,
易知:为等腰直角三角形,又二面角的大小为,
由为外接圆直径,且面面,则与面所成角为,
所以到外接圆圆心距离,故外接圆的半径为,
注意:根据二面角大小及球体的对称性,如上图示,
轨迹在大球冠对应外接圆优弧的一侧,在小球冠对应外接圆劣弧的一侧,
所以轨迹长度为.
故答案为:
变式26.(2023·贵州铜仁·高二统考期末)粽子是端午节期间不可缺少的传统美食,铜仁的粽子不仅馅料丰富多样,形状也是五花八门,有竹筒形、长方体形、圆锥形等,但最常见的还是“四角粽子”,其外形近似于正三棱锥.因为将粽子包成这样形状,既可以节约原料,又不失饱满,而且十分美观.如图,假设一个粽子的外形是正三棱锥,其侧棱和底面边长分别是8cm和6cm,是顶点在底面上的射影.若是底面内的动点,且直线与底面所成角的正切值为,则动点的轨迹长为 .
【答案】
【解析】由题意可知是底面等边三角形的的中心,所以,
进而,
连接,由于底面,所以即为直线与底面所成的角,所以,
因此点在以为圆心,半径为的圆上运动,所以的轨迹长为,
故答案为:
变式27.(2023·广东佛山·高二校联考期中)如图,正方体的棱长为1,点P为正方形内的动点,满足直线BP与下底面ABCD所成角为的点P的轨迹长度为( )
A.B.C.D.
【答案】B
【解析】直线BP与下底面ABCD所成角等于直线BP与上底面所成角,
连接,因为⊥平面,平面,
所以⊥,故为直线BP与上底面所成角,
则,
因为,所以,
故点P的轨迹为以为圆心,为半径,位于平面内的圆的,
故轨迹长度为.
故选:B
变式28.在正方体中,动点M在底面内运动且满足,则动点M在底面内的轨迹为( )
A.圆的一部分B.椭圆的一部分
C.双曲线一支的一部分D.前三个答案都不对
【答案】A
【解析】因为,故在圆锥面上,该圆锥以为轴,为顶点,
而M在底面内,
故动点M在底面内的轨迹是以D为圆心的四分之一圆弧.
故选:A.
题型五:投影求轨迹
例13.(2023·安徽滁州·高三校考阶段练习)如图,在中,,,,D为线段BC(端点除外)上一动点.现将沿线段AD折起至,使二面角的大小为120°,则在点D的移动过程中,下列说法错误的是( )
A.不存在点,使得
B.点在平面上的投影轨迹是一段圆弧
C.与平面所成角的余弦值的取值范围是
D.线段的最小值是
【答案】D
【解析】过点B作AD的垂线,交AD于点E,连接,,过点作BE的垂线,交BE于点H,易知,则平面,所以为二面角的平面角的补角,即,所以,即H为BE的中点,易知平面平面,又,所以平面ABC,所以在平面ABC上的投影为点H,
对于选项A,若,连接CH,则,而这是不可能成立的,故A正确;
对于选项B,因为,所以点E的轨迹为以AB为直径的一段圆弧,又H为BE的中点,所以点H的轨迹也为一段圆弧,故B正确;
对于选项C,连接AH,则与平面ABC所成的角为,设,则,所以由,得,所以,所以,所以,所以,故C正确;
对于选项D,设,则,,
,
其中,故,故D错误,
故选:D
例14.(2023·江苏徐州·高二徐州市第一中学校考阶段练习)如图,在等腰中,,,为的中点,为的中点,为线段上一个动点(异于两端点),沿翻折至,点在平面上的投影为点,当点在线段上运动时,以下说法不正确的是( ).
A.线段为定长B.
C.D.点的轨迹是圆弧
【答案】B
【解析】翻折后的立体图形,如图所示.
对A,因为点在平面上的投影为点,所以平面,
又平面,所以,
故为直角三角形,又为斜边的中点,
所以为定长.
故A正确.
对C,当在处时,此时点在平面上的投影为点与重合,故,
又在中,,因为为线段上一个动点(异于两端点),
所以.
故C正确.
对D,因为,为的中点,所以点的轨迹是圆弧.
故D正确.
故选:B.
例15.(2023·江西赣州·高二南康中学校考阶段练习)在等腰直角中,,,为中点,为中点,为边上一个动点,沿翻折使,点在平面上的投影为点,当点在上运动时,以下说法错误的是
A.线段为定长B.
C.线段的长D.点的轨迹是圆弧
【答案】B
【解析】如图所示,
对于A中,在为直角三角形,ON为斜边AC上的中线,为定长,即A正确;
对于C中,点D在M时,此时点O与M点重合,此时,,此时,即正确;
对于D,由A可知,根据圆的定义可知,点O的轨迹是圆弧,即D正确;
故选B.
变式29.(2023·全国·高三专题练习)如图,已知水平地面上有一半径为4的球,球心为,在平行光线的照射下,其投影的边缘轨迹为椭圆O.如图,椭圆中心为O,球与地面的接触点为E,.若光线与地面所成角为,椭圆的离心率.
【答案】/
【解析】连接,
因为,
所以,
所以,
在照射过程中,椭圆的短半轴长是球的半径,即,
如图,椭圆的长轴长是,过点向作垂线,垂足为,
由题意得,
因为,所以,
所以,得,
所以椭圆的离心率为,
故答案为:
变式30.(2023·浙江嘉兴·高三嘉兴一中校考期中)如图,在中,,,.过的中点的动直线与线段交于点.将沿直线向上翻折至,使得点在平面内的投影落在线段上.则点的轨迹长度为 .
【答案】
【解析】
因为翻折前后长度不变,所以点可以在空间中看做以为球心,AC为直径的球面上,又因为的投影始终在上,所以点所在的面垂直于底面,
故点轨迹为垂直于底面ABC的竖直面去截球所得圆面的圆弧,这个圆弧的直径为时,的长度(由余弦定理可得,所以此时),
如图,以底面点B为空间原点建系,根据底面几何关系,
得点,点,
设点,翻折后点的投影在轴上,
所以点纵坐标为0,即由,,
根据空间两点之间距离公式可得轨迹:,
又因为动点要符合空间面翻折结论:,
即,其中,
又动点N在线段AB上动,设,
故,
且,由,可计算得横坐标范围为,
且点在上方,由,计算可得圆弧所在扇形圆心角为,
所以弧长为.
故答案为:.
变式31.(2023·北京·高三专题练习)如图,在矩形中,,,为线段上一动点,现将沿折起得到,当二面角的平面角为,点在平面上的投影为,当从运动到,则点所形成轨迹的长度为 .
【答案】
【解析】根据折叠关系找出与有关的几何关系,得出点的轨迹为圆的一部分,再考虑在运动过程中扫过的弧长即可求解.
在折叠后的图中,作垂足为,连接,根据三垂线定理,,
所以就是二面角的平面角为,,
根据折叠关系,与全等,对应边上的高位置相同,即在线段上,
且是线段的中点,取的中点,连接,则,
所以点的轨迹为以为直径的圆的一部分,当从运动到,点在圆周上从点运动到
,这段弧所对圆心角为,这段弧长为.
故答案为:
题型六:翻折与动点求轨迹
例16.(2023·全国·高三专题练习)在矩形中,是的中点,,将沿折起得到,设的中点为,若将绕旋转,则在此过程中动点形成的轨迹长度为 .
【答案】/
【解析】
如图,设的中点为,绕旋转,此时平面平面,取中点,中点,中点,
连接.
,,和是等腰直角三角形,
且在旋转过程中保持形状大小不变,故动点的轨迹是以为圆心,为半径的一段圆弧,又面,
面,面,同理面,又,面面,又平面平面,
故面面,又面面,,故面,又面,,
故动点形成的轨迹长度为.
故答案为:.
例17.(2023·全国·高三专题练习)矩形ABCD中,,E为AB中点,将△ADE沿DE折起至△A'DE,记二面角A'-DE-C=θ,当θ在范围内变化时,点A'的轨迹长度为
【答案】;
【解析】取的中点为,连接,则,
故在以球心,为半径的球面上.
过作,垂足为,连接,则.
在矩形中,,故,
故,而,故平面,
故在过且垂直于的平面上,所以在以为圆心,为半径的圆上,
而为二面角的平面角,故,
故点的轨迹长度为,
故答案为:.
例18.(2023·全国·高三专题练习)如图所示,在平行四边形中,为中点,,,.沿着将折起,使到达点的位置,且平面平面.若点为内的动点,且满足,则点的轨迹的长度为 .
【答案】
【解析】因平面平面,平面平面,,于是得平面,而,则平面,
从而得PE,PD分别是PB,PD在平面内的射影,如图,,
,而,则,
在所在平面内以点E为原点,射线ED、分别为x,y轴非负半轴建立平面直角坐标系,如图,
则,设,于是得,整理得,
从而得点P的轨迹是以为圆心,4为半径的圆,圆M交分别于Q,N,
显然,圆M在内的部分是圆心角所对的弧,弧长为,
所以点的轨迹的长度为.
故答案为:
变式32.(2023·全国·高三专题练习)已知菱形ABCD的边长为2,.将菱形沿对角线AC折叠成大小为60°的二面角.设E为的中点,F为三棱锥表面上动点,且总满足,则点F轨迹的长度为 .
【答案】
【解析】连接AC、BD,交于点O,连接OB′,
ABCD为菱形,∠ABC=60°,所以AC⊥BD,OB′⊥AC,△ABC、△ACD、△AB′C均为正三角形,
所以∠B′OD为二面角B'﹣AC﹣D的平面角,于是∠B′OD=60°,
又因为OB′=OD,所以△B′OD为正三角形,所以B′D=OB′=OD=,
取OC中点P,取CD中点Q,连接EP、EQ、PQ,所以PQ∥OD、EP∥OB′,
所以AC⊥EP、AC⊥PQ,所以AC⊥平面EPQ,
所以在三棱锥B'﹣ACD表面上,满足AC⊥EF的点F轨迹的△EPQ,
因为EP=OB′,PQ=OD,EQ=B′Q,所以△EPQ的周长为,
所以点F轨迹的长度为.
故答案为:
变式33.(2023·江苏连云港·高二校考阶段练习)在矩形ABCD中,,,点E在CD上,现将沿AE折起,使面面ABC,当E从D运动到C,求点D在面ABC上的射影K的轨迹长度为( )
A.B.C.D.
【答案】D
【解析】
由题意,将沿折起,使平面平面,在平面内过点作垂足为在平面上的射影,连接,由翻折的特征知,
则,故点的轨迹是以为直径的圆上一段弧,根据长方形知圆半径是,
如图当与重合时,,所以,
取为的中点,得到是正三角形.
故,
其所对的弧长为;
故选:D.
变式34.(2023·全国·高三专题练习)已知菱形的各边长为.如图所示,将沿折起,使得点到达点的位置,连接,得到三棱锥,此时.是线段的中点,点在三棱锥的外接球上运动,且始终保持,则点的轨迹的周长为( )
A.B.C.D.
【答案】C
【解析】取中点,则,
∴平面,,又,∴,作,设点轨迹所在平面为,则平面经过点且,设三棱锥外接球的球心为的中心分别为,易知平面平面,且四点共面,由题可得,,解Rt,得,又,则三棱锥外接球半径,易知到平面的距离,
故平面截外接球所得截面圆的半径为,
∴截面圆的周长为,即点轨迹的周长为.
故选:C
变式35.(2023·全国·高三专题练习)已知△ABC的边长都为2,在边AB上任取一点D,沿CD将△BCD折起,使平面BCD⊥平面ACD.在平面BCD内过点B作BP⊥平面ACD,垂足为P,那么随着点D的变化,点P的轨迹长度为( )
A.B.C.D.π
【答案】C
【解析】由题意,在平面BCD内作BQ⊥CD,交CD于Q,因为平面BCD⊥平面ACD,平面BCD与平面ACD交于CD,所以BQ⊥平面ACD,又BP⊥平面ACD,所以P,Q两点重合,于是随着点D的变化,BP⊥CD始终成立,可得在平面ABC中,BP⊥CP始终成立,即得点P的轨迹是以BC为直径的圆的一部分,由题意知随着点D的变化,∠BCD的范围为,可得点P的轨迹是以BC为直径(半径为1)的圆的,即得点P的轨迹长度为.
故选:C.
变式36.(2023·广东中山·高三华南师范大学中山附属中学校考期中)如图,在长方形中,,,点为线段上一动点,现将沿折起,使点在面内的射影在直线上,当点从运动到,则点所形成轨迹的长度为
A.B.C.D.
【答案】C
【解析】由题意,将△AED沿AE折起,使平面AED⊥平面ABC,在平面AED内过点D作DK⊥AE,K为垂足,由翻折的特征知,连接D'K,
则D'KA=90°,故K点的轨迹是以AD'为直径的圆上一弧,根据长方形知圆半径是,
如图当E与C重合时,
AK==,
取O为AD′的中点,得到△OAK是正三角形.
故∠KOA=,∴∠KOD'=,
其所对的弧长为=,
故选:
变式37.(2023·全国·高三专题练习)如图,在等腰梯形中,,分别是底边的中点,把四边形沿直线折起使得平面平面.若动点平面,设与平面所成的角分别为(均不为0).若,则动点的轨迹围成的图形的面积为( )
A.B.C.D.
【答案】D
【解析】连接,∵平面⊥平面,交线为,BE,CF在平面BCFE中,且BE,CF都垂直于交线EF,由面面垂直的性质定理得BE⊥平面ADFE,CF⊥平面ADFE,∴∠BPE,∠CPF分别为直线PB,PC与平面ADFE所成的角,∠BPE=,∠CPF=.
∵PE,PF⊂平面ADFE,∴BE⊥PE,CF⊥PF,
∴,,
∵,,∴.
以EF所在直线为x轴,EF的垂直平分线为y轴建立坐标系,如图所示:
设,,,则
∴3x2+3y2+5ax+a2=0,即,轨迹为圆,面积为.
故答案选:.
【讲通练透】重难点突破03 立体几何中的截面问题(八大题型)-2024年高考数学重难点突破精讲: 这是一份【讲通练透】重难点突破03 立体几何中的截面问题(八大题型)-2024年高考数学重难点突破精讲,文件包含重难点突破03立体几何中的截面问题八大题型原卷版docx、重难点突破03立体几何中的截面问题八大题型解析版docx等2份试卷配套教学资源,其中试卷共76页, 欢迎下载使用。
【讲通练透】重难点突破02 向量中的隐圆问题(四大题型)-2024年高考数学重难点突破精讲: 这是一份【讲通练透】重难点突破02 向量中的隐圆问题(四大题型)-2024年高考数学重难点突破精讲,文件包含重难点突破02向量中的隐圆问题四大题型原卷版docx、重难点突破02向量中的隐圆问题四大题型解析版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
【讲通练透】重难点突破02 解三角形图形类问题(十大题型)-2024年高考数学重难点突破精讲: 这是一份【讲通练透】重难点突破02 解三角形图形类问题(十大题型)-2024年高考数学重难点突破精讲,文件包含重难点突破02解三角形图形类问题十大题型原卷版docx、重难点突破02解三角形图形类问题十大题型解析版docx等2份试卷配套教学资源,其中试卷共75页, 欢迎下载使用。












