【讲通练透】专题06 立体几何（解答题）（文）-2021-2023年高考真题分享汇编（全国通用）

这是一份【讲通练透】专题06 立体几何（解答题）（文）-2021-2023年高考真题分享汇编（全国通用），文件包含专题06立体几何解答题文全国通用原卷版docx、专题06立体几何解答题文全国通用解析版docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
一、高考真题汇编的意义
1、增强高考考生的复习动力和信心。
2、提高高考考生的复习效率。使考生能够更好地梳理复习的重点，提高复习效率。
3、加深考生对知识点的理解和掌握。
二、高考真题汇编的内容
1、高考试题收录。高考真题汇编收录高考真题，涵盖了高考考试的各个学科。
2、答案解析。高考真题汇编提供了详细的答案解析，加深考生对知识点的理解和掌握。
3、复习指导。高考真题汇编还提供了一些复习指导，提高复习效率。
三、高考真题汇编的重要性
高考真题汇编不仅可以提高考生的复习动力和信心，增强考生的复习效率，而且还可以加深考生对知识点的理解和掌握，使考生更好地把握考试方向，为高考复习提供了有力的支持。本文介绍了高考真题汇编的意义、内容和重要性，分析了它对高考考生的重要作用，强调了它在高考复习中的重要性。
专题06 立体几何（解答题）（文）
知识点目录
知识点1：线面角
知识点2：直接法求体积问题
知识点3：换底法求体积问题
知识点4：割补法求体积问题
知识点5：距离及几何体的高问题
近三年高考真题
知识点1：线面角
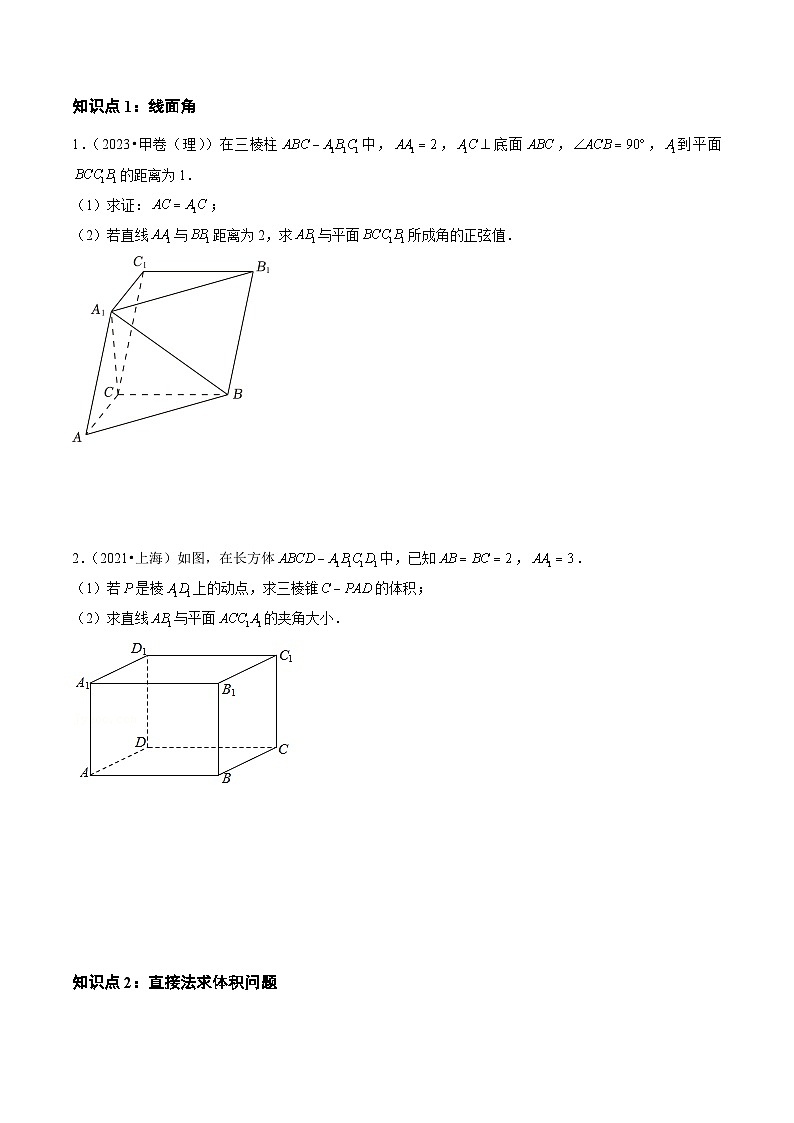
1．（2023•甲卷（理））在三棱柱中，，底面，，到平面的距离为1．
（1）求证：；
（2）若直线与距离为2，求与平面所成角的正弦值．
【解析】（1）证明：取的中点，连接，
底面，底面，
，，，
底面，底面，
，，，
，平面，
平面，平面平面，
到平面的距离为1，
到的距离为1，
，
；
（2）过作交的延长线与，连接，
取的中点，连接，
四边形为平行四边形，
平面，
，平面，
平面，
，
，
为直线与距离，
，，
由（1）可知平面，
为与平面所成角的角，
易求得，
，
，，
．
与平面所成角的正弦值为．
【点评】本题考查线线相等的证明，考查线面角的求法，属中档题．
2．（2021•上海）如图，在长方体中，已知，．
（1）若是棱上的动点，求三棱锥的体积；
（2）求直线与平面的夹角大小．
【解析】（1）如图，在长方体中，；
（2）连接，
，
四边形为正方形，则，
又，，
平面，
直线与平面所成的角为，
．
直线与平面所成的角为．
【点评】本题考查三棱锥体积的求法，考查线面角的求解，考查推理能力及运算能力，属于中档题．
知识点2：直接法求体积问题
3．（2023•乙卷（文））如图，在三棱锥中，，，，，，，的中点分别为，，，点在上，．
（1）求证：平面；
（2）若，求三棱锥的体积．
【解析】 （1）证明：在中，作，垂足为，设，则，
因为，所以，所以，即，解得，
又因为，所以，且，
所以，所以，即，解得，
即，所以是的中点，是的中点，
又因为是的中点，所以，同理，，所以，
又因为平面，平面，
所以平面；
（2）过作垂直的延长线交于点，因为，是中点，所以，在中，，，所以，
因为，，所以，又，，平面，所以平面，
又平面，所以，
又，，平面，
所以平面，即三棱锥的高为，
因为，所以，
所以，
的面积为，
所以三棱锥的体积为．
【点评】本题考查了直线与平面平行的应用问题，也考查了几何体体积计算问题，是中档题．
4．（2022•乙卷（文））如图，四面体中，，，，为的中点．
（1）证明：平面平面；
（2）设，，点在上，当的面积最小时，求三棱锥的体积．
【解析】证明：（1），，，
，
，又为的中点．
，
，为的中点．
，又，
平面，
又平面，
平面平面；
（2）由（1）可知，
，，是等边三角形，边长为2，
，，，，
，，
又，，
平面，
由（1）知，，连接，则，
，
当时，最短，此时的面积最小，
过点作于点，则，平面，
，
，，
三棱锥的体积．
【点评】本题主要考查了面面垂直的判定定理，考查了三棱锥的体积公式，同时考查了学生的空间想象能力与计算能力，是中档题．
5．（2021•甲卷（文））已知直三棱柱中，侧面为正方形，，，分别为和的中点，．
（1）求三棱锥的体积；
（2）已知为棱上的点，证明：．
【解析】（1）在直三棱柱中，，
又，，，平面，
平面，
，
平面，
，
又，故，
，
而侧面为正方形，
，
，即三棱锥的体积为；
（2）证明：如图，取中点，连接，，设，
点是的中点，点时的中点，
，
，
、、、四点共面，
由（1）可得平面，
平面，
，
，且这两个角都是锐角，
，
，
，
又，，平面，
平面，
又平面，
．
【点评】本题主要考查三棱锥体积的求法以及线线，线面间的垂直关系，考查运算求解能力及逻辑推理能力，属于中档题．
6．（2021•乙卷（文））如图，四棱锥的底面是矩形，底面，为的中点，且．
（1）证明：平面平面；
（2）若，求四棱锥的体积．
【解析】（1）证明：底面，平面，
，
又，
，，平面．
平面．
平面，
平面平面；
（2）由底面，
即为四棱锥的高，是直角三角形；
底面是矩形，，为的中点，且．
设，取的中点为．作交于，
连接，，，
可得，，
那么．且．，，
．
是直角三角形，
根据勾股定理：，则；
由是直角三角形，
可得，
解得．
底面的面积，
则四棱锥的体积．
【点评】本题考查平面与平面垂直的判定，考查空间想象能力与思维能力，体积计算，考查运算求解能力，是中档题．
7．（2021•上海）四棱锥，底面为正方形，边长为4，为中点，平面．
（1）若为等边三角形，求四棱锥的体积；
（2）若的中点为，与平面所成角为，求与所成角的大小．
【解析】（1）为等边三角形，且为中点，，
，
又平面，
四棱锥的体积．
（2）平面，
为与平面所成角为，即，
为等腰直角三角形，
，分别为，的中点，
，
，
，
或其补角即为与所成角，
平面，，
又，，、平面，
平面，，
在中，，
故与所成角的大小为．
【点评】本题考查棱锥的体积、线面角和异面直线夹角的求法，理解线面角的定义，以及利用平移法找到异面直线所成角是解题的关键，考查学生的空间立体感、逻辑推理能力和运算能力，属于基础题．
知识点3：换底法求体积问题
8．（2021•新高考Ⅰ）如图，在三棱锥中，平面平面，，为的中点．
（1）证明：；
（2）若是边长为1的等边三角形，点在棱上，，且二面角的大小为，求三棱锥的体积．
【解析】（1）证明：因为，为的中点，所以，
又平面平面，平面平面，平面，
所以平面，又平面，
所以；
（2）过作，交于点，过作于点，连结，
由题意可知，，又平面
所以平面，又平面，
所以，又，
所以平面，又平面，
所以，
则为二面角的平面角，即，
又，
所以，则，
故，
所以，
因为，
则，
所以，则，
所以，则，
所以．
知识点4：割补法求体积问题
9．（2022•甲卷（文））小明同学参加综合实践活动，设计了一个封闭的包装盒．包装盒如图所示：底面是边长为8（单位：的正方形，，，，均为正三角形，且它们所在的平面都与平面垂直．
（1）证明：平面；
（2）求该包装盒的容积（不计包装盒材料的厚度）．
【解析】（1）证明：如图所示，将几何体补形为长方体，
做于点，做于点，
由于底面为正方形，，均为等边三角形，
故等边三角形的高相等，即，
由面面垂直的性质可知，均与底面垂直，
则，四边形为平行四边形，则，
由于不在平面内，在平面内，
由线面平行的判断定理可得平面．
（2）易知包装盒的容积为长方体的体积减去四个三棱锥的体积，
其中长方体的高，
长方体的体积，
一个三棱锥的体积，
则包装盒的容积为．
【点评】本题主要考查线面平行的判定，空间几何体体积的计算等知识，属于中等题．
知识点5：距离及几何体的高问题
10．（2023•甲卷（文））如图，在三棱柱中，平面，．
（1）证明：平面平面；
（2）设，，求四棱锥的高．
【解析】（1）底面，面，
，又，，平面，，
平面，又平面，
平面平面；
（2）平面，，平面，
，，
，，
△，
，
底面，面，
，，
，，
，
过作于，，
为的中点，，
由（1）可知平面，
四棱锥的高为1．
【点评】本题考查面面垂直的证明，考查四棱锥的高的求法，属中档题．
11．（2023•上海）已知三棱锥中，平面，，，，为中点，过点分别作平行于平面的直线交、于点，．
（1）求直线与平面所成角的大小；
（2）求直线到平面的距离．
【解析】（1）连接，，
平面，
为直线与平面所成的角，
在中，，，
为中点，，
，即直线与平面所成角为；
（2）由平面，平面，，
平面平面，平面，平面，
平面，平面，
，，，，平面，
平面，为直线到平面的距离，
平面，平面，平面平面，
，为中点，为中点，，
直线到平面的距离为2．
【点评】本题考查直线与平面所成的角，考查直线与平面的距离的求法，属中档题．