苏科版九年级下册7.2 正弦、余弦说课ppt课件

这是一份苏科版九年级下册7.2 正弦、余弦说课ppt课件，共36页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，余弦的概念，锐角三角函数等内容，欢迎下载使用。

正弦、余弦的概念锐角三角函数锐角三角函数之间的关系利用计算器计算锐角的正弦值或余弦值
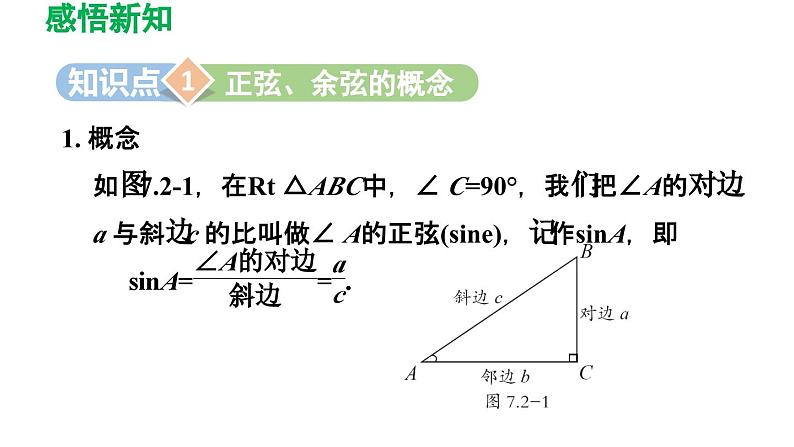
1. 概念如图7.2-1，在Rt △ABC中，∠ C=90°，我们把∠A的对边a 与斜边c 的比叫做∠ A的正弦(sine)，记作sinA，即
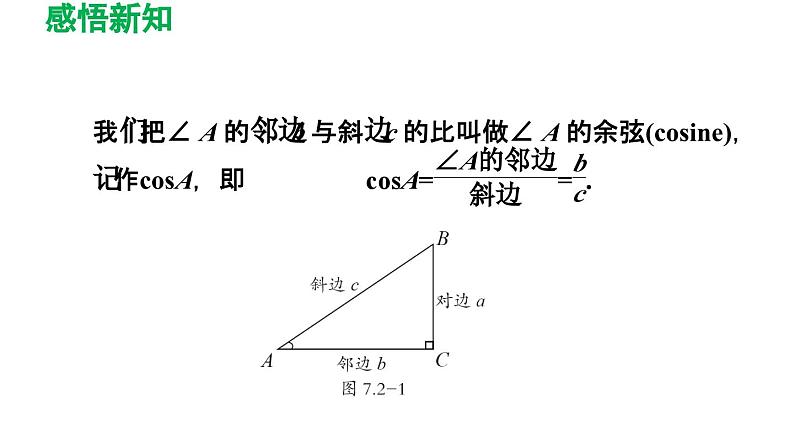
我们把∠ A 的邻边b 与斜边c 的比叫做∠ A 的余弦(csine)，记作csA，即
特别警示 ：①正弦、余弦与正切类似，都是一个比值，是没有单位的数值，它们只与锐角的大小有关，而与三角形的边的长短无关.②正弦、余弦与正切类似，符号后面可以直接写锐角的度数，如sin28°，cs8°等.
2. 表示法(1)在sin A，cs A 中，表示正弦、余弦的符号一定要小写，不能大写.(2)当锐角是用一个大写英文字母或一个小写希腊字母表示时，它的正弦、余弦习惯上省略角的符号，如sin A，cs α 等；当锐角是用三个大写英文字母或数字表示时，它的正弦、余弦不能省略角的符号，如sin ∠ ABC，cs ∠ 1 等.
(3)“sin A”“cs A”“tan A” 是整体符号， 不能理解为“sin·A”“cs ·A”“tan·A”.(4)sin2A表示sin A·sin A=(sin A)2，不能写成sin A2；cs2A 表示cs A·cs A=(cs A)2，不能写成cs A2；tan2A表示tan A·tan A=(tan A)2，不能写成tan A2.
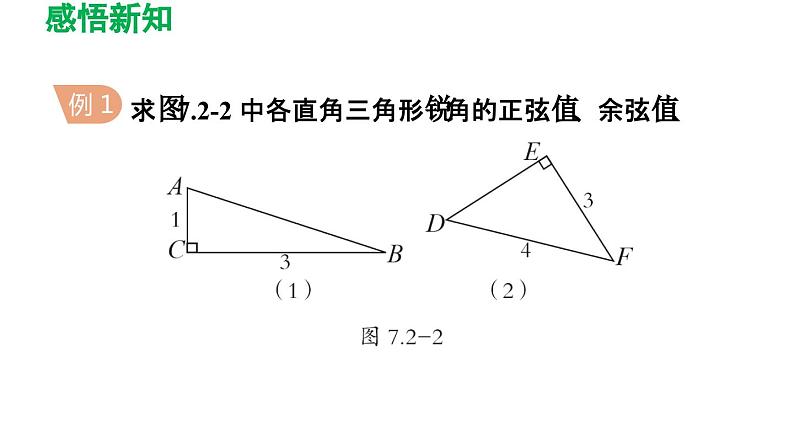
求图7.2-2 中各直角三角形锐角的正弦值、余弦值.
解题秘方：首先利用勾股定理得出AB 以及DE 的长，进而利用正弦、余弦的概念得出答案.
思路点拨：根据勾股定理，可得第一个直角三角形的斜边长，第二个直角三角形的直角边长，再根据正弦、余弦的概念即可得到答案.
在Rt △ABC 中，∠ C=90°若AB=4，sinA= ，则斜边AB上的高CD的长为_______ .
解题秘方：如图7.2-3，在Rt △ ABC 中，利用正弦定义可计算出BC= ，再利用勾股定理计算出AC= ，然后利用面积法计算CD 的长.
解题通法：已知正弦值或余弦值求线段的长的基本思路是根据正弦或余弦的定义列方程求解.
1. 概念 在Rt △ ABC 中， 的值都随∠ A 的大小变化而变化，都随∠ A 的大小确定而唯一确定，∠ A 的正弦、余弦和正切都是∠ A 的三角函数.
2. 锐角三角函数值的变化规律(1)因为Rt △ABC的三边长都是正数，所以锐角的三角函数值也都是正数；又因为直角三角形的斜边长大于任意一条直角边长，所以有tan A>0,0特别提醒：sin x ，cs x和tan x都是以x为自变量的函数，一旦x 的度数确定，它们的值就唯一确定，即锐角三角函数值随角度的变化而变化 .
如图7.2-4，在等腰三角形ABC 中，AB=AC，如果2AB=3BC，求∠ B 的三个三角函数值.
解题秘方：紧扣“锐角三角函数的定义的前提是在直角三角形中”这一特征，用“构造直角三角形法”求解.
特别提醒：求锐角三角函数值的方法：锐角三角函数是在直角三角形的条件下定义的，因此当题目要求某一个锐角的三角函数值时，先观察所要求的角是否在题目中没有直角三角形时，就需要我们作辅助线构造与该角有关的直角三角形.
解：过点A 作AD ⊥ BC 于点D，如图7.2-4，∵ AB=AC，∴ BD=DC.又∵ 2AB=3BC，∴ .设AB=AC=3k(k>0)，则BC=2k. ∴ BD=CD=k，
比较大小：(1)cs35°___cs45°，tan50°___tan60°；
解题秘方：紧扣锐角的三角函数值变化规律即可求解.
解：因为35°＜ 45°，根据余弦值随角度的增大而减小，可知cs35°＞ cs45°；因为50°＜ 60°，根据正切值随角度的增大而增大，可知tan50°＜ tan60° .
(2)若sinα ＝ 0.3276，sinβ ＝ 0.3274，则α_____β．
解：因为sinα ＝ 0.3276，sinβ ＝ 0.3274，0.3276 ＞ 0.3274，根据正弦值随角度的增大而增大，可知α ＞ β．
解题通法：比较锐角的三角函数值大小的一般策略：①正弦(或正切)之间比较大小，角度增大，正弦值(或正切值)也增大，反之也成立；②余弦之间比较大小，角度增大，余弦值反而减小，反之也成立．
锐角三角函数之间的关系
1. 同一锐角的三角函数之间的关系(1)平方关系：sin2A+cs2A=1.(2)商除关系： =tanA.2. 互余两角的三角函数之间的关系sinA=cs(90°－∠ A).csA=sin(90°－∠ A).tanA•tan(90°－∠ A)=1.
深度理解：①锐角三角函数之间的关系都可用定义推理得出.②锐角三角函数定义速记口诀：正弦等于对比斜，余弦等于邻比斜，正切等于对比邻，函数特点要牢记.
已知α 为锐角且sinα = ，求cs α ，tanα 的值.
解题秘方：紧扣“同一锐角三角函数间的关系”求解.
特别警示：利用同角三角函数间的关系求三角函数值时，需注意各个锐角三角函数值的范围：即00，对于不在其范围内的函数值，应舍去.
利用计算器计算锐角的正弦值或余弦值
1. 求以度为单位的锐角正弦值的一般步骤利用计算器可求锐角的正弦值，先依次按计算器上的 键，再依次按数字键、 键即可.2. 求以度、分、秒为单位的正弦值的一般步骤求以度、分、秒为单位的锐角的正弦值时，在计算器的面板上先按 键,再按度的数字键，再按 键，按分的数字键，再按 键, 按秒的数字键，再按 键，最后按 键.
特别提醒：①利用计算器计算锐角的余弦值的步骤与求正弦值的步骤大致相同；②不同的计算器操作程序不同，按键规定一般也不一样.
［动手操作题］利用计算器求下列正弦值或余弦值(精确到0.01).(1)sin 72°； (2)cs 11° 22′ 30″．
解：(1)sin 72°≈ 0.95.(2)cs 11°22′30″≈ 0.98．
解题秘方：紧扣计算器的说明方法，按照步骤进行操作．
特别提醒：①注意不同类型计算器的按键顺序；②注意精确的数位要求.