初中数学苏科版九年级下册7.6 用锐角三角函数解决问题教案配套ppt课件

这是一份初中数学苏科版九年级下册7.6 用锐角三角函数解决问题教案配套ppt课件，共38页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，坡度的应用，有关仰角和俯角的应用，方向角的应用等内容，欢迎下载使用。

解坡角、坡度的应用有关摩天轮旋转高度的应用有关仰角和俯角的应用方向角的应用
1. 坡角与坡度(坡比)的定义(1)坡角：坡面与水平面所成的夹角，如图7.6-1 中的α.(2)坡度(坡比)：我们通常把坡面的垂直高度h 和水平宽度l 的比叫做坡度(坡比)(如图7.6-1 所示)，坡度(坡比)也可写成i = h ∶ l 的形式，在实际应用中常表示成1 ∶ x 的形式.
特别提醒:① 坡度是两条线段的比值，不是度数.②表示坡度时，通常把比的前项取作1，后项可以是小数.③物体的倾斜程度通常可用物体的坡度表示，坡度越大，坡角越大，坡面越陡；反之，坡度越小，坡角越小，坡面越缓.
2. 坡度与坡角的关系i= =tanα，即坡度是坡角的正切值，坡角越大，坡度也就越大.
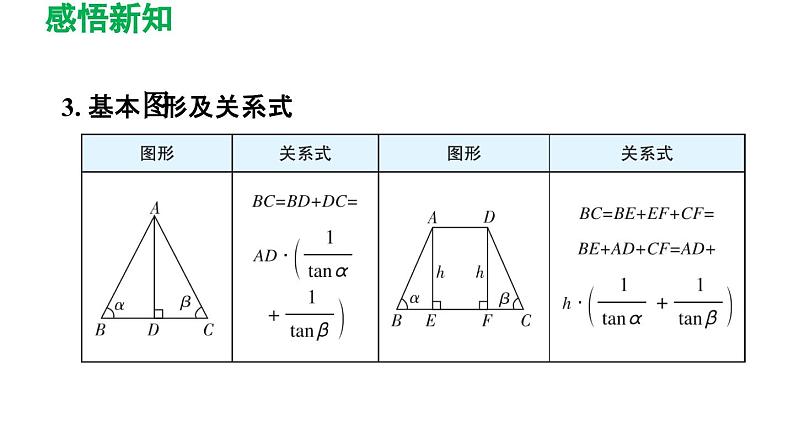
3. 基本图形及关系式
4. 解决实际问题的一般步骤(1)画出平面图形，将实际问题抽象为数学问题，转化为解直角三角形的问题；(2)根据已知条件的特点，灵活选用锐角三角函数等知识解直角三角形；(3)得到数学问题的答案；(4)得到实际问题的答案.
特别提醒:当实际问题中涉及的图形可以直接转化为直角三角形时，可利用解直角三角形的知识直接求解.
某工程队承包了一段铁路的施工，该铁路要经过某一隧道，如图7.6-2，已知隧道口分别为D，E，为了如期完工，需测量出DE 的长度，为此，该工程队在山的一侧选取适当的点C，测得BC=200 m，∠ ABC=105°，∠ C=45°，AD=18 m，BE=32 m，且A，D，E，B在同一条直线上，已知该工程限定时间为10 天，该工程队平均每天至少需要施工多少米？
解题秘方：在建立的非直角三角形模型中，用“化斜为直法”解含公共直角边的直角三角形.
教你一招：解直角三角形的实际应用问题的求解方法：①根据题目中的已知条件，将实际问题抽象为解直角三角形的数学问题，画出平面几何图形，弄清已知条件中各量之间的关系；②若条件中有直角三角形，则直接选择合适的三角函数关系求解即可；若条件中没有直角三角形，一般需添加辅助线构造直角三角形，再选用合适的三角函数关系求解.
解：如图7.6-2，过点B 作BF ⊥ AC 于点F，∵∠ABC=105°，∠ C=45°，∴∠A=30°.在Rt △BFC中，∵ sin C= ，∴ BF=BC·sin C=200× =100 (m).在Rt △ AFB 中，∵∠ A=30°，∴ AB=2BF=200 m.又∵ AD=18 m，BE=3 m，∴ DE=AB－AD－BE=200 －18 －32 =150 2 (m).∵ 150 ÷10=15 (m)，∴该工程队平均每天至少需要施工15 m.
有关摩天轮旋转高度的应用
随着摩天轮的旋转，游客相对于地面的高度也发生着变化.如图7.6-3 所示，点C 距离地面的高度CH ＝ DA ＝ OA－OD＝ OB＋AB－OD＝ OB ＋AB －OC•cs ∠COD＝ R＋AB － R•cs ∠COD.
特别提醒：类似问题很多，如荡秋千问题、跷跷板问题、大风车问题等.
如图7.6-4，是一个匀速旋转(指每分钟旋转的弧长或圆心角相同)的摩天轮的示意图，O 为圆心，AB 为水平地面，假设摩天轮的直径为80 米，最低点C离地面的高度为6 米，旋转一周所用的时间为6 分钟，小明从点C 乘坐摩天轮，请问：
解题秘方：紧扣“构造法”构造直角三角形求解.
解法提醒:(1)设小明从点C乘坐摩天轮，经过2 分钟后到达点E，延长CO与⊙O交于点F，过点E作EG⊥OF于点G，如图7.6-4.根据旋转一周所用的时间为6分钟，小明从点C乘坐摩天轮经过2分钟，可知∠COE=120°，根据平角的定义可知∠GOE=60°，根据三角函数可求出OG的长，进而求出小明离开地面的高度；(2)根据圆的面积公式可求.
解：设小明从点C 乘坐摩天轮，经过2 分钟后到达点E，延长CO 与⊙ O 交于点F，过点E 作EG ⊥ OF 于点G，如图7.6-4，根据旋转一周所用的时间为6 分钟，小明从点C 乘坐摩天轮经过2 分钟，可知∠ COE=120°，∴∠ GOE=60° .在Rt △ EOG 中，OG=OE×cs ∠ GOE= ×80×cs60° =20(米).∴ DG=CD+CO+OG=6+ ×80+20=66(米).答：小明离开地面的高度是66 米.
(1)经过2 分钟后，小明离开地面的高度是多少米？
解：∵ 80+6=86(米)，86 米=0.086 千米，∴ π ≈ 28(平方千米).答：他看到的地面景物大约有28 平方千米.
(2)若小明到了最高点，在视线没有阻挡的情况下能看到周围3千米远的景物，则他看到的地面景物有多大面积？(精确到1 平方千米)
1. 仰角和俯角的定义在视线与水平线所成的角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角.
2. 示图(如图7.6-5)
特别提醒:●仰角和俯角是视线相对于水平线而言的，不同位置的仰角和俯角是不同的，可巧记为“上仰下俯”.●实际问题中遇到仰角或俯角时，要放在直角三角形中或转化到直角三角形中，注意确定水平线.
问题中有两个或两个以上的直角三角形，当其中一个直角三角形不能求解时，可考虑分别由两个直角三角形找出含有相同未知元素的关系式，运用方程求解.
如图7.6-6，在数学活动课中，小敏为了测量校园内旗杆CD 的高度，先在教学楼的底端A 处，观测到旗杆顶端C 的仰角∠ CAD=60°，然后爬到教学楼上的B 处，观测到旗杆底端D 的俯角是30°，已知AB 高4 米.
解题秘方：将实际问题转化为解直角三角形问题求解.
方法点拨：求解有关仰角与俯角的问题，关键是根据仰角、俯角的定义画出水平线，找准视角，建立数学模型后构造直角三角形，并结合图形利用锐角三角函数解直角三角形.
解：∵ 在教学楼上的B 处观测旗杆底端D的俯角是30 °，∴∠ ADB=30° .在Rt △ ABD 中，∵∠BAD=90°，∠ADB=30°，AB=4 米，因此，教学楼与旗杆的水平距离AD 是4 米.
(1)求教学楼与旗杆的水平距离AD；(结果保留根号)
解：在Rt △ ACD 中，∵∠ ADC=90°，∠ CAD=60°，AD=4 米，∴ CD=AD·tan60° =4 × =12(米).因此，旗杆CD 的高度是12 米.
(2)求旗杆CD的高度.
1. 方向角的定义指北或指南的方向线与目标方向线所成的小于90°的角叫做方向角.特别警示：方向角和方位角不同，方位角是指从某点的指北方向线起，按顺时针方向到目标方向线之间的水平夹角，变化范围为0°~360°，而方向角的变化范围是0°~ 90°
2. 示图如图7.6-7 所示，目标方向线OA，OB，OC 的方向角分别可以表示为北偏东30°、南偏东45°、北偏西30°，其中南偏东45°习惯上又叫做东南方向，北偏东45°习惯上又叫做东北方向，北偏西45°习惯上又叫做西北方向，南偏西45°习惯上又叫做西南方向.
特别提醒：①因为方向角是指北或指南方向线与目标方向线所成的角，所以方向角通常都写成“北偏……” “南偏……”的形式.②解决实际问题时，可利用正南、正北、正西、正东方向线构造直角三角形来求解.③观测点不同，所得的方向角也不同，但各个观测点的南北方向线是互相平行的，通常借助于此性质进行角度转换.
为了维护海洋权益，新组建的国家海洋局加大了在南海的巡逻力度，一天，我国两艘海监船刚好在我国某岛东西海岸线上的A，B两处巡逻，同时发现一艘不明国籍的船只停在C 处海域，如图7.6-8 所示，AB=60 海里，在B 处测得C 在北偏东45°的方向上，在A 处测得C 在北偏西30°的方向上，在海岸线AB 上有一灯塔D，测得AD=120 海里.
解题秘方：建立数学模型后，用“化斜为直”法，将斜三角形问题转化为直角三角形问题求解.
解：如图7.6-8，过点C作CE⊥AB于点E，可得∠ACE=30°，∠BCE=45°，设AE=x 海里，则在Rt △ACE中，CE= x海里，AC=2x海里，在Rt△BCE中，BE=CE= x海里，BC= x海里.∵ AB=AE+BE，∴ x+ x=60( )，解得x=60 .∴ AC=120 海里，BC=120 海里
(1)分别求出A 与C 及B 与C 的距离AC，BC；(结果保留根号)
(2)已知在灯塔D 周围100 海里范围内有暗礁群，在A 处的海监船沿AC 前往C 处盘查，途中有无触礁的危险？(参考数据： ≈ 1.41， ≈ 1.73， ≈ 2.45)
解：如图7.6-8，过点D 作DF ⊥ AC 于点F.易知∠ DAF=60° . 在Rt △ AFD 中，∵ DF=DA·sin60° = ×120( )=60(3 )≈ 106.8(海里)>100 海里，∴途中无触礁的危险.
解法提醒：求解是否触礁或是否受台风或噪声影响等问题的方法：一般都是求出暗礁中心到航线的距离，或城市中心(目标中心)到台风中心的距离，或是学校到噪声源的距离，将这些距离与暗礁半径或台风影响半径或噪声影响半径比较大小，距离小于或等于半径有危险或影响，距离大于半径没有危险或影响.
图解:通过CE将原三角形分成两个直角三角形，如图7.6-9 所示(单位：海里).
用锐角三角函数解决问题