初中数学苏科版九年级下册第5章 二次函数5.4 二次函数与一元二次方程学案设计

这是一份初中数学苏科版九年级下册第5章 二次函数5.4 二次函数与一元二次方程学案设计，共33页。学案主要包含了即学即练1，即学即练2，即学即练3，即学即练4等内容，欢迎下载使用。
目标导航
知识精讲
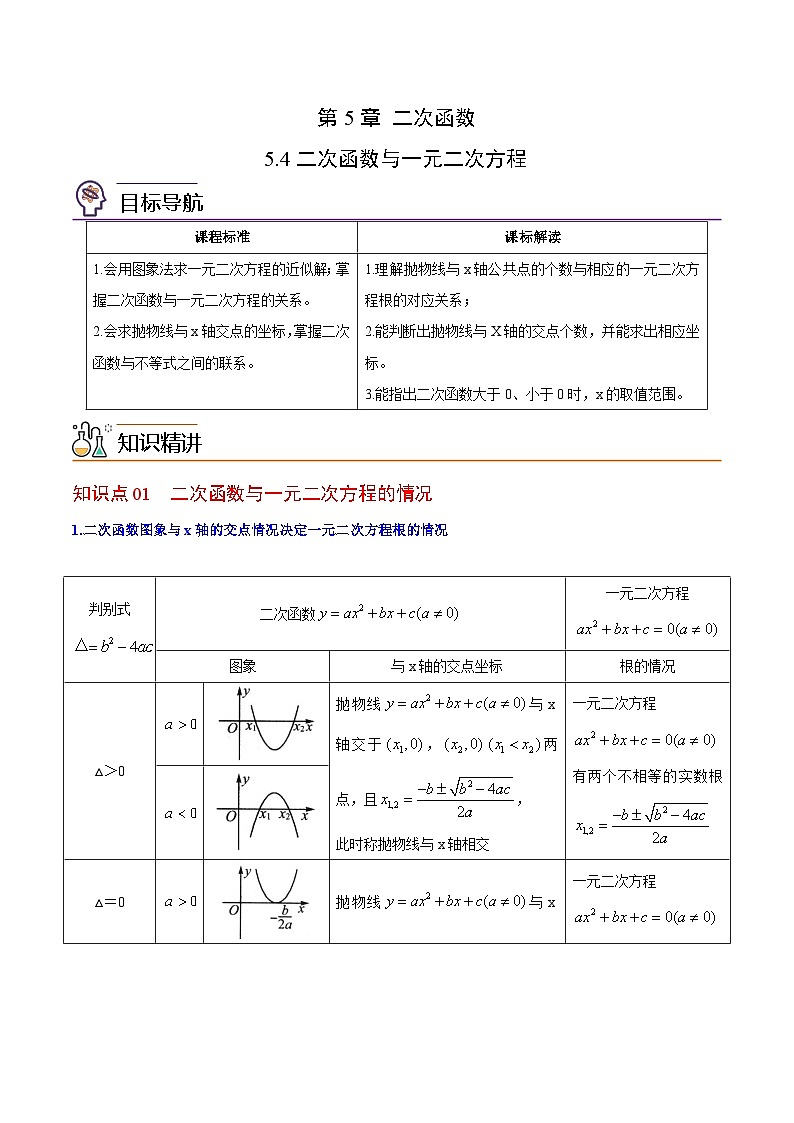
知识点01 二次函数与一元二次方程的情况
1.二次函数图象与x轴的交点情况决定一元二次方程根的情况
【微点拨】
二次函数图象与x轴的交点的个数由的值来确定的.
(1)当二次函数的图象与x轴有两个交点时，，方程有两个不相等的实根；
(2)当二次函数的图象与x轴有且只有一个交点时，，方程有两个相等的实根；
(3)当二次函数的图象与x轴没有交点时，，方程没有实根.
2.抛物线与直线的交点问题
抛物线与x轴的两个交点的问题实质就是抛物线与直线的交点问题．我们把它延伸到求抛物线(a≠0)与y轴交点和二次函数与一次函数的交点问题．
抛物线(a≠0)与y轴的交点是(0，c)．
抛物线(a≠0)与一次函数(k≠0)的交点个数由方程组的解的个数决定．
当方程组有两组不同的解时两函数图象有两个交点；
当方程组有两组相同的解时两函数图象只有一个交点；
当方程组无解时两函数图象没有交点．
总之，探究直线与抛物线的交点的问题，最终是讨论方程(组)的解的问题．
【微点拨】
求两函数图象交点的问题主要运用转化思想，即将函数的交点问题转化为求方程组解的问题或者将求方程组的解的问题转化为求抛物线与直线的交点问题．
【即学即练1】观察下列表格，估计一元二次方程的正数解在（ ）
A．－1和0之间B．0和1之间C．1和2之间D．2和3之间
【答案】C
【解析】解：令x2＋3x－5，
当时，，
当时，，
x2＋3x－5=0的一个正数x的取值范围为1＜x＜2，
故选C．
【即学即练2】如图，抛物线的对称轴是，关于x的方程的一个根为，则另一个根为（ ）
A．B．C．D．0
【答案】C
【解析】解：∵抛物线的对称轴是，
∴，即，
设的另一根为m，
利用根与系数的关系可得：，
∴．
故选：C
知识点02 抛物线与x轴的两个交点的距离公式
当△＞0时，设抛物线与x轴的两个交点为A(，0)，B(，0)，则、是一元二次方程的两个根．由根与系数的关系得，．
∴
即 （△＞0）
【即学即练3】若，是方程（c为常数）两个不相等的实数根，且满足，则c的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】解：∵，是方程（c为常数）两个不相等的实数根，
∴，解得：，
设，
∵1＞0，
∴抛物线开口向上，
∵，
∴当x=1时，y＞0，
∴，解得：，
∴c的取值范围是．
故选：C
知识点03 抛物线与不等式的关系
二次函数(a≠0)与一元二次不等式(a≠0)及(a≠0)之间的关系如下：
注：a＜0的情况请同学们自己完成．
【微点拨】
抛物线在x轴上方的部分点的纵坐标都为正，所对应的x的所有值就是不等式的解集；在x轴下方的部分点的纵坐标都为负，所对应的x的所有值就是不等式的解集．不等式中如果带有等号，其解集也相应带有等号．
【即学即练4】如图，二次函数y＝ax2+bx+c的图象与x轴的右交点A（5，0），对称轴是直线x＝2，当ax2+bx+c＞16a时，x的取值范围是( )
A．x＜﹣1或x＞5B．﹣1＜x＜5C．﹣3＜x＜7D．x＜﹣3或x＞7
【答案】C
【解析】解：∵y＝ax2+bx+c的对称轴是直线x＝2，
∴2，
∴b＝﹣4a，
∴y＝ax2﹣4ax+c，
∵与x轴右交点为(5,0)，
∴25a﹣20a+c＝0，
∴c＝﹣5a，
∴y＝ax2﹣4ax﹣5a，
∴ax2﹣4ax﹣5a＞16a，
∴ax2﹣4ax﹣21a＞0，
∵a＜0，
∴x2﹣4x﹣21＜0（两边同除以a，不等号方向改变），
y＝x2﹣4x﹣21，a＝1，开口向上，
当x2﹣4x﹣21＝0时，
（x﹣7)(x+3)＝0，
∴x1＝7，x2＝﹣3，
y＝x2﹣4x﹣21的图像如图，
∴x的取值范围是﹣3＜x＜7，
故选：C．
能力拓展
考法01 二次函数图像与坐标轴的交点问题
【典例1】 关于二次函数的三个结论，①图象与y轴的交点为；②对任意实数m，都有与对应的函数值相等；③图象经过点；其中，正确结论是（ ）
A．①②B．②③C．①③D．①②③
【答案】D
【解析】解：令x=0，可得y=-5，即二次函数与y轴的交点为（0，-5），故①正确；
此二次函数的对称轴为，根据二次函数的对称性，可得对任意实数m，都有 x1=2+m 与 x2=2−m 对应的函数值相等，故②正确；
当x=4时，y=16a-16a-5=-5，即函数的图象经过（4，-5），故③正确；
故选D．
考法02 根据二次函数的图像确定相应方程根的情况
【典例2】抛物线的对称轴为，若关于的二次方程在范围内有实数根，则的取值范围是（ ）
A．B．
C．D．
【答案】C
【解析】解：∵抛物线的对称轴为，
∴，解得：b=6，
∴，
∴二次方程在范围内有实数根看作抛物线与直线y=－t在内有交点，
当x=－1时，y=－4，
当x=4时，y=11，
当x=3时，y=12，
∴抛物线在的范围是－4＜y≤12，
∴－4＜－t≤12，则－12≤t＜4，
故选：C．
分层提分
题组A 基础过关练
1．抛物线与轴的交点坐标为（ ）
A．(-3，0)B．(0，-3)C．D．
【答案】B
【解析】解：当x=0时，y=-3，
则抛物线y=x2-3与y轴交点的坐标为（0，-3），
故选：B．
2．二次函数的部分图像如图所示，可知方程的所有解的积为（ ）
A．－4B．4C．5D．－5
【答案】D
【解析】解：由图象可知对称轴为，与x轴的一个交点横坐标是5，
∵交点到对称轴的距离是3个单位，
∴另外一个交点的横坐标是﹣1，
∴.
故选：D.
3．已知抛物线y＝ax2＋bx＋c（a≠0）的顶点为（2，4），有以下结论：①当a>0时，b2－4ac>0；②当a>0时，ax2＋bx＋c≥4；③若点（-2，m）,（3，n）在抛物线上，则m