必考专题：圆柱与圆锥应用题-数学六年级下册北师大版

这是一份必考专题：圆柱与圆锥应用题-数学六年级下册北师大版，共19页。试卷主要包含了一个圆柱形铁皮水桶等内容，欢迎下载使用。

2．如图，这个瓶子净含量是750mL，瓶子里装满了矿泉水，小刚喝了一些后，把瓶盖拧紧后倒置放平，小刚喝了多少mL的水？
3．慧慧家有一根长720厘米的铁条和一些铁皮，准备用这根铁条焊接成一个长方体框架并加工成养花盆。家里在讨论时，爸爸说：按长宽高的比为3∶2∶1焊接框架好看，慧慧说：按长宽高的比为3∶2∶2焊接框架好看，妈妈说：不能浪费铁条，而且为了不让花盆氧化需要在里外都刷上油漆，慧慧说：我想在花盆里放一个最大的圆柱玻璃鱼缸养鱼。你觉得她们家的花盆要刷多少面积的铁皮？最多还能装多少泥土？（铁皮厚度忽略不计）
4．如图，下面是张娜测量一块石头体积时的情景，根据图中信息，计算石头的体积。（图中单位：厘米）
5．一种圆柱形易拉罐饮料外部尺寸如图1，在运输中一般按图2的包装方法包装，每个包装箱正好装18瓶饮料。
（1）包装箱长、宽、高分别是∶（________厘米、________厘米、________厘米。）
（2）每个包装箱（无盖，上面是塑料薄膜）至少需要多少平方厘米的纸板？
（3）商场进货价是72元/箱，订货50箱以上（含50箱）的，还可以享受九五折优惠，现商场一次性订货60箱，然后按一瓶6.5元出售。每卖1瓶饮料，还需要人工，场租金等开支1.2元，这批饮料卖完后净可赚多少元？
6．一个圆柱形粮囤，从里面量底面直径是3米，高2米。如果每立方米稻谷重650千克，这个粮囤大约能装多少吨稻谷？（结果保留两位小数）
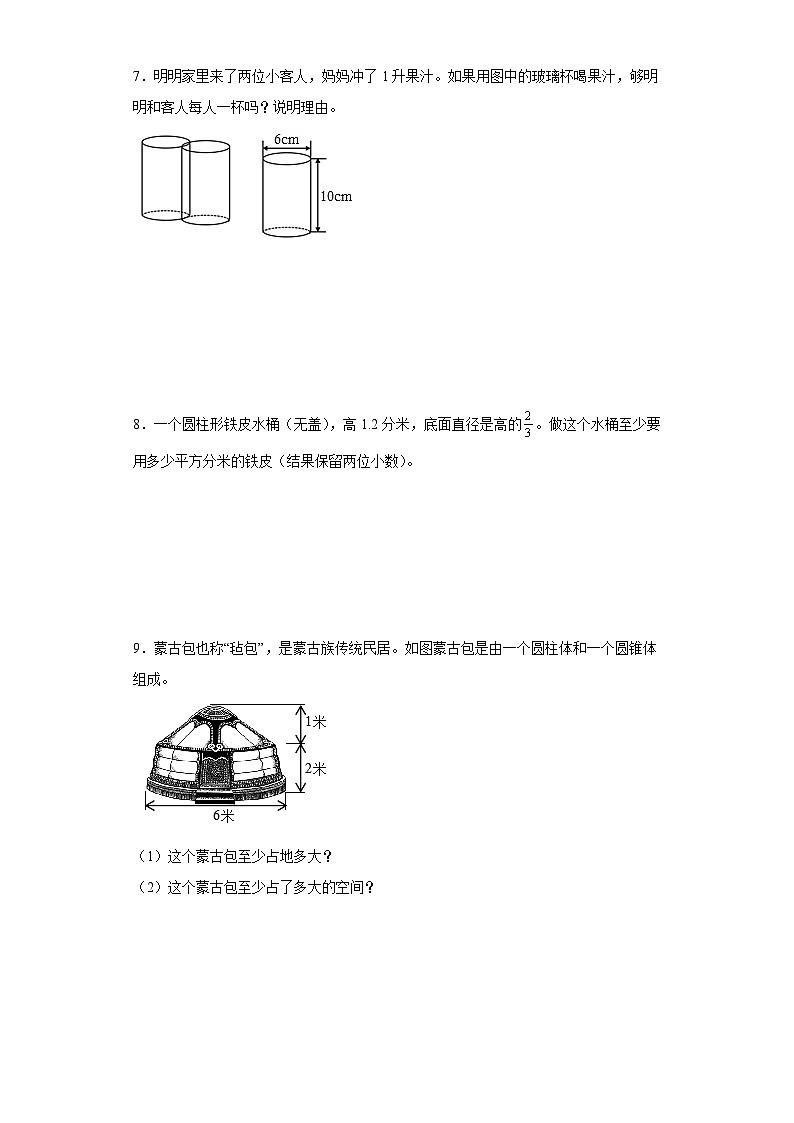
7．明明家里来了两位小客人，妈妈冲了1升果汁。如果用图中的玻璃杯喝果汁，够明明和客人每人一杯吗？说明理由。
8．一个圆柱形铁皮水桶（无盖），高1.2分米，底面直径是高的。做这个水桶至少要用多少平方分米的铁皮（结果保留两位小数）。
9．蒙古包也称“毡包”，是蒙古族传统民居。如图蒙古包是由一个圆柱体和一个圆锥体组成。
（1）这个蒙古包至少占地多大？
（2）这个蒙古包至少占了多大的空间？
10．一个正方体玻璃鱼缸从内测量棱长是5分米，水深3分米。李明现在将一个底面积是12.5平方分米的圆锥装饰物放入鱼缸，完全浸没在水中，这时水面上升了2厘米，这个圆锥装饰物的高是多少？
11．一个圆柱，底面直径是8厘米，侧面沿高展开得到一个宽是12厘米的长方形。分别求出这个圆柱的表面积和体积。
12．沙漏是古人用的一种计时仪器。下面这个沙漏里（装满沙子）的沙子一点点漏入下面空着的长方体木盒中，若沙子漏完了，均匀地铺在盒子中，那么在长方体木盒中会铺上大约多少厘米高的沙子呢？（结果保留两位小数）
13．有两块铁皮，如下图所示，用它们做一个最大的无盖圆柱形铁皮水桶。
①请通过计算说明，左边这个边长4dm的正方形铁皮，能做成这个水桶的底面吗？
②如果要给这个水桶的里外都涂上防锈漆，涂漆的面积是多少平方分米？（接头处不计）
14．下图平行线之间两个圆及一块长方形正好可以做成一个圆柱体，这个圆柱体的底面半径3分米，那么圆柱的体积是多少立方分米？
15．神舟十三号飞船的飞行目标是对接我国空间站“天和”核心舱，将三名航天员运送至中国空间站。神舟十三号乘组人员在空间站工作和生活六个月，创造了我国航天员在太空驻留天数的新纪录。飞船主体由轨道舱、返回舱和推进舱构成。轨道舱主体为圆柱形，集工作、吃饭和睡觉等诸多功能于一体，总长度为2米，直径约2.2米（如图），它的体积大约是多少？（得数保留一位小数）
16．一根自来水管的内直径是2厘米，水管内水流速度为每秒10厘米。如果洗手后忘记关水龙头，10分才发现，这期间浪费了多少升水？
17．一堆9.8方的沙子装入到一个高1.8米的圆柱形容器里，露出的部分是一个高0.9米的圆锥形沙堆，这个圆锥形沙堆的体积是多少立方米？（1方等于1立方米）
18．如图，把一个底面半径是2分米、高是6分米的圆柱形木料，削成一个由两个圆锥体组成的零件。每个圆锥的高是原来圆柱高的一半，底面积和原来圆柱的底面积相等。求削去部分的体积。（取3.14）
19．小明的妈妈榨了一些果汁，贮存在一个长方体容器中，果汁的高度为15厘米。小明将果汁往内直径6厘米、深10厘米的圆柱形玻璃杯中倒了满满一杯后，长方体容器中果汁的高度降至12厘米，这时长方体容器中的果汁大约还有多少升？（保留一位小数）
20．袁隆平爷爷，世界上第一个成功利用水稻杂交优势的科学家，被誉为“杂交水稻之父”，发展杂交水稻，造福世界人民是袁隆平院士毕生的追求。目前，我国杂交水稻年种植积约2.57亿亩，非杂交水稻年种植面积约1.94亿亩，2020年我国稻谷总产量约为120亿千克，其中杂交水稻产量与非杂交水稻产量的比为13∶7，杂交水稻每年增产的稻谷，可为中国多养活8000万人。
（1）2020年杂交水稻产量约多少亿千克？
（2）根据上面的信息，如果列式为，那么问题为___________________。
（3）如下图，已知圆锥形谷堆的底面直径是圆柱形铁桶底面直径的2倍，它们的高一样，把这些稻谷装在铁桶中（铁桶厚度忽略不计），装得下吗？请把你的想法写下来。
参考答案：
1．25.8立方分米
【分析】正方体内最大圆柱体的底面直径和高等于正方体的棱长，把正方体的棱长设为未知数，根据“”求出正方体的体积，削去部分的体积＝正方体的体积－最大圆柱的体积，据此解答。
【详解】解：设正方体的棱长为a分米。
3.14×（a）2×a＝94.2
（a）2×a＝94.2÷3.14
（a）2×a＝30
a3＝30
a3＝30÷
a3＝120
由上可知，正方体的体积是120立方分米。
削去部分的体积：120－94.2＝25.8（立方分米）
答：削去部分的体积是25.8立方分米。
【点睛】利用方程根据圆柱的体积计算公式求出正方体的体积是解答题目的关键。
2．500mL
【分析】因为原来瓶是装满水的，所以喝的水量就是倒置后无水部分的体积，根据圆柱体的体积公式：V＝Sh，h＝5＋10＝15（cm），将数据代入计算，求出S，再计算出倒置后无水部分的体积，即可得解。
【详解】750mL＝750cm3
750÷15＝50（cm2）
50×10＝500（cm3）
500cm3＝500mL
答：小刚喝了500mL。
【点睛】此题解答关键是先求出矿泉水瓶的底面积，要明白倒置后无水部分的体积就是所喝水的体积。
3．28800平方厘米；77220立方厘米
【分析】首先求出长方体框架长、宽、高的和，再确定按哪种比分配能使长、宽、高都是整数；花盆在里外都刷上油漆，就是求长方体四个侧面与－个底面的面积和的2倍；用长方体花盆的体积减去以长方形的宽为直径且与长方体等高的圆柱的体积。
【详解】720÷4＝180（厘米）
若按长、宽、高的比为3∶2∶1，则将180厘米平均分成6份，180是6的倍数，长、宽、高都是整数。
若按长、宽、高的比为3∶2∶2，则将180厘米平均分成7份，180不是7的倍数，长、宽、高都不是整数。
所以应该按长、宽、高的比为3∶2∶1，确定长、宽、高。
180×＝90（厘米）
180×＝60（厘米）
180×＝30（厘米）
90×60＋90×30×2＋60×30×2
＝5400＋2700×2＋1800×2
＝5400＋5400＋3600
＝10800＋3600
＝14400（平方厘米）
14400×2＝28800（平方厘米）
90×60×30
＝5400×30
＝162000（立方厘米）
3.14×（60÷2）2×30
＝3.14×900×30
＝2826×30
＝84780（立方厘米）
162000－84780＝77220（立方厘米）
答：花盆要刷28800平方厘米的铁皮，最多还能装77220立方厘米的泥土。
【点睛】本题考查了按比例分配、长方体的棱长和、长方体的表面积、长方体的体积、圆柱体的体积，综合性强，需认真分析解答。
4．157立方厘米
【分析】先求出底面半径为5厘米，把石头放入水中后，水面上升了（10－8）厘米，石头的体积相当于水面上升的体积，这部分体积可看作底面积为（3.14×52）平方厘米，高为（10－8）厘米的圆柱的体积，根据圆柱的体积公式：V＝Sh，代入数据即可得解。
【详解】3.14×（10÷2）2×（10－8）
＝3.14×52×2
＝3.14×25×2
＝157（立方厘米）
答：石头的体积是157立方厘米。
【点睛】此题的解题关键是掌握求不规则物体体积的计算方法，灵活运用圆柱的体积公式求解。
5．（1）36；18；12；（2）1944平方厘米；（3）1620元
【分析】（1）包装箱的长是6个易拉罐的底面直径的总长，宽是3个易拉罐的底面直径总长，高是易拉罐的高；
（2）求包装箱5个面的面积和，利用公式包装箱表面积＝长×宽＋长×高×2＋宽×高×2计算即可；
（3）一箱饮料18瓶，利用数量乘单价乘折扣求出进货的总价格，然后利用每瓶的卖价减去人工租金的价格的差再乘每箱的数量，然后乘箱数最后减去进货的总价就是赚的钱数。
【详解】6×6＝36（厘米）
6×3＝18（厘米）
答：包装箱长、宽、高分别是：36厘米、18厘米、12厘米。
（2）36×18＋36×12×2＋18×12×2
＝648＋864＋432
＝1944（平方厘米）
答：至少需要1944平方厘米的纸板。
（3）72×60×95%
＝4320×95%
＝4104（元）
（6.5−1.2）×18
＝5.3×18
＝95.4（元）
95.4×60＝5724（元）
5724−4104＝1620（元）
答：这批饮料卖完后净可赚1620元。
【点睛】本题考查了长方体的表面积公式的应用及数量、单价总价的之间关系的应用。
6．9.18吨
【分析】根据圆柱的体积（容积）公式：V＝πr2h，把数据代入公式求出这个粮囤的容积（稻谷的体积），然后用稻谷的体积乘每立方米稻谷的质量即可。
【详解】3.14×（3÷2）2×2×650
＝3.14×2.25×2×650
＝9184.5（千克）
9184.5千克≈9.18吨
答：这个粮囤能装9.18吨稻谷。
【点睛】此题主要考查圆柱的体积（容积）公式的灵活运用，关键是熟记公式。
7．够；理由见详解。
【分析】根据题意，圆柱的底面半径为（6÷2）厘米，高为10厘米，利用圆柱的体积（容积）公式：V＝代入即可求出其中1个玻璃杯的容积，再乘3得出3个玻璃杯的容积，换算单位后与1升果汁比较大小，如果小于1升果汁，说明够明明和客人每人一杯，反之则不够明明和客人每人一杯。
【详解】3.14×（6÷2）²×10×3
＝3.14×3²×10×3
＝3.14×9×10×3
＝282.6×3
＝847.8（立方厘米）
847.8立方厘米＝847.8毫升
1升＝1000毫升
847.8毫升＜1升
答：够明明和客人每人一杯。因为果汁的体积大于3个杯子能容纳液体的最大体积。
【点睛】此题的解题关键是灵活运用圆柱的体积（容积）公式求解。注意换算单位。
8．3.02平方分米
【分析】将高看作单位“1”，高×底面直径对应分率＝底面直径，用底面积＋侧面积＝需要的铁皮面积，据此列式解答。
【详解】1.2×＝0.8（分米）
3.14×0.42＋0.8×3.14
＝3.14×0.16＋2.512
＝0.5024＋2.512
＝3.0144
≈3.02（平方分米）
答：做这个水桶至少要用3.02平方分米的铁皮。
【点睛】关键是理解分数乘法的意义，掌握并灵活运用圆柱表面积公式。
9．（1）28.26平方米
（2）65.94立方米
【分析】（1）求蒙古包的占地面积，实际上就是求圆柱的底面积，底面直径已知，从而可以求出底面积；
（2） 蒙古包所占空间就等于圆锥与圆柱的体积和，底面直径和圆锥与圆柱的高已知，从而可以求解。
【详解】（1）3.14×（6÷2）2
＝3.14×9
＝28.26（平方米）
答：这个蒙古包至少占地28.26平方米。
（2）28.26×2＋28.26×1×
＝56.52＋9.42
＝65.94（立方米）
答：这个蒙古包至少占了65.94立方米的空间。
【点睛】此题主要考查圆的面积、圆锥和圆柱的体积计算方法，解答时要弄清楚有关数据的长度。
10．1.2分米
【分析】圆锥装饰物放入鱼缸后，先换算单位，水面上升的高度为0.2分米，圆锥装饰物的体积等于水面上升的体积，水面上升的体积可看作长宽均为5分米，高为0.2分米的长方体的体积，根据长方体的体积公式：V＝abh，代入数据即可求出这个圆锥装饰物的体积，再利用圆锥的体积公式：V＝Sh，用圆锥装饰物的体积除以圆锥的底面积，即可求出这个圆锥装饰物的高。
【详解】2厘米＝0.2分米
5×5×0.2÷÷12.5
＝5÷÷12.5
＝15÷12.5
＝1.2（分米）
答：这个圆锥装饰物的高是1.2分米。
【点睛】此题的解题关键是掌握求不规则物体的体积的计算方法，通过转化的数学思想，灵活运用长方体的体积和圆锥的体积公式求解。
11．表面积：401.92平方厘米；
体积：602.88立方厘米
【分析】根据圆柱侧面展开图的特征，圆柱的侧面沿高展开是一个长方形。这个长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高，根据圆柱的表面积＝侧面积＋底面积×2，圆柱的侧面积＝底面周长×高，圆的面积公式：S＝πr2，圆柱的体积公式：V＝πr2h，把数据代入公式解答。
【详解】3.14×8×12＋3.14×（8÷2）2×2
＝25.12×12＋3.14×16×2
＝301.44＋50.24×2
＝301.44＋100.48
＝401.92（平方厘米）
3.14×（8÷2）2×12
＝3.14×16×12
＝50.24×12
＝602.88（立方厘米）
答：圆柱的表面积是401.92平方厘米，体积是602.88立方厘米。
【点睛】此题主要考查圆柱的表面积公式、体积公式的灵活运用，关键是熟记公式。
12．0.63厘米
【分析】根据圆锥体积＝底面积×高÷3，求出沙子体积，再根据长方体的高＝体积÷底面积，列式解答即可，注意统一单位。
【详解】3.14×（1.2÷2）2×1÷3
＝3.14×0.62×1÷3
＝3.14×0.36×1÷3
＝0.3768（立方分米）
0.3768÷（3×2）
＝0.3768÷6
＝0.0628（分米）
≈0.63（厘米）
答：长方体木盒中会铺上大约0.63厘米高的沙子。
【点睛】关键是掌握并灵活运用圆锥和长方体体积公式。
13．①能；计算见详解
②175.84平方分米
【分析】①只要水桶的底面直径不超过正方形的边长，就可做成这个水桶的底面，根据直径＝周长÷π，列式计算即可。
②涂漆的面积＝底面积×2＋侧面积×2，据此列式解答。
【详解】①12.56÷3.14＝4（分米）
答：能做成这个水桶的底面。
②4÷2＝2（分米）
3.14×22×2＋12.56×6×2
＝3.14×4×2＋150.72
＝25.12＋150.72
＝175.84（平方分米）
答：涂漆的面积是175.84平方分米。
【点睛】关键是熟悉圆柱特征，掌握并灵活运用圆柱表面积公式。
14．169.56立方分米
【分析】观察可知，圆柱的高＝底面直径，根据圆柱体积＝底面积×高，列式解答即可。
【详解】r＝3（分米）
h＝3×2＝6（分米）

（立方分米）
答：那么圆柱的体积是169.56立方分米。
【点睛】关键是看懂图示，掌握并灵活运用圆柱体积公式。
15．7.6立方米
【分析】根据圆柱的体积公式：V＝πr2h，据此代入数值进行计算即可。
【详解】3.14×（2.2÷2）2×2
＝3.14×1.12×2
＝3.7994×2
≈7.6（立方米）
答：它的体积大约是7.6立方米。
【点睛】本题考查圆柱的体积，熟记公式是解题的关键。
16．18.84升
【分析】由题意可知，把水的体积看作是一个圆柱形，根据速度×时间＝路程，据此求出水的高度，然后根据圆柱的体积公式：V＝πr2h，据此代入数值进行计算即可。
【详解】10分＝600秒
3.14×（2÷2）2×（10×600）
＝3.14×1×6000
＝18840（立方厘米）
＝18.84（立方分米）
＝18.84（升）
答：这期间浪费了18.84升水。
【点睛】本题考查圆柱的体积，熟记公式是解题的关键。
17．1.4立方米
【分析】观察图形，圆锥的底面积和圆柱的底面积相等，可设为，利用圆柱的体积公式：V＝，h＝1.8米，代入表示出圆柱的体积，利用圆锥的体积公式：V＝，h＝0.9米，代入表示出圆锥的体积，圆柱的体积＋圆锥的体积＝9.8，求出，再通过圆锥的体积公式求出这个圆锥形沙堆的体积。
【详解】
由可得：
（立方米）
答：圆锥形沙堆的体积是1.4立方米。
【点睛】此题的解理关键是认识到圆柱和圆锥的底面积相等并通过体积公式求出底面积，再根据圆锥的体积公式即可得解。
18．50.24立方分米
【分析】等底等高的圆柱和圆锥，圆柱体积是圆锥体积的3倍，削去部分的体积是圆柱体积的（1－），根据圆柱体积＝底面积×高，圆柱体积×削去部分对应分率＝削去部分的体积，据此列式解答。
【详解】3.14×22×6×（1－）
＝3.14×4×6×
＝50.24（立方分米）
【点睛】关键是掌握并灵活运用圆柱体积公式，理解圆柱和圆锥体积之间的关系。
19．1.1升
【分析】根据圆柱的容积公式：V＝πr2h，据此求出圆柱形玻璃杯中果汁的体积，此果汁的体积就是高为15－12＝3厘米长方体的容积，然后根据长方体的容积公式：V＝Sh求出长方体容器的底面积，进而求出此时长方体容器中剩下的果汁的升数。
【详解】3.14×（6÷2）2×10÷（15－12）
＝3.14×9×10÷3
＝282.6÷3
＝94.2（平方厘米）
94.2×12＝1130.4（立方厘米）＝1.1304（立方分米）≈1.1（升）
答：这时长方体容器中的果汁大约还有1.1升。
【点睛】本题考查圆柱和长方体的容积，熟记公式是解题的关键。
20．（1）78亿千克；（2）非杂交水稻年种植面积占我国杂交水稻年种植面积的几分之几？（3）装不下，详细过程见详解
【分析】（1）根据分数乘法的意义，用2020年我国稻谷总产量乘杂交水稻产量占稻谷总产量的几分之几，据此解答；
（2）1.94亿亩表示非杂交水稻年种植面积，2.57亿亩表示我国杂交水稻年种植面积，算式表示非杂交水稻年种植面积占我国杂交水稻年种植面积的几分之几，据此提出问题；
（3）分别计算圆锥形谷堆的体积和圆柱体铁桶的体积，据此作出判断。
【详解】（1）
（亿千克）
答：2020年杂交水稻产量约78亿千克。
（2）根据上面的信息，如果列式为，那么问题为：非杂交水稻年种植面积占我国杂交水稻年种植面积的几分之几？
（3）圆柱体铁桶的体积：
＝3.14×2.25×1.8
=12.717（立方米）
圆锥形谷堆的体积：
（米）
（立方米）
因为12.717立方米16.956立方米，所以把这些稻谷装铁桶中，装不下。
答：铁桶装不下这些稻谷。
【点睛】解答本题的关键是理解比例分配应用题的解题方法，同时熟练掌握圆柱和圆锥体积的计算方法。