专题18-探索规律（考点聚焦+重点速记+真题专练）-2023-2024学年六年级备战小升初数学专项复习精讲练+（通用版）

这是一份专题18-探索规律（考点聚焦+重点速记+真题专练）-2023-2024学年六年级备战小升初数学专项复习精讲练+（通用版），共19页。试卷主要包含了算式中的规律，数列中的规律，数形结合规律，1612等内容，欢迎下载使用。

1、算式中的规律。
在数学算式中探索规律，应认真观察算式的特点，再观察结果的特点，进而，根据规律填出这一类算式的结果．
例如：1×1=1；
11×11=121；
111×111=12321；
1111×1111=1234321；
通过观察发现：每个算式中，两个因数各个数位上的数字都是1，且个数相同．积里的数字呈对称形式，且前半部分是从1开始，写至某个数字（此数即因数的位数），积的后半部分再顺次写出．
2、数列中的规律。
按一定的次序排列的一列数，叫做数列．
（1）规律蕴涵在相邻两数的差或倍数中．
例如：1，2，3，4，5，6…相邻的差都为1；
1，2，4，8，16，32…相邻的两数为2倍关系．
（2）前后几项为一组，以组为单位找关系，便于找到规律．
例如：1，0，0，1，1，0，0，1…从左到右，每四项为一组；
1，2，3，5，8，13，21…规律为，从第三个数开始，每个数都是它前面两个数的和．
（3）需将数列本身分解，通过对比，发现规律．
例如，12，15，17，30，22，45，27，60…在这里，第1，3，5…项依次相差5，第2，4，6…项依次相差15．
（4）相邻两数的关系中隐含着规律．
例如，18，20，24，30，38，48，60…相邻两数依次差2，4，6，8，10，12…
3、数形结合规律。
在探索数与形结合的规律时，一方面要考虑图形的对称（上下对称和左右对称），另一方面要考虑数的排列规律，通过数形结合、对应等方法，来解决问题．
小升初真题复习—探索规律
一．选择题（共8小题，满分16分，每小题2分）
1．（2分）（2023•郑州）如图，〇、△、□各表示一个两位数中的其中一个数字，观察下面图与数的关系，第4图形表示的两位数是（ ）
A．54B．43C．34
2．（2分）（2023•临西县）瑞士的巴尔末从测量光谱的数据95、1612、2521、3632⋯⋯中得到了巴尔末公式，请你按这种规律写出第10个数据，这个数据为（ ）
A．8177B．10096C．144140D．10098
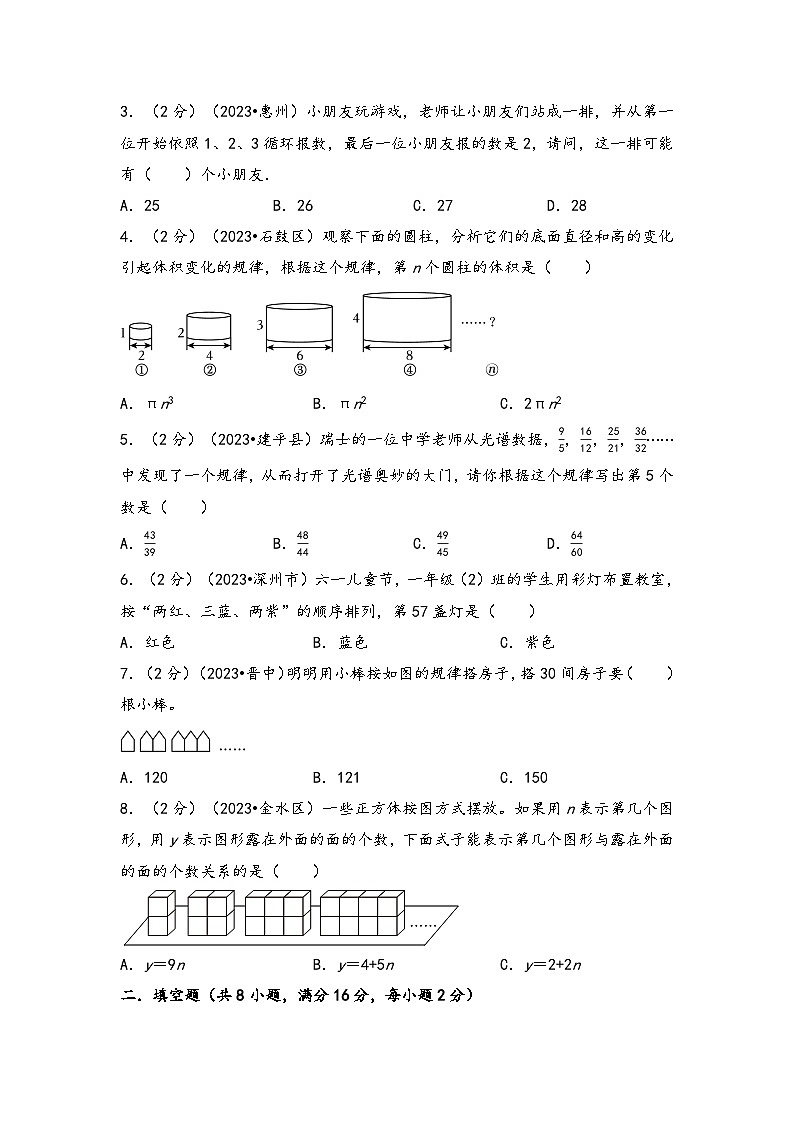
3．（2分）（2023•惠州）小朋友玩游戏，老师让小朋友们站成一排，并从第一位开始依照1、2、3循环报数，最后一位小朋友报的数是2，请问，这一排可能有（ ）个小朋友．
A．25B．26C．27D．28
4．（2分）（2023•石鼓区）观察下面的圆柱，分析它们的底面直径和高的变化引起体积变化的规律，根据这个规律，第n个圆柱的体积是（ ）
A．πn3B．πn2C．2πn2
5．（2分）（2023•建平县）瑞士的一位中学老师从光谱数据，95，1612，2521，3632⋯⋯中发现了一个规律，从而打开了光谱奥妙的大门，请你根据这个规律写出第5个数是（ ）
A．4339B．4844C．4945D．6460
6．（2分）（2023•深州市）六一儿童节，一年级（2）班的学生用彩灯布置教室，按“两红、三蓝、两紫”的顺序排列，第57盏灯是（ ）
A．红色B．蓝色C．紫色
7．（2分）（2023•晋中）明明用小棒按如图的规律搭房子，搭30间房子要（ ）根小棒。
A．120B．121C．150
8．（2分）（2023•金水区）一些正方体按图方式摆放。如果用n表示第几个图形，用y表示图形露在外面的面的个数，下面式子能表示第几个图形与露在外面的面的个数关系的是（ ）
A．y＝9nB．y＝4+5nC．y＝2+2n
二．填空题（共8小题，满分16分，每小题2分）
9．（2分）（2023•涵江区）将一些小圆球如图摆放，第9幅图中共有 个小圆球。
10．（2分）（2023•金昌）用大小一样的圆形画图，先观察前四幅图阴影部分面积与1个圆面积的关系，再根据这个规律推算第五幅图阴影部分的面积相当于 个圆的面积。
11．（2分）（2023•荔城区）如果按照如图正方形点子图的规律排列，第⑥幅图共有 个点子，第n幅图共有 个点子。
12．（2分）（2023•万州区）找规律，填一填。△□□〇〇☆△□□〇〇☆△□□〇〇☆……第40个图形是 。
13．（2分）（2023•化州市）如图，用小棒摆正方形。摆1个正方形要4根小棒，摆2个正方形要7根小棒，继续这样摆，摆10个正方形要 根小棒；摆n个正方形需要的小棒根数是 根。
14．（2分）（2023•平湖市）如图所示，第1层有1个点，第2层有4个点，第3层有9个点……按这样的规律，第9层有 个点，第 有196个点。
15．（2分）（2023•信阳）如图，按照前面四幅图的规律，算出第五幅图中的正方形里共有 个圆；再算出第七幅图中的正方形里共有 个圆。
16．（2分）（2023•莆田）有一列由两个数组成的数组：（1，1），（2，1），（2，2），（3，1），（3，2），（3，3），（4，1），（4，2），（4，3），（4，4），（5，1）……
①第72组的两个数之和是 。
②在前55组中，“5”这个数出现了 次。
三．判断题（共4小题，满分8分，每小题2分）
17．（2分）（2023•高阳县）△△△▽▼△△△▽▼……，照这样排列下去，第30个图形一定是▼。
18．（2分）（2023•通榆县）这组数据是没有规律的：3，10，18，27，37，48，60，……。
19．（2分）（2022•孟州市）下面是一组按规律排列的数：60、75、90、105、120……则935不是这组数中的数。
20．（2分）（2022•昆明）用小棒按如图搭三角形，搭一个用3根小棒，搭两个用5根小棒，搭n个用3n根小棒。
四．应用题（共7小题，满分60分）
21．（6分）（2023•罗甸县）像如图那样用小棒摆三角形，请你算一算。摆10个三角形用多少根小棒？摆n个三角形呢？
22．（6分）（2021•越城区）有一个无限小数，小数部分任意相邻四位数字之和都是26，已知第3位是3，第6位是6，第8位是8，那么第2021位上的数字是几？（写出计算与分析过程）
23．（6分）（2021•黔南州）如图，1个杯子的高度是15cm，把5个完全一样的杯子叠起来的高度是25cm，那么10个这样的杯子叠起来的高度是多少厘米？
24．（8分）（2023•临西县）一张长方形桌子可坐6人，按如图方式将桌子拼在一起。
（1）2张这样的桌子拼在一起可坐多少人？3张桌子呢？n张桌子呢？
（2）一家饭店有80张这样的长方形桌子，按照如图方式每4张拼成1张大桌子，则80张桌子可拼成20张大桌子，共可坐多少人？
25．（10分）（2023•武城县）如图所示，用“十字”分割正方形。分割一次，分成了4个正方形，分割两次，分成了7个正方形。
（1）如果连续用“十字”分割4次，分成了 个正方形。
（2）如果连续用“十字”分割n次，会分成 个正方形。
（3）如果分成346个正方形。需要用“十字”分割 次。
26．（12分）（2023•东山区）（1）用一个长方形像图中那样任意圈出四个数字，你发现了什么规律？
（2）如果长方形中最上面一个数字用a表示，最下面一个数字可以怎样表示？
（3）按这样的圈法，小丽圈出的四个数的和是200，你知道她圈的是哪四个数吗？算一算写出来。
27．（12分）（2022•高邑县）聪聪和明明在研究两个平方数的差时发现了规律：
42﹣22＝（4+2）×（4﹣2）＝12
72﹣32＝（7+3）×（7﹣3）＝40
92﹣42＝（9+4）×（9﹣4）＝65
（1）请你根据聪聪和明明发现的规律把下面的算式填写完整。
152﹣52＝（ + ）×（ ﹣ ）＝（ ）
（2）求如图中阴影部分的面积。聪聪说可以用“a2﹣b2”来计算，明明说也可以用“（a+b）×（a﹣b）”来计算。你知道明明是怎么想的吗？
参考答案
一．选择题（共8小题，满分16分，每小题2分）
1．【分析】前3个图中都有圆，表示的数字中都有5，即5表示圆形；进而可以得出3表示三角形；4表示正方形；而且第一个数字表示的图形在外面，第二个数字表示图形在第一个数字表示图形的里面．
【解答】解：图形中有一个正方形和一个三角形，正方形在外，三角形在内，所以用数字：43表示．
故选：B．
【分析】根据第一幅、第二幅和第三幅图中的数字，得出：〇△□各表示的数字是解决本题的关键．
2．【分析】根据所给数据发现：分子是从3开始的数的平方，分母比分子小4。据此解答。
【解答】解：3+（10﹣1）＝12
12×12＝144
144﹣4＝140
所以第10个数据为144140。
故选：C。
【分析】通过观察、分析、归纳发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力。
3．【分析】根据题意，每3个小朋友一循环，因为最后一个报的是2，所以小朋友的个数应该是3的倍数多2人．分别计算各选项人数，即可找到符合题意的选项。
【解答】解：25÷8＝3（组）……1（个）
26÷3＝8（组）……2（个）
27÷3＝9（组）
28÷3＝9（组）……1（个）
所以26个小朋友最后一个报数是2。
答：这一排可能有26个小朋友。
故选：B。
【分析】先找到规律，再根据规律求解。
4．【分析】利用圆柱的体积公式：V＝πr2h计算前面几个圆柱的体积，根据体积的变化发现规律，并运用规律做题。
【解答】解：①π×（2÷2）2×1＝π
②π×（4÷2）2×2＝8π＝23π
③π×（6÷2）2×3＝27π＝33π
所以第n个圆柱的体积是πn3。
故选：A。
【分析】本题考查了图形的变化类问题，主要培养学生的观察能力和总结能力。
5．【分析】观察可知，分子是3、4、5、6……的平方数，分母比分子小4，第5个数的分子是7的平方，据此解答即可。
【解答】解：72＝49
49﹣4＝45
答：根据这个规律写出第5个数是4945。
故选：C。
【分析】本题考查了数字的变化规律，知道分子和分母的变化规律是解题关键。
6．【分析】由题意可知，循环周期是7，用57除以循环周期，计算出商和余数，找出第57盏灯是什么颜色即可。
【解答】解：57÷7＝8（组）……1（盏）
答：第57盏灯是红色。
故选：A。
【分析】本题考查了简单的周期现象，找出循环周期是几是解题的关键。
7．【分析】搭一间房用5根小棒，2间房用9根小棒，3间房用13根小棒，以后每增加一间房就多用4根小棒，由此解决问题。
【解答】解：搭一间房用5根小棒，可以写成1+1×4；
2间房用9根小棒，可以写成1+2×4；
3间房用13根小棒，可以写成1+3×4；
……
所以搭n间房子需要1+4n根小棒。
当n＝30时，需要小棒1+30×4＝121（根）
答：搭30间房子要121根小棒。
故选：B。
【分析】主要考查了通过特例分析从而归纳总结出一般结论的能力．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的。
8．【分析】由图可知，第1个图形露出9个面，第2个图形露出14个面，第3个图形露出19个面，第4个图形露出24个面……，4个图形的左右两边都是露出4个面，每增加2个小正方体，就会增加5个面，据此找规律解答。
【解答】解：由分析可知，图形露在外面的面的个数＝5+图形的序数×5，如果用n表示第几个图形，用y表示图形露在外面的面的个数，则y＝4+5n。
故选：B。
【分析】解答本题需准确分析图形的序数与露出的面数之间的关系，分析出每增加2个小正方体，就会增加5个面是关键。
二．填空题（共8小题，满分16分，每小题2分）
9．【分析】由图可知，第1个图形有1个小圆球，第2个图形有（1+3）个小圆球，第3个图形有（1+3+5）个小圆球，第4个图形有（1+3+5+7）个小圆球……以此类推，第n个图形小圆球的个数等于从1开始连续n个奇数的和，从1开始连续n个奇数的和等于奇数个数的平方，据此解答。
【解答】解：1+3+5+7+9+11+13+15+17＝92＝81（个）
答：第9幅图中共有81个小圆球。
故答案为：81。
【分析】本题主要考查数形结合思想的应用，找出小圆球个数的变化规律是解答题目的关键。
10．【分析】观察图示可知：阴影部分是由几个扇形组成的，且扇形的半径与所在圆的半径相等，扇形内角和可通过三角形内角和、四边形内角和推得，扇形的面积由半径和圆心角决定，据此可推算出第五幅图阴影部分的面积相当于几个圆的面积。
【解答】解：①三角形内角和为180°，阴影部分由三个扇形组成，扇形半径与圆的半径相等，每个扇形的圆心角均是三角形的一个内角，三个圆心角的和就等于三角形内角和180°，则S阴影=180°360°×S圆=12S圆；
②四边形内角和为360°，阴影部分由四个扇形组成，扇形半径与圆的半径相等，每个扇形的圆心角均是四边形的一个内角，四个圆心角的和就等于四边形内角和360°，则S阴影=360°360°×S圆＝S圆；
③四边形内角和为360°，阴影部分由四个扇形和一个半圆组成，扇形半径与圆的半径相等，每个扇形的圆心角均是四边形的一个内角，四个圆心角的和就等于四边形内角和360°，再加上一个半圆圆心角为180°，则S阴影=360°+180°360°×S圆=32S圆；
④四边形内角和为360°，阴影部分由四个扇形和两个半圆组成，扇形半径与圆的半径相等，每个扇形的圆心角均是四边形的一个内角，四个圆心角的和就等于四边形内角和360°，再加上两个半圆圆心角之和为360°，则S阴影=360°+360°360°×S圆＝2S圆；
⑤四边形内角和为360°，阴影部分由四个扇形和三个半圆组成，扇形半径与圆的半径相等，每个扇形的圆心角均是四边形的一个内角，四个圆心角的和就等于四边形内角和360°，再加上三个半圆圆心角之和180°×3＝540°，则S阴影=360°+540°360°×S圆=52S圆。
答：第五幅图阴影部分的面积相当于52个圆的面积。
故答案为：52。
【分析】本题考查了图形变化的规律，需要对于多边形内角和比较熟悉，同时能够准确计算扇形的面积，还要善于发现图形之间的联系，找到变化的规律。
11．【分析】根据观察，第一幅有4个点子；
第二幅有8个点子；
第三幅有12个点子；
所以第n幅有4n个点子。
【解答】解：如果按照如图正方形点子图的规律排列，第⑥幅图共有24个点子，第n幅图共有4n个点子。
故答案为：24，4n。
【分析】本题主要考查数与形结合的规律，发现每多1个图形就多4个点子是解本题的关键。
12．【分析】每6个图形一循环，计算第40个图形是第几组循环零几个，即可判断其形状。
【解答】解：40÷6＝6（组）……4（个）
答：第40个图形是〇。
故答案为：〇。
【分析】先找到规律，再根据规律求解。
13．【分析】摆1个正方形要4根小棒，摆2个正方形要（4+3）根小棒，摆3个正方形要（4+3+3）根小棒，摆n个正方形要[4+3×（n﹣1）]根小棒，由此解答本题即可。
【解答】解：由分析可知，摆10个正方形需要小棒：4+3×（10﹣1）
＝4+3×9
＝31（根）
摆n个正方形需要的小棒根数：4+3×（n﹣1）
＝4+3n﹣3
＝（3n+1）根
故答案为：31；（3n+1）。
【分析】解决本题的关键是找出题中的规律，利用规律去解答。
14．【分析】规律：每层的点数等于层数的平方；则第9层有点的个数＝92＝81，196＝14×14，则第14层有196个点。
【解答】解：9×9＝81（个）
196＝14×14
所以第14层有196个点。
答：第9层有81个点，第14层有196个点。
故答案为：81；14层。
【分析】本题考查了图形的变化类问题，主要培养学生的观察能力和总结能力。
15．【分析】规律：每个正方形里面圆的个数是平方数，所以第n幅图中的正方形里共有n2个圆。
【解答】解：5×5＝25（个）
7×7＝49（个）
答：第五幅图中的正方形里共有25个圆；第七幅图中的正方形里共有49个圆。
故答案为：25；49。
【分析】本题考查了图形的变化类问题，主要培养学生的观察能力和总结能力。
16．【分析】①观察数组的规律，第一个数是1的有1组，第一个数是2的有2组，第一个数是3的有3组，第一个数是4的有4组，……，因为1+2+3+4+……+11＝66组，所以从第67组开始，每组的第一个数是12，第67组是（12，1），依此类推，第72组是（12，6），两个数的和是12+6＝18；
②因为1+2+3+……+10＝55组，所以第55组恰好是（10，10），第一个数是5的有5组，即（5，1）、（5，2）、（5、3）、（5，4）、（5，5）。第二个数是5的只能是（5，5）、（6，5）、（7，5）、（8，5）、（9，5）、（10，5）出现了6次，所以“5”这个数出现了11次。据此解答。
【解答】解：①观察数组的规律，可知：
第一个数是1的有1组，
第一个数是2的有2组，
第一个数是3的有3组，
第一个数是4的有4组，
……，
又1+2+3+4+……+11＝66组，
所以从第67组开始，每组的第一个数是12，第67组是（12，1），第68组是（12，2），……，第72组是（12，6），两个数的和：12+6＝18；
答：第72组的两个数之和是18。
②因为1+2+3+……+10＝55组，所以第55组恰好是（10，10）
第一个数是5的有5组，即（5，1）、（5，2）、（5、3）、（5，4）、（5，5），出现了5次；
第二个数是5的只能是（5，5）、（6，5）、（7，5）、（8，5）、（9，5）、（10，5）出现了6次；
所以“5”这个数出现：5+6＝11（次）
答：在前55组中，“5”这个数出现了11次。
故答案为：①18，②11。
【分析】通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力。
三．判断题（共4小题，满分8分，每小题2分）
17．【分析】每5个图形一循环，计算第30个是第几组循环零几个，即可判断其形状。
【解答】解：30÷5＝6（组）
所以第30个图形一定是▼。原题说法正确。
故答案为：√。
【分析】先找到规律，再根据规律求解。
18．【分析】依次加7、8、9、10、11、12。
【解答】解：3，10，18，27，37，48，60，……。规律为依次加7、8、9、10、11、12。所以原题干表述错误。
故答案为：×。
【分析】通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题是应该具备的基本能力。
19．【分析】这组数每次递增15，所以用935减去60，看能否被15整除即，如果能整除就是，否则不是；据此解答。
【解答】解：75﹣60＝15，90﹣75＝15，……
所以这组数每次递增15，
（935﹣60）÷15≈58.33
所以，935不是这组数中的数。原题干表述正确。
故答案为：√。
【分析】此题考查了数列的规律，关键是求出每次递增的数。
20．【分析】搭一个三角形需要3根小棒，搭两个三角形需要5根小棒，搭三个三角形需要7根小棒，则知搭n个三角形需要（2n+1）根小棒。
【解答】解：用小棒按如图搭三角形，搭一个用3根小棒，搭两个用5根小棒，搭n个用（2n+1）根小棒。原题说法错误。
故答案为：×。
【分析】本题考查规律型问题中的图形变化问题，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的。
四．应用题（共7小题，满分60分）
21．【分析】根据图示发现：摆1个三角形需要小棒：（1+2）根；摆2个三角形需要小棒：（1+2+2）根；摆3个三角形需要小棒：（1+2+2+2）根；依此类推……摆n个三角形需要小棒：（2×n+1）根。据此解答。
【解答】解：摆n个三角形需要小棒：2×n+1＝（2n+1）根
当n＝10时，
2×10+1
＝20+1
＝21（根）
答：摆10个三角形用21根小棒；摆n个三角形用（2n+1）根小棒。
【分析】本题主要考查数与形结合的规律，解题关键是根据图示发现这组图形的规律，并运用规律解决问题。
22．【分析】小数部分任意相邻四位数字之和都是26，说明循环周期是4，第6位和第2位一样，第8位和第4位一样，用相邻四位数字之和减去（3+6+8）就是循环周期的第一个数字，据此求出一个循环周期的四位数字，再用2021除以循环周期，求出有几个循环周期零几个即可解答。
【解答】解：26﹣（3+6+8）
＝26﹣17
＝9
所以循环周期的四个数字是：9638；
2021÷4＝505……1
答：第2021位上的数字是9。
【分析】求出这个小数的循环节，找出循环周期是解题的关键。
23．【分析】1个杯子的高度是15cm，把5个完全一样的杯子叠起来的高度是25cm，那么上面每个杯子露出（25﹣15）÷4＝2.5（厘米），然后求出上面9个杯子露出的高度，再加上15厘米即可。
【解答】解：（25﹣15）÷4
＝10÷4
＝2.5（厘米）
2.5×（10﹣1）+15
＝22.5+15
＝37.5（厘米）
答：10个这样的杯子叠起来的高度是37.5厘米。
【分析】本题考查数和形中的找规律问题，找到共同特征解决问题即可。
24．【分析】（1）1张长方形桌子可坐6人，2张长方形桌子可坐（6+2）人，3张长方形桌子可坐（6+2+2）人，n张长方形桌子可坐[6+2×（n﹣1）]人，由此解答本题；
（2）先计算1张大桌子可坐多少人，然后计算20张大桌子，共可坐多少人。
【解答】解：（1）2张这样的桌子拼在一起可坐人数：6+2＝8（人）
3张这样的桌子拼在一起可坐人数：6+2+2＝10（人）
n张这样的桌子拼在一起可坐人数：6+2×（n﹣1）
＝6+2n﹣2
＝（2n+4）人
答：2张这样的桌子拼在一起可坐8人，3张桌子可坐10人，n张桌子可坐（2n+4）人。
（2）1张大桌子可坐人数：2×4+4
＝8+4
＝12（人）
12×20＝240（人）
答：共可坐240人。
【分析】解决本题的关键是找出题中的规律，利用规律去解答。
25．【分析】分割1次，分成了4个正方形，分割2次，分成了（4+3）个正方形，分割3次，分成了（4+3+3）个正方形，分割n次，分成了[4+3×（n﹣1）]个正方形，结合题意去解答即可。
【解答】解：（1）分割3次，分成的正方形的个数：4+3×（4﹣1）
＝4+9
＝13（个）
（2）分割n次，分成的正方形个数：4+3×（n﹣1）
＝4+3n﹣3
＝（3n+1）个
（3）3n+1＝346，则n＝115，所以需要分割115次。
故答案为：（1）13；（2）（3n+1）；（3）115。
【分析】解决本题的关键是找出题中的规律，利用规律去解答。
26．【分析】（1）圈出的4个数的个位数字相同，每相邻两个之间相差10。
（2）11+30＝41，34+30＝64……可得规律是a+30。
（3）第一个数与下面第二个数相差10，与下面第三个数相差20，与第四个数相差30。那么四个数的和减去（10+20+30）就是4个第一个数，第一个数可求，其余的即可求。
【解答】解：（1）圈出的4个数的个位数字相同，每相邻两个之间相差10；
（2）11+30＝41，34+30＝64……可得最下面的数字是：a+30。
（3）200﹣10﹣20﹣30＝140
140÷4＝35
这四个数是：35，45，55，65。
【分析】仔细观察，总结出规律是解决本题的关键。
27．【分析】（1）根据给出的两个平方数的差的算式，发现规律：两个数的平方差，等于这两个数的和乘这两个数的差。据此解答。
（2）因为正方形的面积＝边长×边长，两个正方形的边长分别为a、b，阴影部分的面积＝大正方形的面积﹣小正方形的面积，所以聪聪得出用“a2﹣b2”计算；而明明把阴影部分的图形进行了剪拼，重新组合成一个长为（a+b）、宽为（a﹣b）的长方形，根据长方形的面积＝长×宽，所以明明得出阴影面积也可以用“（a+b）×（a﹣b）“来计算。
【解答】解：（1）152﹣52＝（15+5）×（15﹣5）＝200
（2）阴影部分的面积＝大正方形的面积﹣小正方形的面积，即阴影部分的面积＝a2﹣b2。
明明的作法：明明把左图沿虚线剪开，把剪掉的小长方形拼到剩下的大长方形的右侧，重新拼接后的图形如下：
所以阴影部分的面积为：（a+b）×（a﹣b）。
故答案为：15，5，15，200。
【分析】找出算式的规律、数与形的规律以及运用规律解决实际问题是解题的关键。



……
4根
7根
10根小棒
……