




初中数学湘教版九年级下册2.2 圆心角、圆周角课前预习ppt课件
展开1.直径所对的圆周角是直角,90°的圆周角所对的弦是直径;2.圆内接四边形的对角互补.
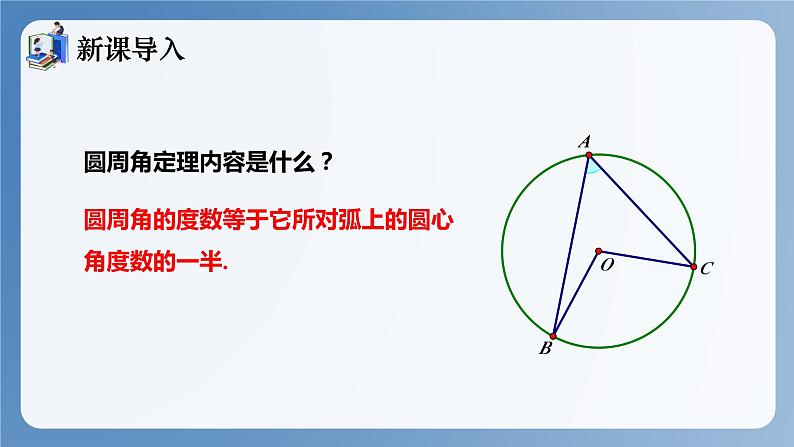
圆周角定理内容是什么?
圆周角的度数等于它所对弧上的圆心角度数的一半.
如图是一个圆形,给你一个三角板,你有办法确定这个圆形的圆心吗?
一 圆周角定理推论2
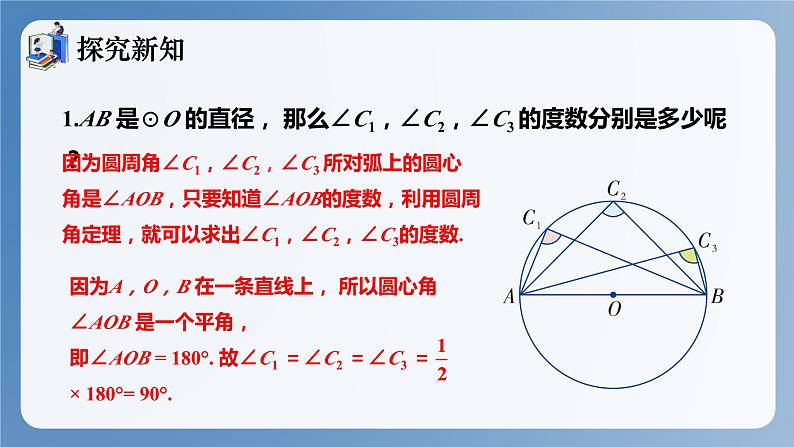
1.AB 是⊙O 的直径, 那么∠C1,∠C2,∠C3 的度数分别是多少呢?
因为圆周角∠C1,∠C2,∠C3 所对弧上的圆心角是∠AOB,只要知道∠AOB的度数,利用圆周角定理,就可以求出∠C1,∠C2,∠C3的度数.
因为A,O,B 在一条直线上, 所以圆心角∠AOB 是一个平角,即∠AOB = 180°. 故∠C1 =∠C2 =∠C3 = × 180°= 90°.
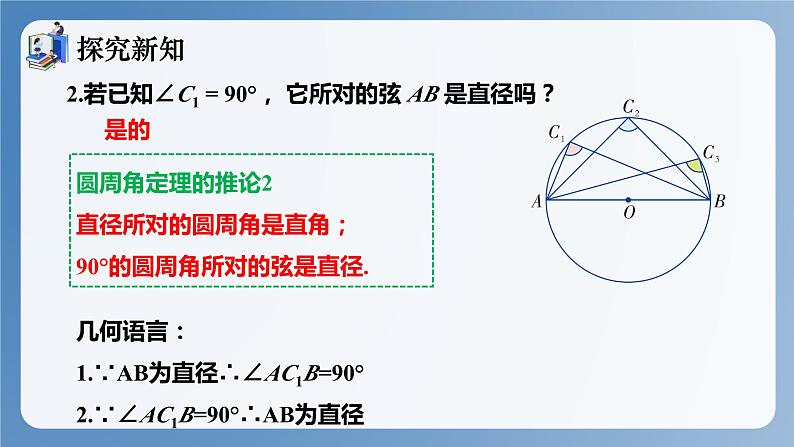
2.若已知∠C1 = 90°, 它所对的弦 AB 是直径吗?
圆周角定理的推论2直径所对的圆周角是直角; 90°的圆周角所对的弦是直径.
几何语言:1.∵AB为直径∴∠AC1B=90°2.∵∠AC1B=90°∴AB为直径
3.回归到最初的问题,你能确定圆形的圆心吗?
利用三角板在圆中画出两个 90° 的圆周角,这样就得到两条直径,那么这两条直径的交点就是圆心.
例1 如图,BC 是⊙O 的直径,∠ABC = 60°,点 D 在⊙O 上,求∠ADB 的度数.
解 ∵ BC为直径,∴ ∠BAC = 90°.又∠ABC = 60°,∴ ∠C = 30°.又∵ ∠ADB与∠C都是 所对的圆周角,∴ ∠ADB =∠C = 30°.
例2 如图,⊙O 的直径 AC 为 10 cm,弦 AD 为 6 cm.(1)求 DC 的长;
在 Rt△ABC 中,AB2+BC2 = AC2,
(2)∵ AC 是直径,∴ ∠ABC = 90°. ∵BD 平分 ∠ADC,∴∠ADB =∠CDB. 又∵∠ACB =∠ADB ,∠BAC =∠BDC . ∴ ∠BAC =∠ACB. ∴AB = BC.
(2)若∠ADC 的平分线交 ⊙O 于 B, 求 AB、BC 的长.
二 圆内接四边形的性质
如图,A,B,C,D 是圆 O 上的四点,顺次连接 A,B,C,D 四点,得到四边形 ABCD,我们把四边形 ABCD 称为圆内接四边形.
这个圆叫作这个四边形的外接圆.
在四边形 ABCD 中,两组对角∠A 与∠C,∠B 与∠D 有什么关系?
连接 OB,OD,∵ ∠A 所对的弧为 , ∠C 所对的弧为 ,又 与 所对的圆心角之和是周角,∴ ∠A + ∠C = = 180°
根据前面的探究,圆内接四边形的四个角之间有什么关系?
推论 圆内接四边形的对角互补.
几何语句:∵四边形ABCD为圆内接四边形,∴∠BAD+∠BCD =180°(圆内接四边形的对角互补).
例1 如图,四边形ABCD 为 ⊙O 的内接四边形,已知∠BOD 为 100°,求∠BAD 及∠BCD 的度数.
解 ∵ 圆心角∠BOD与圆周角∠BAD所对的弧为 ,∠BOD = 100°,∴ ∠BAD = ∠BOD = ×100°= 50°.∵ ∠BCD +∠BAD = 180°,∴ ∠BCD = 180°-∠BAD = 180°- 50°= 130°.
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有什么关系?
解:∠A=∠DCE.∵四边形ABCD是圆内接四边形,∴∠A+∠BCD=180°(圆内角四边形的对角互补).∵∠BCD+∠DCE=180°,∴∠A=∠DCE.
结论:圆内接四边形的外角等于它邻角的对角.
例2 如图,在⊙O中,AB 是直径,C,D 是圆上两点,且 AC = AD. 求证:BC = BD.
解 ∵ AC = AD, ∴ ∠ABC = ∠ABD .又∵ ∠C = ∠D = 90°, ∴∠CAB = ∠DAB ,∴ BC = BD.
∠C = ∠D = 90°
∠ABC = ∠ABD
例3 如图,圆内接四边形 ABCD 的外角 ∠DCE = 85°,求∠A 的度数.
解 ∵∠A +∠BCD = 180°,
∠BCD + ∠DCE = 180°,
∴∠A =∠DCE = 85°.
1.(2022山东济宁)如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan ∠CBD= ,则AD的长是________.
2. (分类讨论题)如图, A , B , C 是☉O 上的三点 , 且四 边形 OABC 是菱形.若点 D 是圆上异于 A , B , C 的 另一点 , 则∠ADC 的度数是____________.
∵AB为直径 ,∴∠BCA=90°(直径所对的圆周角为直角).∴∠BCD+∠DCA=90°.∵ ∠ACD=15°,∴∠BCD=90°-15°=75°.∴∠BAD=∠BCD=75°(同弧所对的圆周角相等).
3.如图,AB是⊙O的直径,∠C=15°,求∠BAD的度数.
∵∠ACD=15°, ∴∠AOD=2∠ACD =30°(圆周角的度数等于它所对弧上的圆心角的度数的一半).∵OA=OD,∴∠OAD=∠ODA.又∵∠AOD+∠OAD+∠ODA=180°,∴∠BAD=75°.
圆周角定理推论2及圆的内接四边形
直径所所对的圆周角是直角;90°的圆周角所对的弦是直径
圆内接四边形的对角互补.
1.教材P57第7~9题. 2.完成同步练习册中本课时的练习.
湘教版九年级下册2.2 圆心角、圆周角背景图ppt课件: 这是一份湘教版九年级下册2.2 圆心角、圆周角背景图ppt课件,共20页。
初中数学2.2 圆心角、圆周角图片课件ppt: 这是一份初中数学2.2 圆心角、圆周角图片课件ppt,共17页。
九年级下册2.2 圆心角、圆周角习题课件ppt: 这是一份九年级下册2.2 圆心角、圆周角习题课件ppt,共29页。














