数学必修 第二册15.3 互斥事件和独立事件集体备课ppt课件

这是一份数学必修 第二册15.3 互斥事件和独立事件集体备课ppt课件，共60页。PPT课件主要包含了第1课时互斥事件，互斥事件，AB＝∅，对立事件，AC＝∅且A＋C＝Ω，PA＋PB，规律方法，概率的加法公式，求对立事件的概率，课堂小结等内容，欢迎下载使用。
甲、乙两人下棋，甲不输的概率是0.6，两人下成平局的概率是0.3.问题：甲获胜的概率是多少？
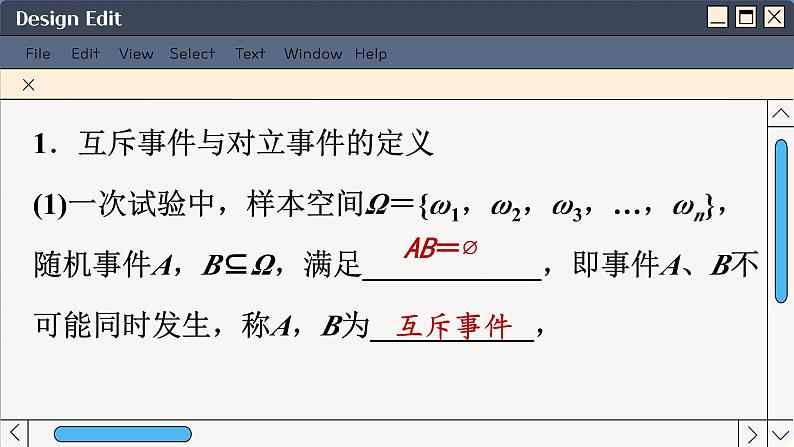
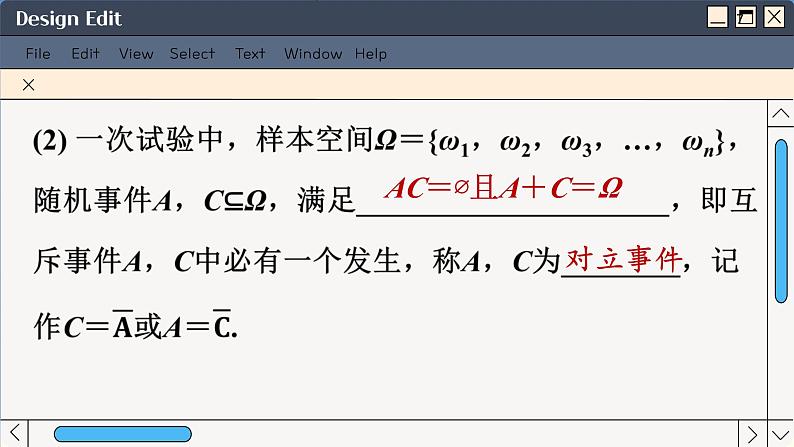
1．互斥事件与对立事件的定义(1)一次试验中，样本空间Ω＝{ω1，ω2，ω3，…，ωn}，随机事件A，B⊆Ω，满足____________，即事件A、B不可能同时发生，称A，B为___________，
如果事件A和事件B互斥，是指事件A和事件B在一次试验中不能同时发生，也就是说，事件A和事件B同时发生的交(和)概率为0，即P(AB)＝0.
思考：互斥事件与对立事件有什么区别和联系？提示：对立事件一定是互斥事件，互斥事件不一定是对立事件
2．概率加法公式(1)如果事件A，B互斥，那么事件A＋B发生的概率，等于事件A，B分别发生的概率的和，即P(A＋B)＝______________．这就是概率满足的第三个基本性质．
(2)一般地，如果事件A1，A2，…，An中任意两个事件都是互斥事件，那么事件A1，A2，…，An两两互斥．那么P(A1＋A2＋…＋An)＝_______________________，即彼此互斥事件和的概率等于每个事件概率的和．
P(A1)＋P(A2)＋…＋P(An)
1．给出以下结论：①互斥事件一定对立；②对立事件一定互斥；③互斥事件不一定对立；④事件A与B的和事件的概率一定大于事件A的概率；⑤事件A与B互斥，则有P(A)＝1－P(B)．其中正确的命题个数是(　　)A．2　　 B．3　　　　C．4　　　　D．5
对立必互斥，互斥不一定对立∴②③正确，①错又当A∪B＝A时，P(A∪B)＝P(A)，∴④错只有A与B为对立事件时，才有P(A)＝1－P(B)∴⑤错
2．甲、乙两人下棋，甲获胜的概率是40%，甲不输的概率为90%，则甲、乙两人下成和棋的概率为________．甲不输棋包含甲获胜或甲、乙两人下成和棋，则甲、乙两人下成和棋的概率为90%－40%＝50%
互斥事件与对立事件的判断
【例1】　某小组有3名男生和2名女生，从中任选2名同学参加演讲比赛．判断下列每对事件是不是互斥事件，如果是，再判断它们是不是对立事件．(1)“恰有1名男生”与“恰有2名男生”；(2)“至少有1名男生”与“全是男生”；
(1)“恰有1名男生”与“恰有2名男生”；因为“恰有1名男生”与“恰有2名男生”不可能同时发生，所以它们是互斥事件．当恰有2名女生时它们都不发生，所以它们不是对立事件．
(2)“至少有1名男生”与“全是男生”；因为恰有2名男生时“至少有1名男生”与“全是男生”同时发生，所以它们不是互斥事件．
(3)“至少有1名男生”与“全是女生”；因为“至少有1名男生”与“全是女生”不可能同时发生，所以它们是互斥事件．由于它们必有一个发生，所以它们是对立事件．
(4)“至少有1名男生”与“至少有1名女生”．当选出的是1名男生、1名女生时，“至少有1名男生”与“至少有1名女生”同时发生，所以它们不是互斥事件．
1．要判断两个事件是不是互斥事件，只需要分别找出各个事件包含的所有结果，看它们之间能不能同时发生．在互斥的前提下，看两个事件的并事件是否为必然事件，从而可判断是否为对立事件．
2．考虑事件的结果间是否有交事件，可考虑利用Venn图分析，对于较难判断的关系，也可考虑列出全部结果，再进行分析．
1．从40张扑克牌(红桃、黑桃、方块、梅花，点数从1～10各10张)中，任取一张．(1)“抽出红桃”与“抽出黑桃”；是互斥事件，不是对立事件．理由是：从40张扑克牌中任意抽取1张，“抽出红桃”和“抽出黑桃”是不可能同时发生的，所以是互斥事件．也不能保证其中必有一个发生，还可能抽出“方块”或者“梅花”，因此，二者不是对立事件．
(2)“抽出红色牌”与“抽出黑色牌”；既是互斥事件，又是对立事件．理由是：从40张扑克牌中，任意抽取1张，“抽出红色牌”与“抽出黑色牌”，两个事件不可能同时发生，但其中必有一个发生，所以它们既是互斥事件，又是对立事件．
(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”．判断上面给出的每对事件是否为互斥事件，是否为对立事件，并说明理由．不是互斥事件，当然不可能是对立事件．理由是：从40张扑克牌中任意抽取1张，“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生，如抽得牌点数为10，因此，二者不是互斥事件，当然不可能是对立事件．
2．某城市有甲、乙两种报纸供居民们订阅，记事件A：“只订甲报”，事件B：“至少订一种报”，事件C：“至多订一种报”，事件D：“不订甲报”，事件E：“一种报也不订”．判断下列每对事件是不是互斥事件，如果是，再判断它们是不是对立事件．(1)A与C；(2)B与E；(3)B与D；(4)B与C；(5)C与E.
(1)A与C由于事件C“至多订一种报”中有可能“只订甲报”，事件A与C有可能同时发生，故A与C不是互斥事件．(2)B与E事件B“至少订一种报”与事件E“一种报也不订”是不可能同时发生的，故B与E是互斥事件，又由于事件B与E必有一个发生，故B与E是对立事件．
(3)B与D事件B“至少订一种报”中有可能只订乙报，即有可能不订甲报，从而事件B与D有可能同时发生，故B与D不是互斥事件．
(4)B与C事件B“至少订一种报”中有这些可能：“只订甲报”“只订乙报”“订甲、乙两种报”．事件C“至多订一种报”中有这些可能：“一种报也不订”“只订甲报”“只订乙报”．由于这两个事件可能同时发生，故B与C不是互斥事件．
(5)C与E.由(4)知，事件E“一种报也不订”只是事件C的一种可能，故C与E有可能同时发生，故C与E不是互斥事件．
【例2】　某一时期内，一条河流某处的年最高水位在各个范围内的概率如下：
计算在同一时期内，河流此处的年最高水位在下列范围内的概率：(1)[10,18]；记此处河流的年最高水位在[8,10)，[10,12)，[12,14)，[14,16)，[16,18]范围内分别为事件A，B，C，D，E，则这5个事件是彼此互斥的，由互斥事件的概率加法公式
可得：此处河流的年最高水位在[10,18]的概率是P(B＋C＋D＋E)＝P(B)＋P(C)＋P(D)＋P(E)＝0.90.
(2)[8,14)．此处河流的年最高水位在[8,14)的概率是P(A＋B＋C)＝P(A)＋P(B)＋P(C)＝0.76.
1．将一个事件拆分为若干个互斥事件，分别求出各事件的概率，然后用加法公式计算结果．2．在运用互斥事件的概率加法公式解题时，首先要分清事件间是否互斥，同时要会把一个事件拆分成几个互斥事件，做到不重不漏．
3．常用步骤：(1)确定诸事件彼此互斥；(2)诸事件中有一个发生；(3)先求诸事件分别发生的概率，再求和．
4．某家庭电话在家中有人时，打进的电话响第1声时被接的概率为0.1，响第2声时被接的概率为0.3，响第3声时被接的概率为0.4，响第4声时被接的概率为0.1，那么电话在响前4声内被接的概率是多少？[解]　记“响第1声时被接”为事件A，“响第2声时被接”为事件B，“响第3声时被接”为事件C，“响第4声时被接”为事件D，“响前4声内被接”为事件E，
则易知A，B，C，D互斥，且E＝A＋B＋C＋D，所以由互斥事件的概率加法公式，得P(E)＝P(A＋B＋C＋D)＝P(A)＋P(B)＋P(C)＋P(D)＝0.1＋0.3＋0.4＋0.1＝0.9.
【例3】　一个袋中装有4个形状、大小完全相同的球，球的编号分别为1,2,3,4.(1)从袋中随机抽取2个球，求取出的球的编号之和不大于4的概率；
(2)先从袋中随机取1个球，该球的编号为m，将球放回袋中，再从袋中随机取1个球，该球的编号为n，求n