2023-2024学年河北省沧州市盐山县八年级（上）期末数学试卷（含解析）

这是一份2023-2024学年河北省沧州市盐山县八年级（上）期末数学试卷（含解析），共18页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

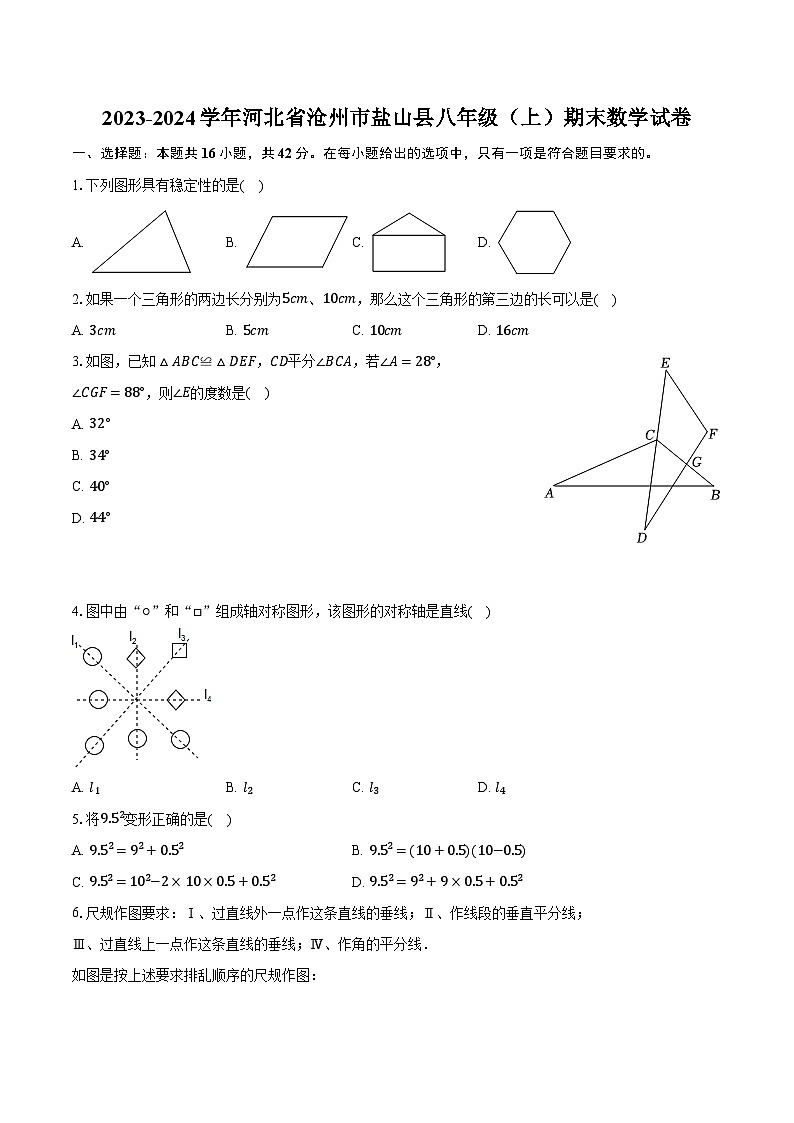
1.下列图形具有稳定性的是( )
A. B. C. D.
2.如果一个三角形的两边长分别为5cm、10cm，那么这个三角形的第三边的长可以是( )
A. 3cmB. 5cmC. 10cmD. 16cm
3.如图，已知△ABC≌△DEF，CD平分∠BCA，若∠A=28°，∠CGF=88°，则∠E的度数是( )
A. 32°
B. 34°
C. 40°
D. 44°
4.图中由“○”和“□”组成轴对称图形，该图形的对称轴是直线( )
A. l1B. l2C. l3D. l4
5.将9.52变形正确的是( )
A. 9.52=92+0.52B. 9.52=(10+0.5)(10−0.5)
C. 9.52=102−2×10×0.5+0.52D. 9.52=92+9×0.5+0.52
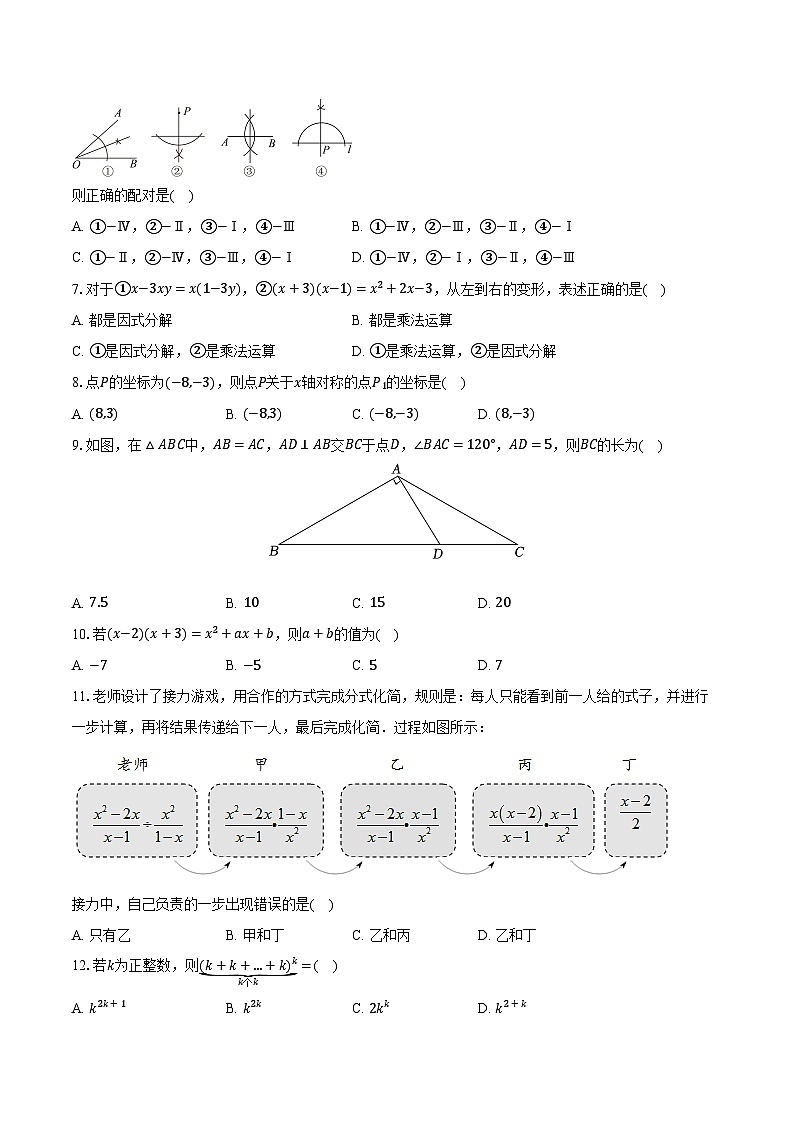
6.尺规作图要求：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；
Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．
如图是按上述要求排乱顺序的尺规作图：
则正确的配对是( )
A. ①−Ⅳ，②−Ⅱ，③−Ⅰ，④−ⅢB. ①−Ⅳ，②−Ⅲ，③−Ⅱ，④−Ⅰ
C. ①−Ⅱ，②−Ⅳ，③−Ⅲ，④−ⅠD. ①−Ⅳ，②−Ⅰ，③−Ⅱ，④−Ⅲ
7.对于①x−3xy=x(1−3y)，②(x+3)(x−1)=x2+2x−3，从左到右的变形，表述正确的是( )
A. 都是因式分解B. 都是乘法运算
C. ①是因式分解，②是乘法运算D. ①是乘法运算，②是因式分解
8.点P的坐标为(−8,−3)，则点P关于x轴对称的点P1的坐标是( )
A. (8,3)B. (−8,3)C. (−8,−3)D. (8,−3)
9.如图，在△ABC中，AB=AC，AD⊥AB交BC于点D，∠BAC=120°，AD=5，则BC的长为( )
A. 7.5B. 10C. 15D. 20
10.若(x−2)(x+3)=x2+ax+b，则a+b的值为( )
A. −7B. −5C. 5D. 7
11.老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简．过程如图所示：
接力中，自己负责的一步出现错误的是( )
A. 只有乙B. 甲和丁C. 乙和丙D. 乙和丁
12.若k为正整数，则k+k+...+kkk个k=( )
A. k2k+1B. k2kC. 2kkD. k2+k
13.一个正多边形每个内角与它相邻外角的度数比为2：1，则这个正多边形是( )
A. 正五方形B. 正六边形C. 正七边形D. 正八边形
14.若k为任意整数，则(2k+3)2−4k2的值总能( )
A. 被2整除B. 被3整除C. 被5整除D. 被7整除
15.科学家发现人体最小的细胞是淋巴细胞，直径约为0.0000061米，将数据0.0000061用科学记数法表示正确的是( )
A. 6.1×10−5B. 0.61×10−5C. 6.1×10−6D. 0.61×10−6
16.如图，若x为正整数，则表示(x+2)2x2+4x+4−1x+1的值的点落在
( )
A. 段①B. 段②C. 段③D. 段④
二、填空题：本题共3小题，共11分。
17.已知ax=−2，ay=3，则a3x−2y= ______．
18.(1)如图1，在△ABC中，BC=2，∠BAC>90°.AB的垂直平分线交BC于点E，AC的垂直平分线交BC于点F，则△AEF的周长为______．
(2)如图2，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，点E为AB的中点，连接DE，若AB=24，CD=6，则△DBE的面积为______．
19.现有甲、乙、丙三种不同的长方形纸片(边长如图)．
(1)取甲、乙纸片各1块，其面积和为 ；
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形，先取甲纸片1块，再取乙纸片4块，还需取丙纸片 块.
三、解答题：本题共7小题，共67分。解答应写出文字说明，证明过程或演算步骤。
20.(本小题8分)
(1)计算：(x+2)2+x(x−4)；
(2)因式分解：x3−6x2+9x．
21.(本小题9分)
解下列分式方程：
(1)2x−2=1+xx−2+1；
(2)2x+93x−9−4x−7x−3=2．
22.(本小题9分)
如图，△ABC和△CDE都为等边三角形，E在BC上，AE的延长线交BD于F．
(1)求证：AE=BD；
(2)求∠AFB的度数．
23.(本小题10分)
化简(xx+1+xx−1)⋅x2−1x.下面是甲、乙两同学的部分运算过程：
(1)甲同学解法的依据是______，乙同学解法的依据是______；(填序号)
①等式的基本性质；②分式的基本性质；③乘法分配律；④乘法交换律．
(2)按照甲乙两同学的解法，写出完整的解答过程．
24.(本小题10分)
某开发公司生产的960件新产品需要精加工后才能投放市场．现有甲、乙两个工厂都想加工这批产品，已知甲厂单独加工这批产品比乙工厂单独加工完这批产品多用20天，而甲工厂每天加工的数量是乙工厂每天加工数量的23，公司需付甲工厂加工费用每天80元，需付乙工厂加工费用每天120元．
(1)甲、乙两个工厂每天各能加工多少个新产品？
(2)公司制定产品加工方案如下：可以由每个厂家单独完成，也可以由两个厂家合作完成，在加工过程中，公司派一名工程师到厂进行技术指导，并负担每天10元的午餐补助费，请你帮助公司选择一种既省时又省钱的加工方案，并说明理由．
25.(本小题10分)
对于一个图形，通过不同的方法计算图形的面积，就可以得到一个数学等式．
(1)模拟练习，如图，写出一个我们熟悉的数学公式：______；
(2)解决问题：如果a+b=10，ab=16，求a2+b2的值；
(3)类比探究：如果一个长方形的长和宽分别为(8−x)和(x−2)，且(8−x)2+(x−2)2=22，求这个长方形的面积．
26.(本小题11分)
如图，在△ABC中，AB=AC，点D在边BC上(点D不与点B、点C重合)，作∠ADE
=∠B，DE交边AC于点E．
(1)求证：∠BAD=∠CDE；
(2)若DC=AB，求证：△ABD≌△DCE；
(3)当∠B=50°，且△ADE是等腰三角形时，直接写出∠BDA的度数．
答案和解析
1.【答案】A
【解析】解：具有稳定性的图形是三角形，
故选：A．
根据三角形具有稳定性判断即可．
本题考查的是三角形的性质，掌握三角形具有稳定性是解题的关键．
2.【答案】C
【解析】解：设第三边的长度为x cm，由题意得：
10−5即：5故选：C．
已知两边，则第三边的长度应是大于两边的差而小于两边的和，这样就可求出第三边长的范围，再选出答案即可．
此题主要考查了三角形的三边关系，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可．
3.【答案】A
【解析】解：∵△ABC≌△DEF，∠A=28°，
∴∠D=∠A=28°，∠B=∠E，
∴∠E+∠F=180°−∠D=180°−28°=152°，
在四边形ECGF中，∠ECG=360°−∠CGF−(∠E+∠F)=360°−88°−152°=120°，
∴∠DCB=180°−∠ECG=180°−120°=60°，
∵CD平分∠BCA，
∴∠BCA=2∠DCB=120°，
∴∠E=∠B=180°−∠A−∠BCA=180°−28°−120°=32°，
故选：A．
根据全等三角形的性质得出∠D=∠A=28°，∠B=∠E，根据三角形内角和定理求出∠E+∠F=152°，根据四边形的内角和定理求出∠ECG，求出∠BCD，根据角平分线的定义求出∠BCA=2∠DCB=120°，再根据三角形内角和定理求出答案即可．
本题考查了角平分线的定义，全等三角形的性质和三角形内角和定理，解题的关键是能熟记全等三角形的性质，注意：全等三角形的对应边相等，对应角相等．
4.【答案】C
【解析】解：该图形的对称轴是直线l3，
故选：C．
根据如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形，这条直线叫做对称轴进行分析即可．
此题主要考查了轴对称图形，关键是掌握轴对称图形的定义．
5.【答案】C
【解析】解：9.52
=(10−0.5)2
=102−2×10×0.5+0.52．
故选：C．
根据完全平方公式变形即可判断．
本题考查了完全平方公式，熟练掌握完全平方公式是解答本题的关键．
6.【答案】D
【解析】解：Ⅰ、过直线外一点作这条直线的垂线；Ⅱ、作线段的垂直平分线；
Ⅲ、过直线上一点作这条直线的垂线；Ⅳ、作角的平分线．
如图是按上述要求排乱顺序的尺规作图：
则正确的配对是：①−Ⅳ，②−Ⅰ，③−Ⅱ，④−Ⅲ．
故选：D．
分别利用过直线外一点作这条直线的垂线作法以及线段垂直平分线的作法和过直线上一点作这条直线的垂线、角平分线的作法分别得出符合题意的答案．
此题主要考查了基本作图，正确掌握基本作图方法是解题关键．
7.【答案】C
【解析】【分析】
本题考查了因式分解．解题的关键是掌握因式分解的定义：把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，根据定义即可解题．
【解答】
解：①x−3xy=x(1−3y)，从左到右的变形是因式分解；
②(x+3)(x−1)=x2+2x−3，从左到右的变形是整式的乘法，不是因式分解；
所以①是因式分解，②是乘法运算．
故选：C．
8.【答案】B
【解析】解：点P坐标是(−8,−3)，则点P关于x轴对称的点的坐标是(−8,3)，
故选：B．
根据关于x轴对称的点，横坐标相同，纵坐标互为相反数，可得答案．
本题考查了关于x轴对称的点的坐标，掌握好对称点的坐标规律：关于x轴对称的点，横坐标相同，纵坐标互为相反数；关于y轴对称的点，纵坐标相同，横坐标互为相反数是解决本题的关键．
9.【答案】C
【解析】解：∵AB=AC，∠BAC=120°，
∴∠B=∠C=12(180°−∠BAC)=30°，
∵AD⊥AB，
∴∠DAB=90°，
∴BD=2AD=10，∠CAD=∠BAC−∠BAD=30°，
∴∠C=∠CAD=30°，
∴CD=AD=5，
∴BC=BD+CD=10+5=15，
故选：C．
先利用等腰三角形的性质和三角形内角和定理可得∠B=∠C=30°，再根据垂直定义可得∠DAB=90°，从而在Rt△ABD中，利用含30度角的直角三角形的性质BD=2AD=10，然后利用角的和差关系求出∠CAD=30°，从而可得∠C=∠CAD=30°，再利用等角对等边可得CD=AD=5，最后进行计算即可解答．
本题考查了等腰三角形的判定与性质，含30度角的直角三角形，熟练掌握等腰三角形的判定与性质，以及含30度角的直角三角形的性质是解题的关键．
10.【答案】B
【解析】解：(x−2)(x+3)
=x2+3x−2x−6
=x2+x−6，
∵(x−2)(x+3)=x2+ax+b，
∴a=1，b=−6，
∴a+b=−5，
故选：B．
先根据多项式乘多项式法则展开，合并同类项，求出a、b值，再代入求出即可．
本题考查了多项式乘多项式法则，能正确根据多项式乘多项式法则展开是解此题的关键．
11.【答案】D
【解析】解：∵x2−2xx−1÷x21−x
=x2−2xx−1⋅1−xx2
=x2−2xx−1⋅−(x−1)x2
=x(x−2)x−1⋅−(x−1)x2
=−(x−2)x
=2−xx，
∴出现错误是在乙和丁，
故选：D．
根据分式的乘除运算步骤和运算法则逐一计算即可判断．
本题主要考查分式的乘除法，解题的关键是掌握分式乘除运算法则．
12.【答案】B
【解析】解：k+k+...+kkk个k
=(k×k)k
=(k2)k
=k2k．
故选：B．
根据幂的乘方的运算方法，判断出计算所求式的结果为多少即可．
此题主要考查了有理数的乘方和幂的乘方，要熟练掌握，解答此题的关键是要明确：(am)n=amn(m,n是正整数)．
13.【答案】B
【解析】解：∵一个正多边形每个内角与它相邻外角的度数比为2：1，
∴设这个外角是x，则内角是2x，
根据题意得x+2x=180°，
解得x=60°，
∴360°÷60°=6，
故选：B．
设这个外角是x°，则内角是2x°，根据内角与它相邻的外角互补列出方程求出外角的度数，根据多边形的外角和是360°即可求解．
本题考查了多边形的内角和外角，根据内角与它相邻的外角互补列出方程是解题的关键．
14.【答案】B
【解析】【分析】
先根据完全平方公式进行计算，再合并同类项，分解因式后再逐个判断即可．
本题考查了因式分解的应用，能求出(2k+3)2−4k2=3(4k+3)是解此题的关键．
【解答】
解：(2k+3)2−4k2
=4k2+12k+9−4k2
=12k+9
=3(4k+3)，
∵k为任意整数，
∴(2k+3)2−4k2的值总能被3整除，
故选：B．
15.【答案】C
【解析】解：0.0000061=6.1×10−6，
故选：C．
根据科学记数法的一般形式为a×10n，其中1≤|a|<10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正整数；当原数的绝对值小于1时，n是负整数．
本题考查科学记数法的表示方法．表示时关键要正确确定a的值以及n的值．
16.【答案】B
【解析】本题考查了分式的化简及分式加减运算，同时考查了分式值的估算，总体难度中等．
将所给分式的分母配方化简，再利用分式加减法化简，根据x为正整数，从所给图中可得正确答案．
解：(x+2)2x2+4x+4−1x+1=(x+2)2(x+2)2−1x+1=1−1x+1=xx+1．
∵xx+1=11+1x，且x为正整数，
∴0<1x≤1，1<1+1x≤2，
∴12≤11+1x<1，即12≤xx+1<1，
故表示(x+2)2x2+4x+4−1x+1的值的点落在段②．
故选：B．
17.【答案】−89
【解析】解：∵ax=−2，ay=3，
∴a3x−2y
=a3x÷a2y
=(ax)3÷(ay)2
=(−2)3÷32
=−8÷9
=−89，
故答案为：−89．
由a3x−2y根据同底数幂的乘法化成a3x÷a2y，再根据幂的乘方化成(ax)3÷(ay)2，代入求出即可．
本题考查了同底数幂的乘法，幂的乘方，有理数的混合运算，解题的关键是把原式化成(ax)3÷(ay)2，再进行计算．
18.【答案】2 36
【解析】解：(1)如图1，
∵AB的垂直平分线交BC于点E，AC的垂直平分线交BC于点F，
∴BE=AE，CF=AF，
∴△AEF的周长=AE+EF+CF=BE+EF+CF=BC=2．
故答案为：2．
(2)如图2，
过D作DH⊥AB于H，
∵∠C=90°，AD平分∠BAC，
∴DH=CD=6，
∵AB=24，
∴△ABD的面积=12AB⋅DH=12×24×6=72，
∵点E为AB的中点，
∴△DBE的面积=12×72=36．
故答案为：36．
(1)由线段垂直平分线的性质推出BE=AE，CF=AF，即可得到△AEF的周长=AE+EF+CF=BC=2．
(2)过D作DH⊥AB于H，由角平分线的性质推出DH=CD=6，求出△ABD的面积=12AB⋅DH=72，而点E为AB的中点，即可得到△DBE的面积=36．
本题考查线段垂直平分线的性质，角平分线的性质，关键是由线段垂直平分线的性质得到BE=AE，CF=AF，由角平分线的性质得到DH=CD．
19.【答案】a2+b2 ；
4.

【解析】【分析】
本题考查了完全平方式，掌握完全平方公式是解题的关键．
(1)由图可知：一块甲种纸片面积为a2，一块乙种纸片的面积为b2，一块丙种纸片面积为ab，即可求解；
(2)利用完全平方公式可求解．
【解答】
解：(1)由图可知：一块甲种纸片面积为a2，一块乙种纸片的面积为b2，
∴取甲、乙纸片各1块，其面积和为a2+b2，
故答案为：a2+b2；
(2)设取丙种纸片x块才能用它们拼成一个新的正方形，
∵一块甲种纸片面积为a2，一块乙种纸片的面积为b2，一块丙种纸片面积为ab，
∴a2+4b2+xab是一个完全平方式，
∴x=2×2=4，
故答案为：4．
20.【答案】解：(1)原式=x2+4x+4+x2−4x
=2x2+4；
(2)原式=x(x2−6x+9)
=x(x−3)2．
【解析】(1)先利用完全平方公式和单项式与多项式相乘的运算法则展开，再合并即可；
(2)先提取公因式，再利用完全平方式分解因式即可．
此题考查的是完全平方公式、单项式乘多项式、分解因式，应用完全平方公式时，要注意：①公式中的a，b可是单项式，也可以是多项式；②对形如两数和(或差)的平方的计算，都可以用这个公式；③对于三项的可以把其中的两项看作一项后，也可以用完全平方公式．
21.【答案】解：(1)2x−2=1+xx−2+1
方程两边同时乘以(x−2)，得
2=1+x+x−2，
解得：x=32；
当x=32时，x−2=32−2=−12≠0，
∴x=32是原方程的解；
(2)2x+93x−9−4x−7x−3=2，
方程两边同时乘以3(x−3)，得
2x+9−3(4x−7)=6(x−3)，
即2x+9−12x+21=6x−18，
解得：x=3，
当x=3时，3(x−3)=0，
∴原方程无解．
【解析】(1)方程两边同时乘以(x−2)，化为整式方程，解方程即可求解，最后要检验；
(2)方程两边同时乘以3(x−3)，化为整式方程，解方程即可求解，最后要检验．
本题考查了解分式方程，熟练掌握分式方程的解法是解题的关键．
22.【答案】(1)证明：∵△ABC和△CDE都为等边三角形，
∴∠ACB=∠BCD=60°，AC=BC，EC=DC，
在△ACE和△BCD中，
AC=BC∠ACB=∠BCDEC=DC，
∴△ACE≌△BCD(SAS)，
∴AE=BD，
(2)∵△ACE≌△BCD，
∴∠CAE=∠CBD，
∵∠CAB=∠CAE+∠EAB=∠CBD+∠EAB=60°，∠ABC=60°，
∴∠EAB+∠ABC+∠CBD=∠EAB+∠ABF=120°，
则∠AFB=60°
【解析】(1)由三角形ABC与三角形CDE都为等边三角形，利用等边三角形的性质得到两对边相等，夹角相等，利用SAS得到三角形ACE与三角形BCD全等，利用全等三角形对应边相等得到AE=CD．
(2)由全等三角形对应角相等得到∠CAE=∠CBD，再利用等边三角形的性质及三角形内角和定理即可求出∠AFB的度数．
此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．
23.【答案】② ③
【解析】解：(1)甲同学解法的依据是分式的基本性质，乙同学解法的依据是乘法分配律，
故答案为：②；③；
(2)若选择甲同学的解法：
(xx+1+xx−1)⋅x2−1x
=[x(x−1)(x+1)(x−1)+x(x+1)(x+1)(x−1)]⋅x2−1x
=x2−x+x2+x(x+1)(x−1)⋅(x+1)(x−1)x
=2x2(x+1)(x−1)⋅(x+1)(x−1)x
=2x；
若选择乙同学的解法：
(xx+1+xx−1)⋅x2−1x
=xx+1⋅x2−1x+xx−1⋅x2−1x
=xx+1⋅(x+1)(x−1)x+xx−1⋅(x+1)(x−1)x
=x−1+x+1
=2x．
(1)根据乘法分配律，以及分式的基本性质进行计算，即可解答；
(2)若选择甲同学的解法：先利用异分母分式加减法法则计算括号里，再算括号外，即可解答；若选择乙同学的解法：先利用乘法分配律计算分式的乘法，再算加减，即可解答．
本题考查了分式的混合运算，准确熟练地进行计算是解题的关键．
24.【答案】解：(1)设乙每天加工新产品x件，则甲每天加工新产品23x件．
根据题意得96023x−960x=20，
解得x=24，
经检验，x=24符合题意，则23x=24×23=16，
所以甲、乙两个工厂每天各能加工16个、24个新产品；
(2)甲单独加工完成需要960÷16=60天，费用为：60×(80+10)=5400元，
乙单独加工完成需要960÷24=40天，费用为：40×(120+10)=5200元；
甲、乙合作完成需要960÷(16+24)=24天，费用为：24×(120+80+10)=5040元．
所以既省时又省钱的加工方案是甲、乙合作．
【解析】(1)设乙每天加工新产品x件，则甲每天加工新产品23x件，甲单独加工完这批产品需96023x天，乙单独加工完这批产品需960x天，根据题意找出等量关系：甲厂单独加工这批产品所需天数−乙工厂单独加工完这批产品所需天数=20，由等量关系列出方程求解．
(2)分别计算出甲单独加工完成、乙单独加工完成、甲、乙合作完成需要的时间和费用，比较大小，选择既省时又省钱的加工方案即可．
本题主要考查分式方程的应用，解题的关键在于理解清楚题意，找出等量关系，列出方程求解．需要注意：①分式方程求解后，应注意检验其结果是否符合题意；②选择最优方案时，需将求各个方案所需时间和所需费用，经过比较后选择最优的那个方案．
25.【答案】(a+b)2=a2+b2+2ab．
【解析】解：(1)图中大正方形的面积可以表示为：(a+b)2，
还可以表示为：a2+b2+2ab．
∴(a+b)2=a2+b2+2ab．
故答案为：(a+b)2=a2+b2+2ab．
(2)∵(a+b)2=a2+b2+2ab．
∴a2+b2=(a+b)2−2ab=102−2×16=100−32=68．
(3)设a=8−x，b=x−2，
则a+b=6，a2+b2=22．
∵(a+b)2=a2+b2+2ab．
∴36=22+2ab．
∴ab=7．
∴这个长方形的面积为：(8−x)(x−2)=ab=7．
(1)用两种方法表示同一个图形面积即可．
(2)用(1)中得到的公式计算．
(3)将8−x，x−2当成两个字母后用公式．
本题考查完全平方公式的几何背景及其应用，用两种方法表示同一个图形面积，掌握完全平方公式的结构特征是求解本题的关键．
26.【答案】(1)证明：∠ADE=∠B，∠BAD+∠B=∠ADC，∠CDE+∠ADE=∠ADC，
∴∠BAD=∠CDE；
(2)证明：∵AB=AC，
∴∠B=∠C，
∵DC=AB，∠BAD=∠CDE；
在△ABD和△DCE中，
∠B=∠CAB=DC∠BAD=∠CDE，
∴△ABD≌△DCE(SAS)；
(3)解：∵∠B=∠C=50°，∠B+∠C+∠BAC=180°，
∴∠BAC=180°−∠B−∠C=180°−50°−50°=80°，
分三种情况讨论：
①当DA=DE时，∠DAE=∠DEA，
∵∠ADE=∠B=50°，∠ADE+∠DAE+∠DEA=180°，
∴∠DAE=(180°−50°)÷2=65°，
∴∠BAD=∠BAC−∠DAE=80°−65°=15°，
∵∠B+∠BAD+∠BDA=180°，
∴∠BDA=180°−∠B−∠BAD=180°−50°−15°=115°；
②当AD=AE时，∠AED=∠ADE=50°，
∵∠ADE+∠AED+∠DAE=180°，
∴∠DAE=180°−∠AED−∠ADE=180°−50°−50°=80°，
∵∠BAC=80°，
∴∠DAE=∠BAE，
∴点D与点B重合，不合题意．
③当EA=ED时，∠DAE=∠ADE=50°，
∴∠BAD=∠BAC−∠DAE=80°−50°=30°，
∵∠B+∠BAD+∠BDA=180°，
∴∠BDA=180°−∠B−∠BAD=180°−50°−30°=100°，
综上所述，当∠BDA的度数为115°或100°时，△ADE是等腰三角形．
【解析】(1)根据三角形的内角和定理即可得到结论；
(2)根据全等三角形的判定和性质定理即可得到结论；
(3)分三种情况讨论：①当DA=DE时，②当AD=AE时，③当EA=ED时，根据三角形的内角和定理以及等腰三角形的判定定理即可得到结论．
此题考查了全等三角形的判定与性质，平角的意义，三角形外角的性质，等腰三角形的性质，用分类讨论的思想解决问题是解本题的关键．解：原式=[x(x−1)(x+1)(x−1)+x(x+1)(x+1)(x−1)]⋅x2−1x
…
解：原式=xx+1⋅x2−1x+xx−1⋅x2−1x
…