

2023-2024学年湖北省黄冈市部分学校八年级(下)开学数学试卷
展开
这是一份2023-2024学年湖北省黄冈市部分学校八年级(下)开学数学试卷,共18页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
1.LOGO是标志、徽标或者商标的英文说法,是人们在长期的生活和实践中形成的一种视觉化的信息表达方式.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
2.已知△ABC的两边长为1和3,第三边的长为整数,则△ABC的周长是( )
A. 7B. 8C. 9D. 10
3.若分式x−3x+4有意义,则实数x的取值范围是( )
A. x=3B. x≠−4C. x≠3D. x=−4
4.一个多边形的内角和是它的外角和的6倍,则这个多边形是几边形?( )
A. 十一边形B. 十二边形C. 十三边形D. 十四边形
5.2023年上海微电子研发的28纳米浸没式光刻机的成功问世,标志着我国在光刻机领域迈出了坚实的一步.已知28纳米为0.000000028米,将数据0.000000028用科学记数法表示应为( )
A. 2.8×10−10B. 2.8×10−9C. 2.8×10−8D. 2.8×10−7
6.下列运算正确的是( )
A. x2+x2=x4B. 3a3⋅2a2=6a6
C. 2x4⋅(−3x4)=6x8D. (−a2)3=−a6
7.已知a−b=1,a2+b2=25,则ab的值为( )
A. 6B. 12C. 13D. 24
8.如图,在△ABC中,AC=BC,∠A=30°,CD⊥AC交AB于点D,CD=1,则AB的长是( )
A. 3B. 72C. 4D. 92
9.已知a,b,c为正整数,且满足2a×3b×4c=384,则a+b+c的取值不可能是( )
A. 5B. 6C. 7D. 8
10.如图,在△ABC,AB=AC,D为BC上的一点,∠BAD=20°,在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE,DE,DE交AC于点O,若CE//AB,则∠COE的度数为( )
A. 60°
B. 70°
C. 80°
D. 90°
二、填空题:本题共5小题,每小题3分,共15分。
11.计算:20240−2−1= ______.
12.已知点A关于x轴的对称点为B(m,3),关于y轴的对称点为C(2,n),那么m+n= ______.
13.如图,△ABC≌△DEC,点E在AB边上,∠ACD=50°,则∠DEC的度数为______.
14.因式分解:a2(x−y)+(y−x)= ______.
15.如图,△ABC中,∠B=40°,∠C=30°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE//AB,则∠ADE的度数为______.
三、计算题:本大题共1小题,共11分。
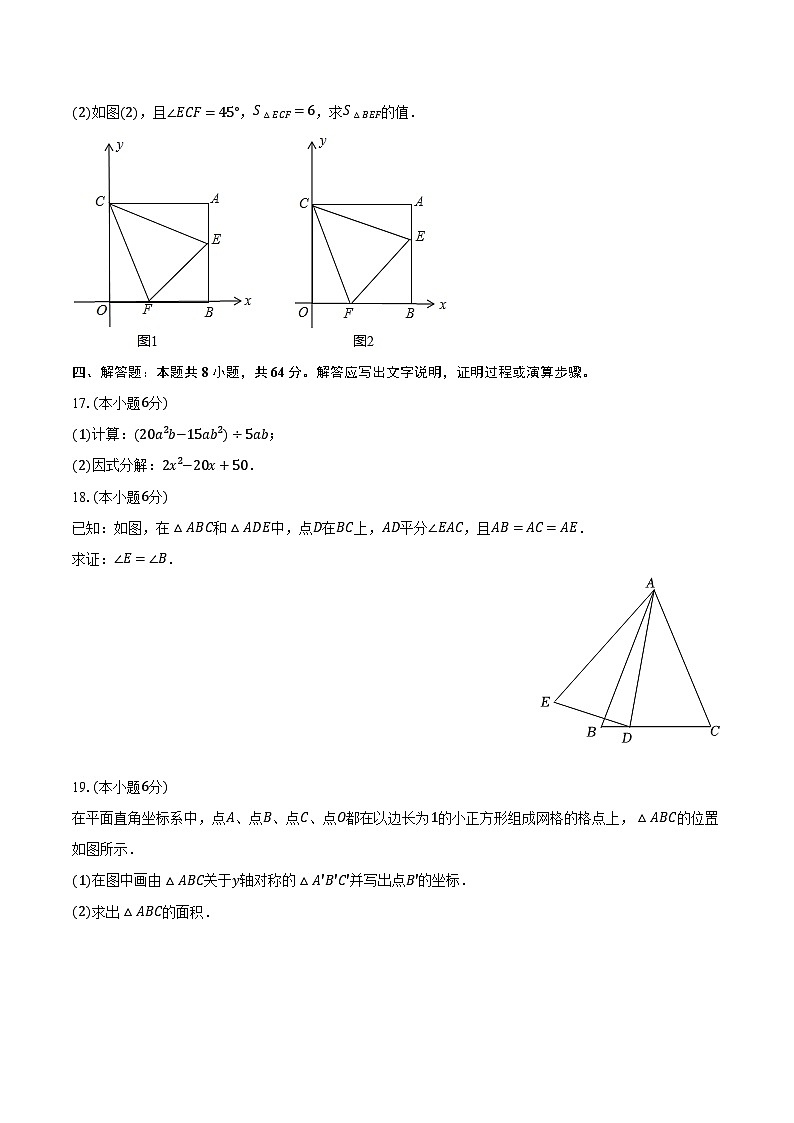
16.如图(1),在平面直角坐标系中,AB⊥x轴于B,AC⊥y轴于C,点C(0,4),A(4,4),过C点作∠ECF分别交线段AB、OB于E、F两点
(1)若OF+BE=AB,求证:CF=CE.
(2)如图(2),且∠ECF=45°,S△ECF=6,求S△BEF的值.
四、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
(1)计算:(20a2b−15ab2)÷5ab;
(2)因式分解:2x2−20x+50.
18.(本小题6分)
已知:如图,在△ABC和△ADE中,点D在BC上,AD平分∠EAC,且AB=AC=AE.
求证:∠E=∠B.
19.(本小题6分)
在平面直角坐标系中,点A、点B、点C、点O都在以边长为1的小正方形组成网格的格点上,△ABC的位置如图所示.
(1)在图中画由△ABC关于y轴对称的△A′B′C′并写出点B′的坐标.
(2)求出△ABC的面积.
20.(本小题7分)
先化简(2x2+2xx2−1−x2−xx2−2x+1)÷xx+1,再从−1,1,3中选择一个适当的数作头x的值代入求值.
21.(本小题8分)
已知:如图所示,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上匀速移动,它们的速度分别为VP=2cm/s,VQ=1.5cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为t s.
(1)当t为何值时,△PBQ为等边三角形?
(2)当t为何值时,△PBQ为直角三角形?
22.(本小题10分)
外出时佩戴口罩可以有效防控流感病毒,某药店用4000元购进若干包医用外科口罩,很快售完,该店又用7500元购进第二批同种口罩,第二批购进的包数比第一批多50%,每包口罩的进价比第一批每包的进价多0.5元,请解答下列问题:
(1)求购进的第一批医用口罩有多少包?
(2)政府采取措施,在这两批医用口罩的销售中,售价保持不变,若售完这两批口罩的总利润不高于3500元,那么药店销售该口罩每包的最高售价是多少元?
23.(本小题9分)
阅读下列材料:
因式分解的常用方法有提取公因式法和公式法,但有的多项式仅用上述方法就无法分解,如x2−2xy+y2−16.我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解.过程如下:x2−2xy+y2−16=(x−y)2−16=(x−y+4)(x−y−4).这种因式分解的方法叫分组分解法.利用这种分组的思想方法解决下列问题:
(1)因式分解:a2−6ab+9b2−36;
(2)△ABC三边a,b,c满足a2+c2+2b2−2ab−2bc=0,判断△ABC的形状并说明理由.
24.(本小题12分)
综合与探究小明在学习中遇到这样一个问题:如图1,∠MON=90°,点A,B分别在OM,ON上运动(不与点O重合).
探究与发现:若BC是∠ABN的平分线,BC的反向延长线与∠BAO的平分线交于点D.
(1)①若∠BAO=70°,则∠D= ______°;
②猜想:∠D的度数是否随A,B的运动而发生变化?并说明理由;
(2)拓展延伸:如图2,若∠ABC=13∠ABN,∠BAD=13∠BAO,求∠D的度数.
(3)在图1的基础上,如果∠MON=α,其余条件不变,随着点A、B的运动(如图3),∠D= ______(用含α的代数式表示)
答案和解析
1.【答案】D
【解析】解:A,B,C项中的图形都不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:D.
根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.【答案】A
【解析】解:∵△ABC的两边长为1和3,
∴第三边的取值范围是:2
相关试卷
这是一份湖北省黄冈市部分学校2023-2024学年八年级下学期开学考试数学试题,共10页。试卷主要包含了下列运算正确的是,已知,则的值为,如图,在中,,交于点,则的长是等内容,欢迎下载使用。
这是一份湖北省黄冈市部分学校2023-2024学年九年级下学期开学考试数学试题,共12页。试卷主要包含了若点,,在反比例函数等内容,欢迎下载使用。
这是一份湖北省黄冈市部分学校2022-2023学年八年级下学期期中数学试卷+,共17页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。









