人教A版 (2019)选择性必修 第二册4.3 等比数列第二课时教学设计

这是一份人教A版 (2019)选择性必修 第二册4.3 等比数列第二课时教学设计，共7页。
课题：等比数列的概念和通项公式的应用
课型：
课时教学目标
（1）能根据定义判断或证明用等差、等比数列构造的新数列的性质，发展逻辑推理素养.
（2）能在具体的问题情境中，发现数列的等比关系，抽象出等比数列模型，并能运用等比数列概念、通项公式、性质等解决实际问题，发展数学建模和运算求解素养.
教学重点和难点
（1）教学重点：等比数列的概念和通项公式的简单应用.
（2）教学难点：从具体情境中抽象出数列模型；对用等差、等比数列构造的数列的性质的探究.
教学资源和教学方法
教学过程
教学环节
师生活动
设计意图
教师个人二次备课
环节一
问题1 前面我们已经学习了等比数列的概念和通项公式等内容，你能说出等比数列的概念和通项公式吗？
师生活动 教师引导学生复习回顾等比数列的概念和通项公式，并请同学作答.
引导语 本节课我们将根据不同的问题情境，探讨等比数列的概念和通项公式的具体应用.
通过简单的复习回顾，巩固前面所学知识，为本课时的学习作好铺垫和引导.
环节二
例题练习，巩固应用
例4 用10000元购买某个理财产品一年.
（1）若以月利率0.400%的复利计息，12个月能获得多少利息（精确到1元）？
（2）若以季度复利计息，存4个季度，则当每季度利率为多少时，按季结算的利息不少于按月结算的利息（精确到10−5）？
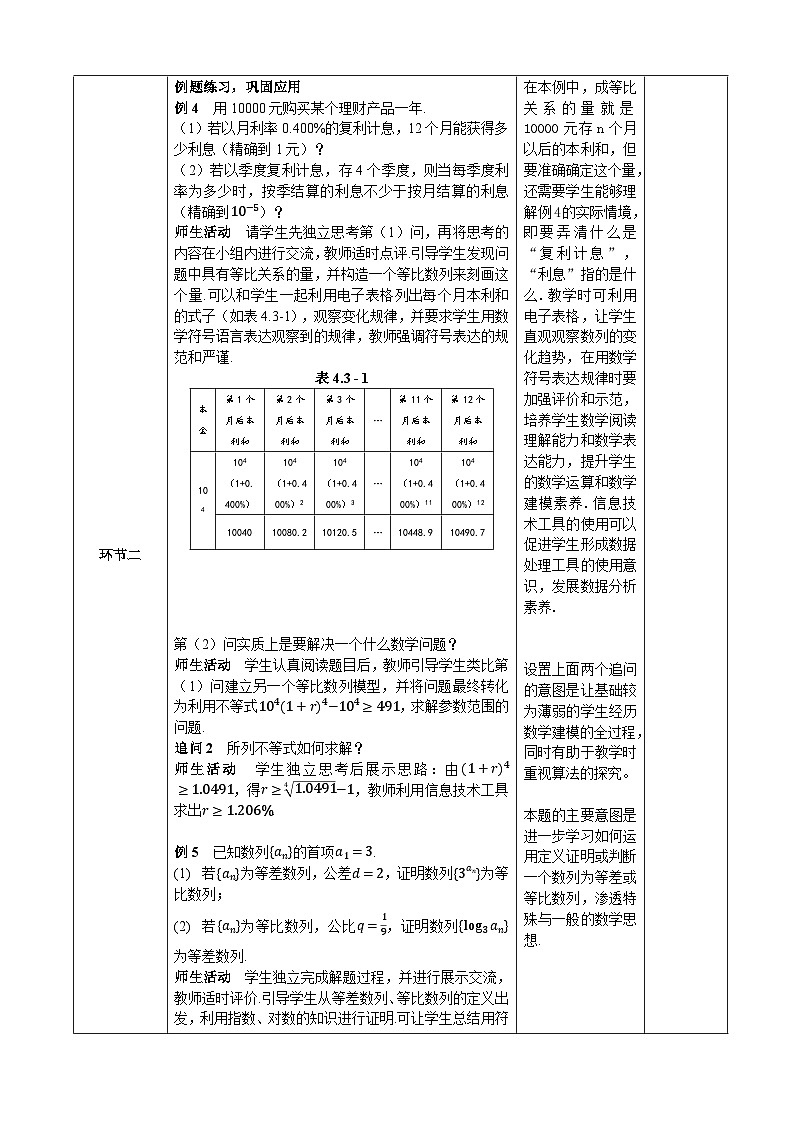
师生活动 请学生先独立思考第（1）问，再将思考的内容在小组内进行交流，教师适时点评.引导学生发现问题中具有等比关系的量，并构造一个等比数列来刻画这个量.可以和学生一起利用电子表格列出每个月本利和的式子（如表4.3-1），观察变化规律，并要求学生用数学符号语言表达观察到的规律，教师强调符号表达的规范和严谨.
表4.3 - 1
本金
第1个月后本利和
第2个月后本利和
第3个月后本利和
…
第11个月后本利和
第12个月后本利和
104
104（1+0.400%）
104（1+0.400%）2
104（1+0.400%）3
…
104（1+0.400%）11
104（1+0.400%）12
10040
10080.2
10120.5
…
10448.9
10490.7
第（2）问实质上是要解决一个什么数学问题？
师生活动 学生认真阅读题目后，教师引导学生类比第（1）问建立另一个等比数列模型，并将问题最终转化为利用不等式1041+r4−104≥491，求解参数范围的问题.
追问2 所列不等式如何求解？
师生活动 学生独立思考后展示思路：由1+r4≥1.0491，得r≥41.0491−1，教师利用信息技术工具求出r≥1.206%.
例5 已知数列{an}的首项a1=3.
若{an}为等差数列，公差d=2，证明数列{3an}为等比数列；
若{an}为等比数列，公比q=19，证明数列{lg3an}为等差数列.
师生活动 学生独立完成解题过程，并进行展示交流，教师适时评价.引导学生从等差数列、等比数列的定义出发，利用指数、对数的知识进行证明.可让学生总结用符号化定义证明等差数列、等比数列的基本路径，即利用所给条件证明第n+1项与第n项的差（比）为定值.比如第（1）问中，只需证明数列{3an}的第n+1项3an+1与第n项3an的比为定值即可.
变式 已知b>0且b≠1.
（1）如果数列{an}是等差数列，那么数列{ban}是否一定是等比数列？
（2）如果数列{an}是各项均为正的等比数列，那么数列{lgban}是否一定是等差数列？
师生活动 学生独立完成后进行展示，学生互评，教师强调符号表达的规范，并形成如下解答过程：
解 （1）设数列{an}的首项为a1，公差为d，则ban+1ban=ba1+ndba1+n−1d=bd，所以数列{ban}是以ba1为首项，bd为公比的等比数列.
（2）数列{an}是各项均为正的等比数列，设其首项为a1，公比为q，则lgban+1−lgban=lgban+1an=lgbq，所以数列{lgban}是以lgba1为首项，以lgbq为公差的等差数列.
追问1 知道了等差数列与等比数列之间的联系，我们能否把等差数列的一些性质迁移到等比数列中呢？例如，在等差数列{an}中，对于正整数p，q，s，t，若p+q=s+t，则ap+aq=as+at.那么，对于各项均为正数的等比数列{bn}，又有怎样的结论呢？
师生活动 启发学生根据变式（2）中的结论，利用{lgbn}为等差数列得到lgbn+lgbq=lgbs+lgbt，即lgbpbq=lgbsbt，于是相对应的结论是bpbq=bsbt.
追问2 上述结论如果去掉条件中的“各项均为正数”，是否仍然成立？即对于一般的等比数列{bn}都有这一结论吗？
师生活动 小组合作交流后，引导学生证明这个更为一般的结论.可将证明后的性质与等差数列的相关性质进行对比.
例6 某工厂去年12月试产1050个高新电子产品，产品合格率为90%.从今年1月开始，工厂在接下来的两年中将生产这款产品.1月按去年12月的产量和产品合格率生产，以后每月的产量都在前一个月的基础上提高5%，产品合格率比前一个月增加0.4%，那么生产该产品一年后，月不合格品的数量能否控制在100个以内？
师生活动 学生独立思考后小组合作交流，由学生展示建立数列模型的步骤：根据实际情境构建两个数列——等比数列{an}和等差数列{bn}，与问题的解决直接相关的量（各月不合格产品的数量）可以用这两个数列的乘积构成的数列{anbn}来表示.教师对学生数学语言的表达适时进行点评.
追问1 问题实际上是判断什么？请用数学式子予以表达.
师生活动 学生思考后回答：本题是判断当12