数学选择性必修 第二册4.2 等差数列第四课时教案设计

这是一份数学选择性必修 第二册4.2 等差数列第四课时教案设计，共7页。
课题：等差数列的应用
课型：
课时教学目标
（1）能解释等差数列的通项公式与前n项和公式的联系，说明等差数列前n项和公式与一元二次函数之间的共性与差异.
（2）在具体问题情境中，能正用、逆用和变用等差数列的前n项和公式，并解决相应的问题，进一步体会化归与转化的思想和基本量的方法.
教学重点和难点
（1）教学重点：等差数列前n项和公式的应用.
（2）教学难点：综合与灵活运用等差数列的前n项和公式.
教学资源和教学方法
教学过程
教学环节
师生活动
设计意图
教师个人二次备课
环节一
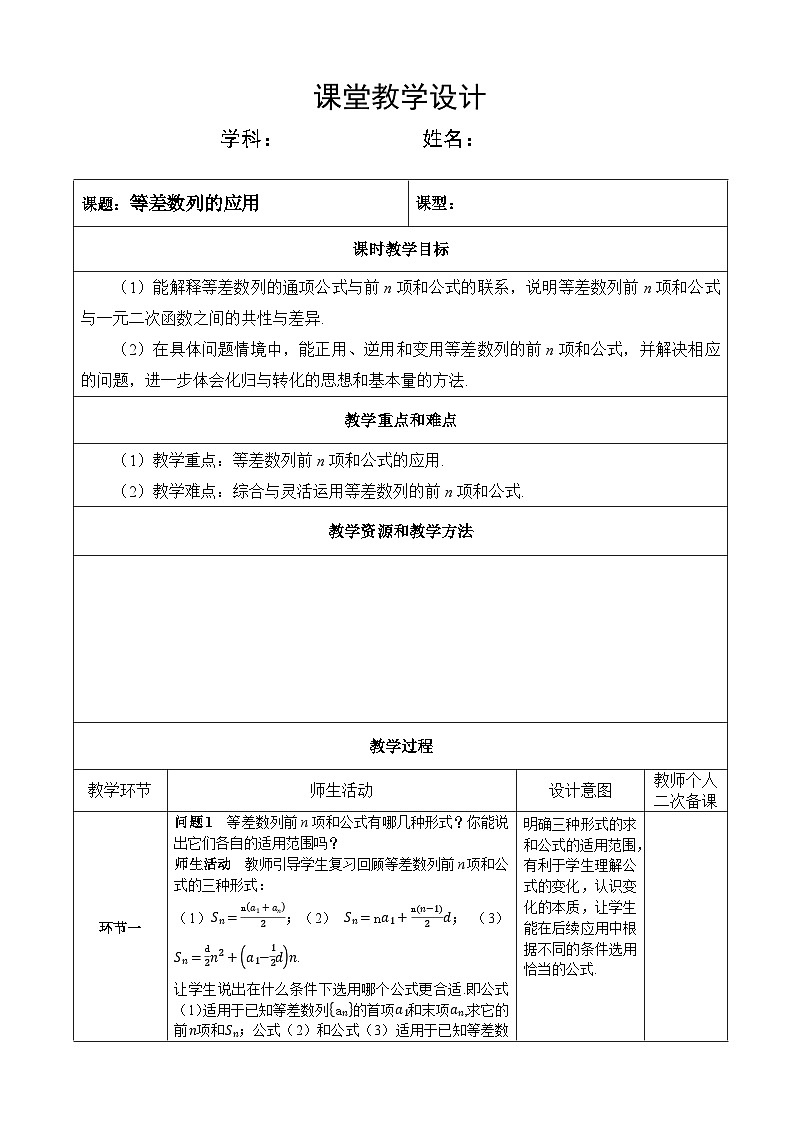
问题1 等差数列前n项和公式有哪几种形式？你能说出它们各自的适用范围吗？
师生活动 教师引导学生复习回顾等差数列前n项和公式的三种形式：
（1）Sn=na1+an2；（2） Sn=na1+nn−12d； （3） Sn=d2n2+a1−12dn.
让学生说出在什么条件下选用哪个公式更合适.即公式（1）适用于已知等差数列an的首项a1和末项an,求它的前n项和Sn；公式（2）和公式（3）适用于已知等差数列an的首项a1和公差d，求它的前n项和Sn·
明确三种形式的求和公式的适用范围，有利于学生理解公式的变化，认识变化的本质，让学生能在后续应用中根据不同的条件选用恰当的公式.
环节二
例题练习，巩固应用
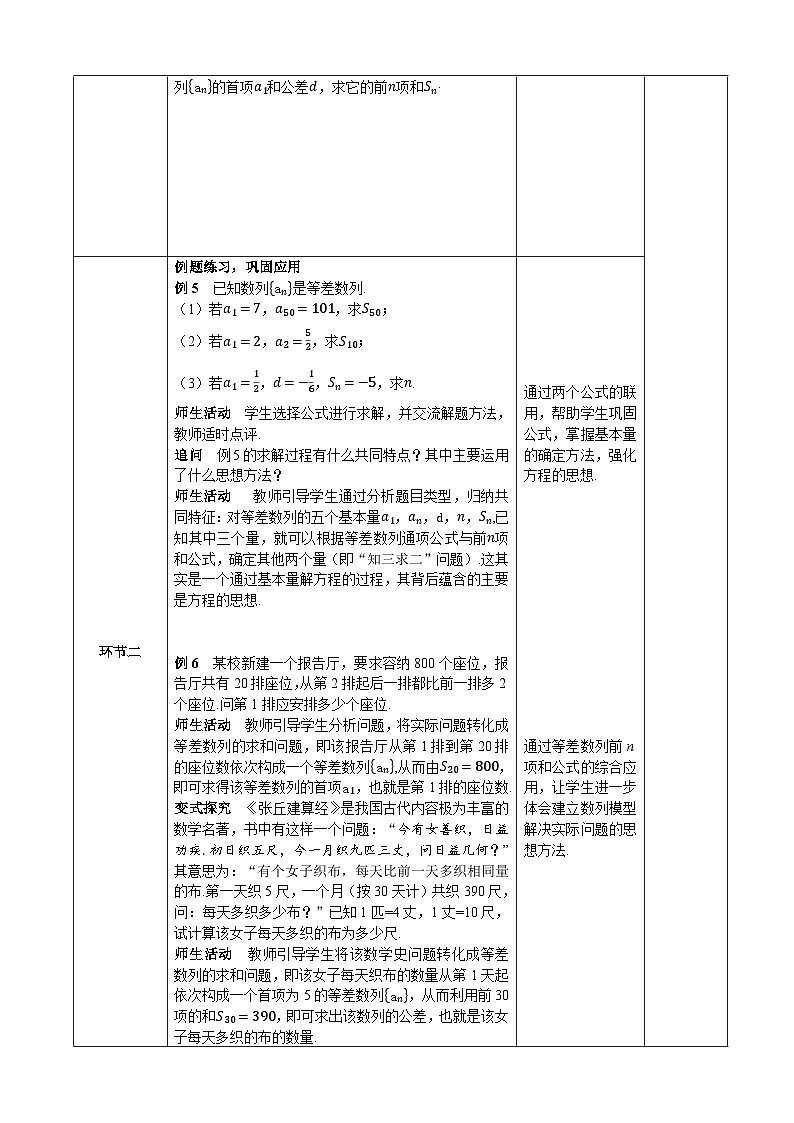
例5 已知数列an是等差数列.
（1）若a1=7，a50=101，求S50；
（2）若a1=2，a2=52，求S10；
（3）若a1=12，d=−16，Sn=−5，求n.
师生活动 学生选择公式进行求解，并交流解题方法，教师适时点评.
追问 例5的求解过程有什么共同特点？其中主要运用了什么思想方法？
师生活动 教师引导学生通过分析题目类型，归纳共同特征：对等差数列的五个基本量a1，an，d，n，Sn,已知其中三个量，就可以根据等差数列通项公式与前n项和公式，确定其他两个量（即“知三求二”问题）.这其实是一个通过基本量解方程的过程，其背后蕴含的主要是方程的思想.
例6 某校新建一个报告厅，要求容纳800个座位，报告厅共有20排座位，从第2排起后一排都比前一排多2个座位.问第1排应安排多少个座位.
师生活动 教师引导学生分析问题，将实际问题转化成等差数列的求和问题，即该报告厅从第1排到第20排的座位数依次构成一个等差数列an,从而由S20=800，即可求得该等差数列的首项a1，也就是第1排的座位数.
变式探究 《张丘建算经》是我国古代内容极为丰富的数学名著，书中有这样一个问题：“今有女善织，日益功疾.初日织五尺，今一月织九匹三丈，问日益几何？”其意思为：“有个女子织布，每天比前一天多织相同量的布.第一天织5尺，一个月（按30天计）共织390尺，问：每天多织多少布？”已知1匹=4丈，1丈=10尺，试计算该女子每天多织的布为多少尺.
师生活动 教师引导学生将该数学史问题转化成等差数列的求和问题，即该女子每天织布的数量从第1天起依次构成一个首项为5的等差数列an，从而利用前30项的和S30=390，即可求出该数列的公差，也就是该女子每天多织的布的数量.
追问 从例6及变式探究中，你能总结一下建立数列模型解决实际问题的基本步骤吗？
师生活动 教师引导学生归纳出建立数列模型的基本步骤：先将实际问题转化为数列问题，即用一个等差数列来表示实际问题中呈等差关系变化的量，再利用等差数列的通项公式和前n项和公式建立关于未知量的方程，通过解方程使问题获解.
例7 已知等差数列an的前n项和为Sn，若a1=10，公差d=−2，则Sn是否存在最大值？若存在，求Sn的最大值及取得最大值时n的值；若不存在，请说明理由.
师生活动 教师引导学生分析，学生独立选用两种方法解题，并进行展示交流.
追问 当d=−3.5时，Sn有最大值吗？你能利用函数思想，研究一下更一般的等差数列前n项和的最大（小）值问题吗？
师生活动 教师引导学生将两种解法拓展到一般情形，并归纳出如下结论：
（1） Sn是否有最大值，可利用公式（3），结合数列的图象得出结论.
（2）如果Sn有最大值，对应的项数n是一个还是两个值，关键要看数列an中是否有一项为0.若有，则使得Sn取得最大值的n有两个值；否则，n只有一个值.
利用同样的思想方法，可以研究当公差d>0时，等差数列前n项和Sn的最小值问题，
例8 已知一个等差数列an前10项的和是310，前20项的和是1220.由这些条件能确定这个等差数列的首项和公差吗？
师生活动 教师引导学生思考，将已知条件代入等差数列前n项和的公式（2）后，可得到两个关于a1与d的二元一次方程.解这两个二元一次方程所组成的方程组，就可以求得a1和d.学生独立完成解题过程，并进行展示交流.
追问 确定一个等差数列，需要几个相互独立的条件？如何根据等差数列给定项的和确定一个等差数列？
师生活动 教师提出问题后让学生讨论，并适时启发学生归纳结论：一般地，对于一个等差数列，只要给定两个独立条件，这个数列就完全确定.
变式1 设Sn是等差数列an的前n项和.
（1）若S10=50，S50=10，求S60的值；
（2）根据（1）中求得的结果，写出一个推广后的真命题，并给予证明
师生活动 学生独立思考、小组交流，再全班分享.对于第（1）问，引导学生从多种解题思路出发，如基本量方法、待定系数法、性质应用法等，灵活选用等差数列的前n项和公式的不同形式进行分析、求解和探究.对于第（2）问，让学生根据（1）的结果S60=−（50+10），经过合情推理得出如下一般性的推广结论：
设Sn是等差数列an的前n项和.若Sm=n，Sn=m，其中n≠m,则Sm+n=−m+n.
变式2 已知数列an的前n项和为Sn=pn2+qn+r，其中p，q，r为常数，且p≠0.任取若干组p，q，r，在电子表格中计算a1，a2，a3，a4，a5的值，观察数列an的特点，研究an是怎样的一个数列，试证明你的结论.
师生活动 教师让学生采用分组的方式动手操作实验.第一组选择r=0的情形.利用电子表格计算出a1=3，a2=5，a3=7, a4=9，a5=11.第二组选择r≠0的情形，利用电子表格类似计算出a1=4，a2=5，a3=7, a4=9，a5=11 （如图4.2 - 12所示）.
注：图4.2 - 12中的电子表格A栏中A1，A2，A3分别表示p，q，r的值，B栏表示an的序号n，C栏、D栏中分别是相应的Sn和an的值.
追问1 在上述实验操作过程中得到的数列分别是什么数列？
师生活动 教师应引导学生就不同的p，q，r的值对数表中的数据进行观察，形成猜想，得出结论：
（1）当r=0时，数列an是以2p为公差，p+q为首项的等差数列.
（2）当r≠0时，数列an从第二项起后续各项组成一个等差数列.
追问2 通过上述探究，你能得出更一般的结论吗？
师生活动 教师引导学生借助电子表格，通过分组实验，得到如下结论：
（1）一个数列是等差数列的充要条件是它的前n项和Sn是关于n的缺少常数项的二次式，即Sn=pn2+qn，且an=2pn+q−p.
（2）如果一个数列的前n项和Sn是关于n的含有常数项的二次式，即Sn=pn2+qn+r r≠0，那么这个数列从第二项起后续各项组成一个等差数列，且an=p+q+r， n=12pn+q−p， n≥2
通过两个公式的联用，帮助学生巩固公式，掌握基本量的确定方法，强化方程的思想.
通过等差数列前n项和公式的综合应用，让学生进一步体会建立数列模型解决实际问题的思想方法.
通过综合运用求和公式和函数的思想方法解决问题，探讨等差数列的单调性与其最值的关系，进一步强化等差数列的前n项和与一元二次函数的联系，提高学生对数列与函数的共性与差异的认识.
本例意在让学生进一步明确，首项和公差是确定一个等差数列的两个基本量，若将等差数列的前n项和视为一个新数列，则已知它的某两项，就能求出它的首项和公差，从而确定该等差数列.
该变式探究，既推广了等差数列前n项和的一个重要性质，又能让学生尝试一题多解、一题多变和引申推广，加深学生对等差数列前n项和公式的理解，提升学生灵活运用公式解决问题的能力.
让学生能从数的角度进一步认识等差数列前n项和公式的函数特征，加深对求和公式与通项公式的关系的理解；提供用信息技术研究数列问题的机会.
环节三
课堂练习，内化公式
教科书第24页练习第1、2、3、4题
师生活动 学生独立解答，教师引导学生交流，师生互动补充完善.
检验学生对等差数列的前n项和公式的掌握情况.
环节四
课堂小结，反思升华
问题2 回顾本单元的学习内容，回答下列问题：
（1）概述本单元知识发生发展过程的基本脉络
（2）等差数列前n项和公式的推导过程是怎样的？其中蕴含了哪些思想方法？
（3）我们是如何探讨等差数列前n项和公式的应用的？你能归纳一下问题的基本类型和解决问题的思想方法吗？
师生活动 学生独立思考并作适当交流，再让学生发言，教师引导完善，
强调“背景→方法探寻→求和公式→公式应用”的基本脉络，有助于学生掌握公式学习的基本路径，为后续等比数列前n项和公式的学习奠定基础；回顾“首尾配对法→分类讨论法→倒序相加法”的推导过程，帮助学生提炼出特殊与一般、分类与整合、化归与转化和数形结合等思想方法；培养学以致用的数学意识，领会解决问题的思想方法，积累运用公式的基本活动经验，落实数学运算和数学建模素养.
环节五
课堂检测，检验效果
1.设等差数列an的前n项和为Sn.若a1=2，S3=12,，则a6等于（ ）.
A.8 B.10 C.12 D.14
检测目标 本题主要检测学生对等差数列前n项和公式的理解程度，测评学生运用基本量的思想进行运算求解的能力.
2.设Sn是等差数列an的前n项和，若a1+a3+a5=3，则S5= .
检测目标 本题主要检测学生对等差数列前n项和公式的理解程度，测评学生运用等差数列的性质和整体运算策略解决问题的能力，
3.我国古代数学名著《九章算术》中有如下“竹九节”问题：现有一根9节的竹子，自上而下各节的容积成等差数列，且上面4节的容积共3升，下面3节的容积共4升，则九节竹的容积共有多少升？
检测目标 本题主要检测学生运用等差数列前n项和公式解决实际问题的能力.
师生活动 教师在学生独立完成后公布答案，并根据正确率适当讲评.第2题的解答方法灵活，可让学生充分展示不同思路，引导学生感悟一题多解与多解归一的辩证关系.
本组检测题主要评价学生对本单元核心知识、思想方法的综合应用能力，要求学生能综合应用等差数列的通项公式和求和公式解决相关问题.由于本组检测题的层次分明、方法灵活、综合性强，因而对学生来说有一定的挑战性.测评时应注重收集学生中存在的问题，加强点拨、注重启发，做到分类指导、分层教学，以促进学生的认知升华.
环节六
分层作业，应用迁移
1.基础性作业
（1）必做题：教科书第24~25页习题4.2第1、3、6、7、8题.
（2）选做题：教科书第24页练习第5题，第25页习题4.2第9题.
2.拓展性作业
设Sn为等差数列an的前n项和，已知S9=−a5.
（1）若a3=4，求an的通项公式；
（2）若a1>0，求使得Sn≥an时n的取值范围.
基础性作业主要考查学生对等差数列前n项和公式的理解程度，以及能否运用等差数列的性质解决问题.拓展性作业主要考查学生运用等差数列的通项公式和前n项和公式解决实际问题的能力.
作业设计
板书设计
教学反思