山东省烟台市牟平区2023-2024学年九年级上学期期末数学试题（含答案）

这是一份山东省烟台市牟平区2023-2024学年九年级上学期期末数学试题（含答案），共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

说明：解答全部在答题卡上完成，最后只交答题卡．
一、选择题：（本题共10个小题，每小题3分，满分30分．每小题都给出标号A、B、C、D的四个备选答案，其中只有一个是正确的，请将正确答案用2B铅笔在答题卡上涂黑．）
1．下列投影一定不会改变的形状和大小的是（ ）
A．中心投影B．平行投影
C．正投影D．当平行于投影面时的正投影
2．如图所示的立体图形是一个圆柱被截去四分之一后得到的几何体，它的左视图是（ ）
A．B．C．D．
3．利用课本上的科学计算器计算，下列按键顺序正确的是（ ）
A．
B．
C．
D．
4．小明和小凡玩“石头，剪刀，布”游戏，游戏规则：若两人出不同的手势，剪刀胜布；石头胜剪刀；布胜石头．若两人出相同的手势，则两人平局．下列命题中错误的是（ ）
A．小明不是胜就是负，所以小明胜的概率为
B．小明胜或小凡胜的概率相等
C．两人出相同手势的概率为
D．小凡胜的概率和两人出相同手势的概率一样
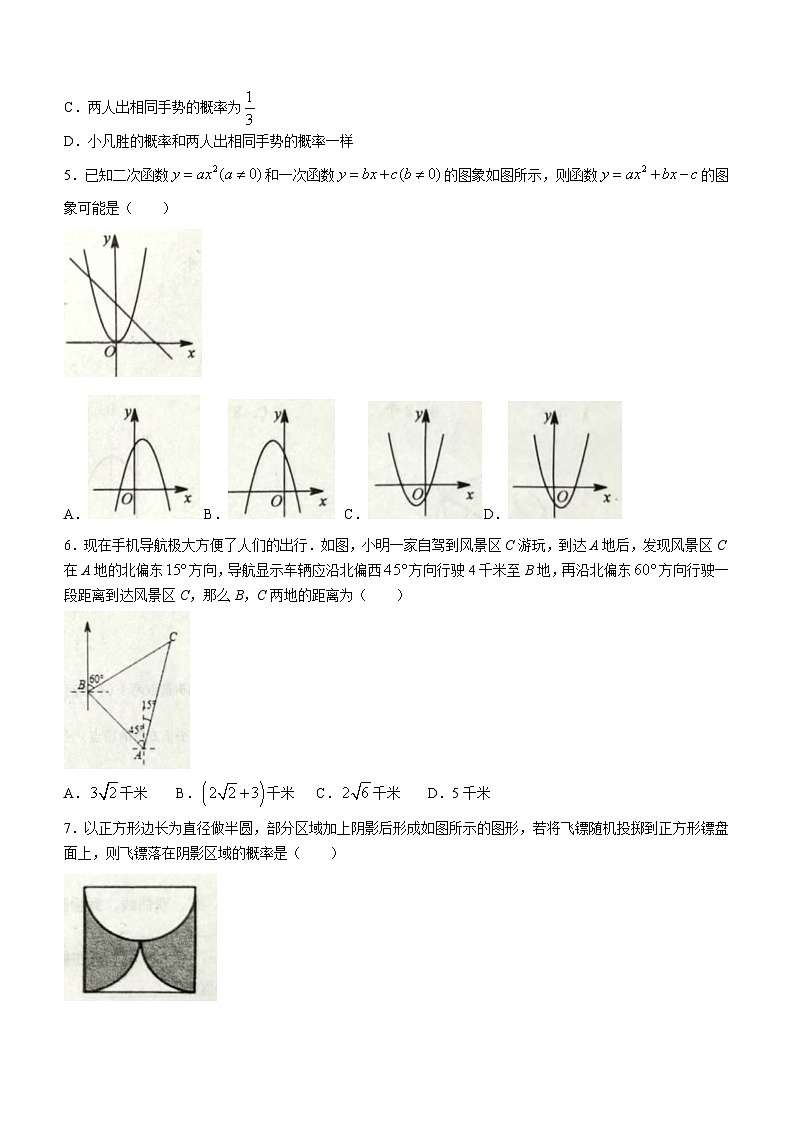
5．已知二次函数和一次函数的图象如图所示，则函数的图象可能是（ ）
A．B．C．D．
6．现在手机导航极大方便了人们的出行．如图，小明一家自驾到风景区C游玩，到达A地后，发现风景区C在A地的北偏东方向，导航显示车辆应沿北偏西方向行驶4千米至B地，再沿北偏东方向行驶一段距离到达风景区C，那么B，C两地的距离为（ ）
A．千米B．千米C．千米D．5千米
7．以正方形边长为直径做半圆，部分区域加上阴影后形成如图所示的图形，若将飞镖随机投掷到正方形镖盘面上，则飞镖落在阴影区域的概率是（ ）
A．B．C．D．
8．如图，在中，，，的面积为6，A0与x轴负半轴的夹角为，双曲线经过点A，则k的值为（ ）
A．B．C．D．
9．如图，是等边三角形ABC的外接圆，点D是劣弧AC上一动点（不与A，C重合），下列结论：①；②；③当DB最长时，；④，其中一定正确的结论有（ ）
A．1个B．2个C．3个D．4个
10．已知抛物线的对称轴是直线，其部分图象如图所示，下列说法中：①；②；③若、是抛物线上的两点，则有；④对于任意实数m，关于x的方程有两个不相等的实数根．以上说法正确的是（ ）
A．①②③B．②③④C．②④D．②③
二、填空题（每题3分，共18分）
11．从线段、等边三角形、平行四边形、圆、双曲线、抛物线中随机抽取两个（不放回），得到的图形都是中心对称图形的概率是__________．
12．如图，网格中小正方形的边长均为a，点A，B、C都在格点（小正方形的顶点）上，D是CA延长线上一点，则的值是__________．
13．如图，反比例函数在第一象限的图象与的两边AB、BC分别交于点、，已知轴，点A在y轴上，点C在x轴上，F为BC的中点，则的值为__________．
14．已知圆锥的三视图如图所示，则这个圆锥的侧面积为__________．
15．如图，的半径为4，圆心，点P是上的任一点，，且PA、PB与x轴分别交于A、B两点，若A、B两点关于原点O对称，则AB长的最小值为__________．
16．如图1，菱形ABCD的对角线AC与BD相交于点O，P、Q两点同时从O点出发，以1厘米/秒的速度在菱形的对角线及边上运动．点P的运动路线为，点Q的运动路线为．设运动的时间为x秒，P、Q间的距离为y厘米，y与x的函数关系的图象大致如图2所示，当点P在段上运动且P、Q两点间的距离最短时，P、Q两点的运动路程之和为__________厘米．
三、解答题（满分72分）
17．（本题6分）
某数学兴趣小组利用树影测量树高，如图①所示已测出树AB的影长AC为，并测出此时太阳光线与地面成夹角．（以下计算结果精确到，，，）
（1）求出树高AB；
（2）因水土流失，此时树AB沿太阳光线方向倒下，在倾倒过程中，树影长度发生了变化，假设太阳光线与地面夹角保持不变（用图②解答）：①求树与地面成角时的影长；②求树的最大影长．
18．（本题6分）
如图，一次函数的图象与x轴、y轴分别相交于C、B两点，与反比例函数在第一象限的图象相交于点．
（1）求反比例函数的表达式；
（2）点D在直线AB上且横坐标为4，过点D作y轴的平行线，交反比例函数的图象于点E，连接BE．求的面积．
19．（本题8分）
一个不透明的箱子里装有3个红色小球和若干个白色小球，每个小球除颜色外其他完全相同，每次把箱子里的小球㯰匀后随机摸出一个小球，记下颜色后再放回箱子里，通过大量重复实验后，发现摸到红色小球的频率稳定于0.75左右．
（1）请你估计箱子里白色小球的个数，并计算论证；
（2）现从该箱子里揁出1个小球，记下颜色后放回箱子里，摇匀后，再摸出1个小球，求两次摸出的小球颜色恰好不同的概率．（用画树状图或列表的方法）
20．（本题8分）
如图，四边形ABCD中，，，，连接BD，以点B为圆心，BA长为半径作，交BD于点E．
（1）试判断CD与的位置关系，并说明理由；
（2）若，，求图中阴影部分的面积．
21．（本题10分）
某通信公司欲在山上建设5G基站．如图，某处斜坡CB的坡比为1∶2.4，通讯塔AB垂直于水平地面，在C处测得塔顶A的仰角为，在D处测得塔顶A的仰角为斜坡路段CD长26米．
（1）求点D到水平地面CQ的距离；
（2）求通讯塔AB的高度．（参考数据：，，）
22．（本题10分）
超市购进某种葡萄，如果进价增加2元/千克要用300元；如果进价减少2元/千克，同样数量（千克）的葡萄只用200元．
（1）求葡萄的进价；
（2）如果购进这种葡萄不超过100千克，就按原价购进：如果购进葡萄超过100千克，超过部分购进价格减少2元/千克．写出购进葡萄的支出y（元）与购进数量x（千克）之间的函数关系式；
（3）超市一天购进葡萄数量不超过300千克，且购进葡萄当天全部销售完．据统计，销售单价z（元/千克）与一天销售数量x（千克）的关系为．在（2）的条件下，要使超市销售葡萄利润w（元）最大，求一天购进葡萄数量．（利润=销售收入-购进支出）
23．（本题10分）
如图，在中，，点D是AB边的中点，点O在AC边上，经过点C且与AB边相切于点E，．
（1）求证：AF是的切线；
（2）若，，求的半径及OD的长．
24．（本题14分）
如图，已知抛物线与x轴相交于A、B两点，与y轴相交于点C．其中，，，D是第一象限抛物线上一点，连接DC，交BC于点E，点D的横坐标为m．
（1）求抛物线的函数关系式；
（2）求线段DE长度的最大值；
（3）是否存在m的值，使是等腰三角形？若存在，请求出所有满足条件的m的值；若不存在，请说明理由．
2023—2024学年度第一学期期末质量检测
初四数学参考答案
一、选择题（每题3分，共30分）
二、填空题（每题3分，共18分）
11．12．113．1014．
15．1216．
三、解答题（本题共8个题，满分72分）
17．（本题6分）
解：（1）．
（2）①如图所示，过点作于点，
则；；
．
即树与地面成角时的影长约为．
②如图所示，当树与地面成角时影长最大，
最大为的长度（或树与光线垂直时影长最大），．
故树的最大影长约为．
18．（本题6分）
解：（1）将代得，点坐标为，
点A在反比例函数的图象上，，
反比例函数的表达式为；
（2）将代入一次函数得，即点D的坐标为，
将代入反比例函数得，即E点坐标为，
，．
19．（本题8分）
解：（1）通过多次摸球试验后发现，摸到红球的频率稳定在0.75左右，
估计摸到红球的概率为0.75，
设白球有x个，依题意得，解得，．
经检验：是原方程的解，且符合题意，
所以箱子里可能有1个白球；
（2）列表如下：
或画树状图如下：
一共有16种等可能的结果，两次摸出的小球颜色恰好不同的有：
、、、、、共6种．
两次摸出的小球恰好颜色不同的概率．
20．（本题8分）
解：（1）过点B作，，，
，，，
又，，，
，则点F在圆B上，与圆B相切；
（2），，是等边三角形，，
，，，
，，
阴影部分的面积．
21．（本题10分）
解：（1）过点D作，垂足为F，
斜坡CB的坡比为1∶2.4，，设，则，
在中，，，，解得：，（舍去），
，，
点D到水平地面CQ的距离为10米；
（2）延长AB交CQ于点E，过点D作，垂足为H，
由题意得：米，，
设，，，
在中，，，，
在中，，，，
，，，，
，，，
通讯塔AB的高度约为38.5米．
22．（本题10分）
解：（1）设葡萄的进价为x元/千克，由题意得：，解得：，
经检验：是方程的解，且符合题意，因此，葡萄的进价为10元/千克；
（2）当时，，
当时，，；
（3）若时，
当时，，
若时，，
当时，，
综上所述：当时，超市销售葡萄利润w最大．
因此，要使超市销售葡萄利润w最大，一天购进葡萄数量为200千克．
23．（本题10分）
（1）证明：如图，作，垂足为H，连接OE，
，D是AB的中点，，，
，又，
，即AC是的平分线，
在AC上，与AB相切于点E，，且OE是的半径，
平分，，是的半径．是的切线．
（2）解：如（1）图，在中，，，，
可设，，，，则，，
设的半径为r，则，
，．
，，即，则，
在中，，，由勾股定理得，又，，
在中，由勾股定理得：．
24．（本题14分）
解：（1），，，，
由题意，，，即，
，，，
由题意，解得，，，．
抛物线的函数关系式为．
（2）将和坐标分别代入得，解得，
线段BC所在直线的解析式为；
则，，
．
，当时，DE的最大值是4．
（3）存在
，，由勾股定理得，，作于点F，
则，，，，
，，
当时，，解得，，
当时，由题意，即，解得，
当时，，即，，
解得，．综上，满足条件的m的值为或4或3．
题号
1
2
3
4
5
6
7
8
9
10
答案
D
C
A
A
D
C
D
B
C
B
白
白