冀教版数学七年级下册 第六章 回顾与反思(3)课件

这是一份冀教版数学七年级下册 第六章 回顾与反思(3)课件，共22页。

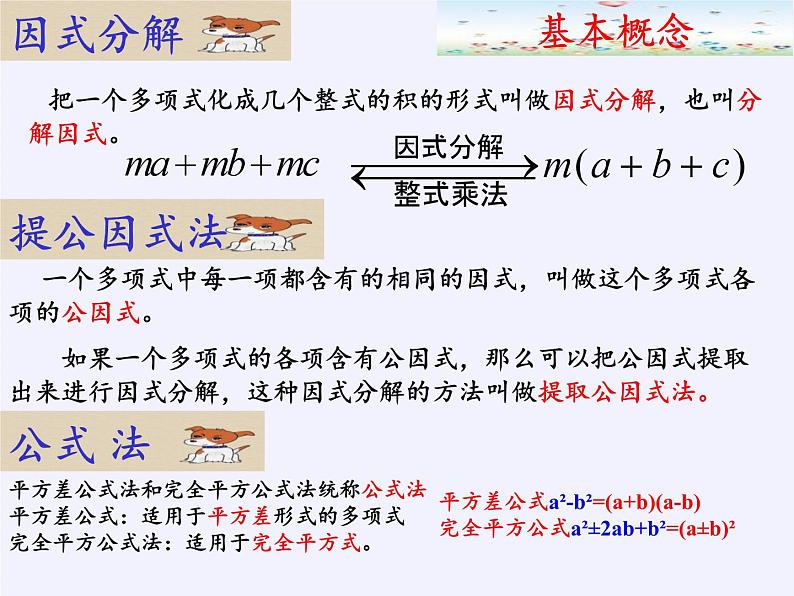
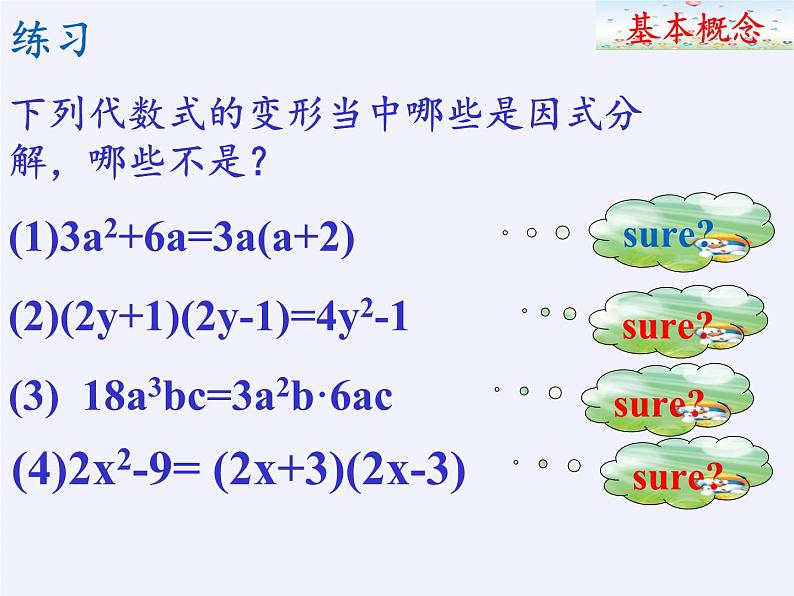
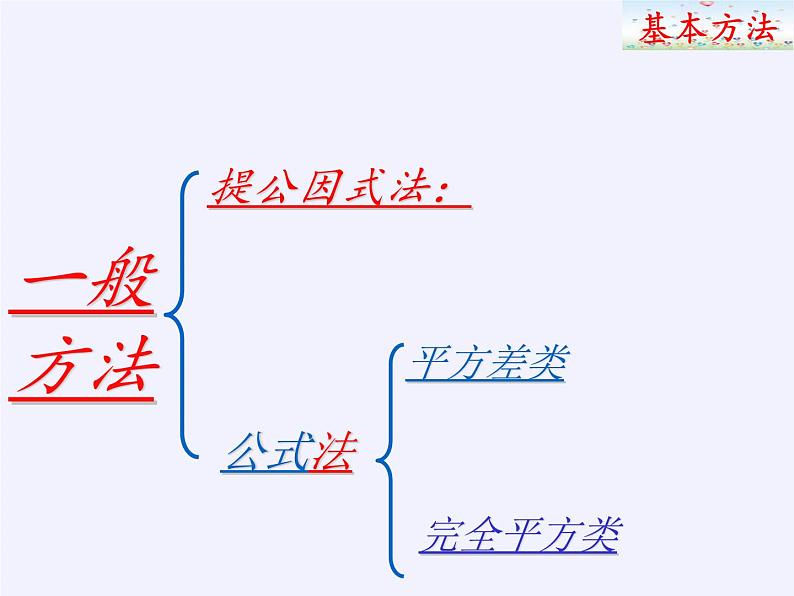
回顾与反思进一步理解因式分解的定义及因式分解与整式乘法的关系进一步理解公因式概念及找公因式的方法能灵活综合运用提公因式法，公式法分解因式学习目标平方差公式a²-b²=(a+b)(a-b)完全平方公式a²±2ab+b²=(a±b)² 把一个多项式化成几个整式的积的形式叫做因式分解，也叫分解因式。 一个多项式中每一项都含有的相同的因式，叫做这个多项式各项的公因式。 如果一个多项式的各项含有公因式，那么可以把公因式提取出来进行因式分解，这种因式分解的方法叫做提取公因式法。平方差公式法和完全平方公式法统称公式法平方差公式：适用于平方差形式的多项式完全平方公式法：适用于完全平方式。公式 法因式分解基本概念提公因式法否否是练习下列代数式的变形当中哪些是因式分解，哪些不是？(1)3a2+6a=3a(a+2)(2)(2y+1)(2y-1)=4y2-1(3) 18a3bc=3a2b·6ac sure?sure?sure?基本概念(4)2x2-9= (2x+3)(2x-3)否sure?一般方法提公因式法：公式法基本方法1.公因式确定（1）系数：取各系数的最大公约数；（2）字母：取各项相同的字母；（3）相同字母的指数：取最低指数。2.变形规律：（1）x-y=-(y-x) (2) -x-y=-(x+y) (3) (x-y)2=(y-x)2 (4) (x-y)3=-(y-x)33.一般步骤（1）确定应提取的公因式；（2）多项式除以公因式，所得的商作为另一个因式；（3）把多项式写成这两个因式的积的形式。提公因式法：用平方差公式分解因式的关键：多项式是否能看成两个数的平方的差；用完全平方公式分解因式的关键：在于判断一个多项式是否为一个完全平方式；平方差公式：a2-b2=(a+b)(a-b)完全平方公式：a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2 公式法挑战自我：A层练习 B层练习C层练习go!基本概念A层练习（抢答）将下列各式分解因式：⑴ -a²-ab； (2) x²+2xy+y²(3) 3am²-3an²； 基本方法=-a(a+b)=(x+y)²=3a (m+n)(m-n)B层练习将下列各式分解因式： ⑴ 18a²c-8b²c(2) x²y²-4xy+4(3) -b²+4a²C层练习(1) (2a+b)²–(a–b)² (2) (x+y)²-10(x+y)+25(3) 4a²–3b(4a–3b)基本方法=2c(3a+2b) (3a-2b)=（x y –2）²=(2a+b) (2a-b)=3a (a+2b)= (x+y-5)²= (2a- 3 b) ²探索与创新题 若9x2+kxy+36y2是完全平方式，则k= —∵9x2+kxy+36y2=(3x)2+kxy+(6y)2∴±kxy=2·3x·6y=36xy∴k=±36 做一做 1.若x2+(k+3)x+9是完全平方式，则k=___ k=3或k=-9 因式分解的一般步骤：一提：先看多项式各项有无公因式，如有公因式则要先提取公因式；二套：再看有几项， 如两项，则考虑用平方差公式；如三项，则考虑用完全平方公 式；四查：最后用整式乘法检验一遍，并看各因式能否再分解，如能分解，应分解到不能再分解为止。一般步骤三变：若以上两步都不行，则将考虑将多项式变形，使之能“提”或能“套”。[如(x+y)²-x-y=(x+y)(x+y-1）简化计算(1)562+56×44 (2)1012 – 992 (3)1012 +202×99+992 变式练习：32002 - 32001-32000能被5整除吗？为什么？求值A层练习B层练习1.如果|x-y-2|+(x+y+5)2=0,则x2-y2的值是( ) . -10 1.已知a、b为有理数,且a2+b2+2a+2b+2=0,试求a、b的值. C层练习a=-1, b=-13．几何应用已知：a,b,c是△ABC的三边长，且满足 ,试判断三角形的形状. 畅所欲言通过复习这节课你有哪些新的收获与感受?说出来与大家一起分享！1). 3m2-272). -x2+4x-4 3). (2x+y)2-(x+2y)2当堂检测4).计算： 20052-20042 =5）若a+b=3 , ab=2则a2b+ab2=6). 若x2-8x+m是完全平方式,则m=7). 若9x2+axy+4y2是完全平方式,则a=( )A. 6 B. 12 C. ±6 D. ±128.若x－y＝99求x2＋x＋y2－y－2xy之值 同学们， 你们最棒！请不要停止探究与创新的步伐，因为数学源自于对生活的热爱！谢 谢