- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.3 诱导公式及恒等变化(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.1 三角函数的性质(1)(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.2 三角函数的性质(2)(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.5 正余弦定理(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.5 正余弦定理(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
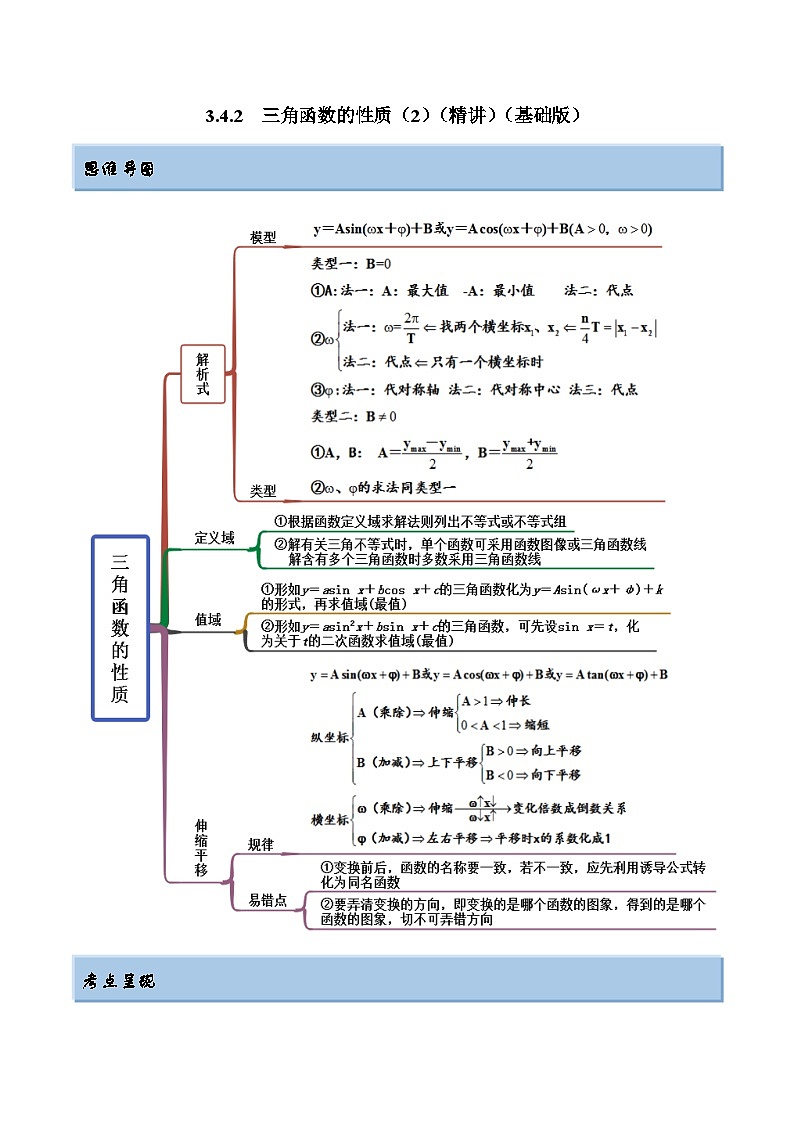
2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.2 三角函数的性质(2)(精讲)(基础版)(原卷版+解析版)
展开考点呈现
例题剖析
考点一 解析式
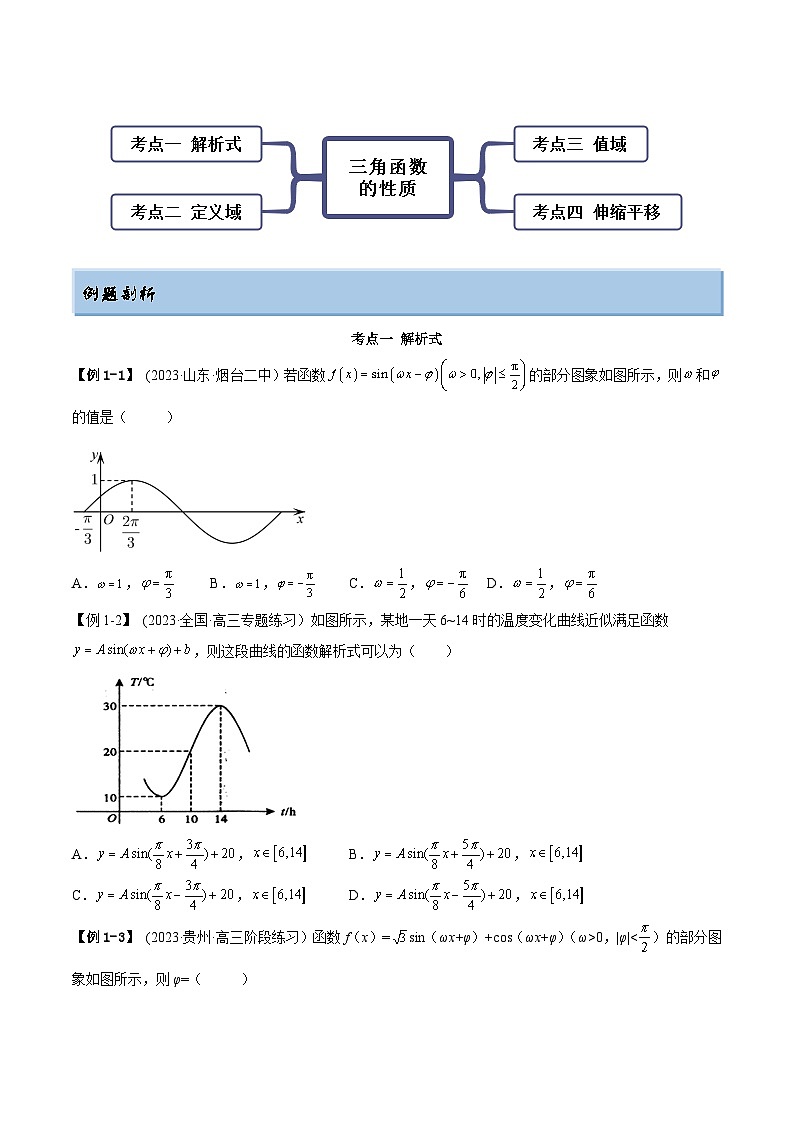
【例1-1】 (2023·山东·烟台二中)若函数的部分图象如图所示,则和的值是( )
A.,B.,C.,D.,
【例1-2】 (2023·全国·高三专题练习)如图所示,某地一天6~14时的温度变化曲线近似满足函数,则这段曲线的函数解析式可以为( )
A.,B.,
C.,D.,
【例1-3】 (2023·贵州·高三阶段练习)函数f(x)=sin(ωx+φ)+cs(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则φ=( )
A.B.-C.-D.
【一隅三反】
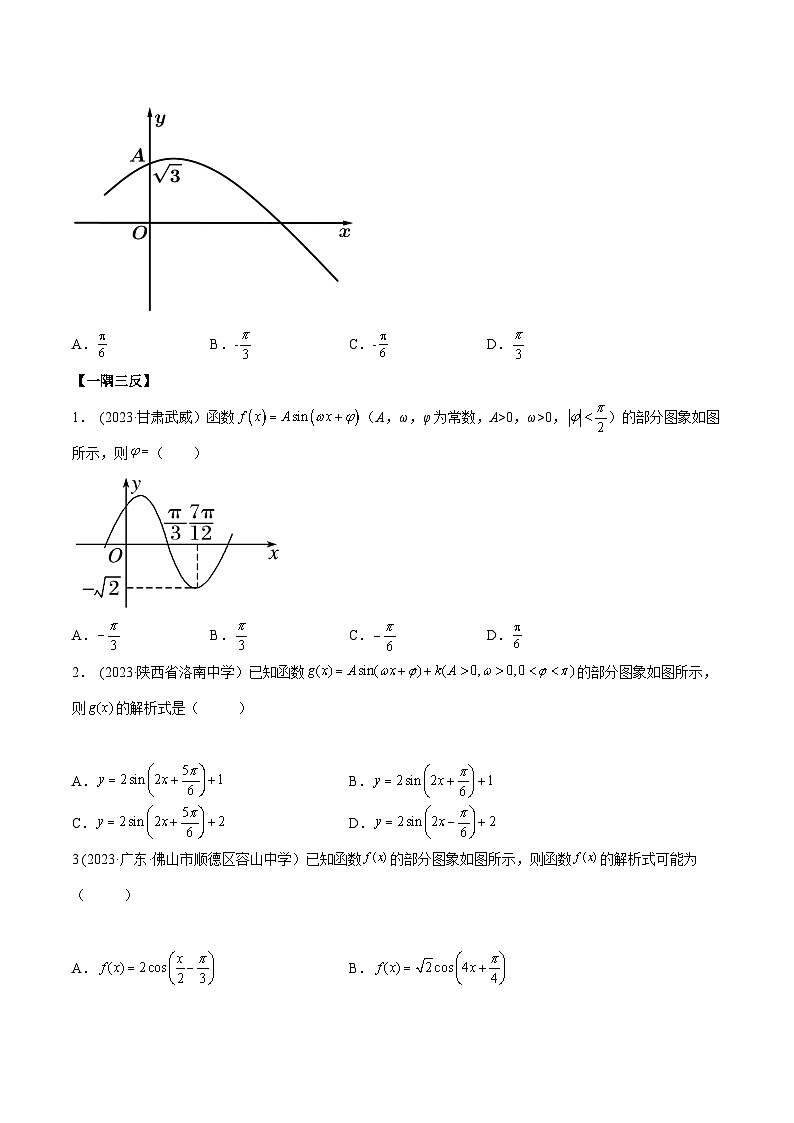
1. (2023·甘肃武威)函数(A,ω,φ为常数,A>0,ω>0,)的部分图象如图所示,则( )
A.B.C.D.
2. (2023·陕西省洛南中学)已知函数的部分图象如图所示,则的解析式是( )
A.B.
C.D.
3 (2023·广东·佛山市顺德区容山中学)已知函数的部分图象如图所示,则函数的解析式可能为( )
A.B.
C.D.
4. (2023·四川南充·二模)函数的部分图像如图所示,,则( )
A.关于点对称 B.关于直线对称
C.在上单调递减 D.在上是单调递增
考点二 定义域
【例2】 (2023·陕西·西安市临潼区铁路中学)求下列函数的定义域.
(1) (2) (3)
(1)整式函数的定义域为R;
(2)分式的分母不为零;
(3)偶次根式的被开方数不小于零;
(4)对数函数的真数必须大于零;
(5)正切函数y=tan x的定义域为;
(6)x0中x≠0;
(7)实际问题中除要考虑函数解析式有意义外,还应考虑实际问题本身的要求
温馨提示
【一隅三反】
1. (2023·全国·高三专题练习)若函数的定义域为( )
A.B.
C.D.
2.(2022·江苏)函数的定义域是( )
A.B.C.D.
3.(2022·四川绵阳)函数的定义域为
A.B.
C.D.
4. (2023·全国·高三专题练习)函数()的定义域是( )
A.B.C.D.
考点三 值域
【例3-1】 (2023·吉林)已知函数的最小正周期为,则函数在区间上的最大值与最小值的和是___________.
【例3-2】 (2023·全国·课时练习)已知,,则的最大值和最小值分别为______.
【例3-3】 (2023·宁夏·吴忠中学高三阶段练习(理))当时,不等式恒成立,则实数m的取值范围为____.
【一隅三反】
1 (2023·天津·高三期中)在区间的值域是_________.
2. (2023·北京二中)函数的值域为______.
3. (2023·全国·专题练习)已知函数.若关于的方程在上有解,则实数的取值范围是________.
4. (2023·四川·高三学业考试)已知函数.
(1)求函数的最小正周期;
(2)求函数在上的最值.
考点四 伸缩平移
【例4-1】 (2023·重庆市育才中学高三阶段练习)为了得到的图象,可将函数的图象( )
A.向左平移个单位B.向右平移个单位
C.向左平移个单位D.向右平移个单位
【例4-2】 (2023·河南省杞县高中模拟预测(理))已知函数的图象为C,为了得到函数的图象,只要把C上所有点( )
A.横坐标伸长到原来的2倍,纵坐标不变
B.横坐标缩短到原来的倍,纵坐标不变
C.纵坐标伸长到原来的2倍,横坐标不变
D.纵坐标缩短到原来的倍,横坐标不变
【例4-3】 (2023·陕西·二模)要得到函数的图象,只需将函数的图象( )
A.向左平移是个单位长度B.向左平移个单位长度
C.向右平移登个单位长度D.向右平移个单位长度
【例4-4】 (2023·山西·怀仁市第一中学校二模(理))将函数的图象上所有点的横坐标变为原来的一半、纵坐标不变,然后向右平移个单位长度后得到函数的图象,则( )
A.B.
C.D.
【例4-5】 (2023·四川达州·二模(理))将函数图象上所有点向左平移个单位长度,得到函数的图象,若是奇函数,则a的最小值是( )
A.B.C.D.
【一隅三反】
1. (2023·四川师范大学附属中学二模(文))函数其中,的图象如图所示,为了得到的图象只要将的图象( )
A.向右平移个单位B.向右平移个单位
C.向左平移个单位D.向左平移个单位
2. (2023·内蒙古包头·一模)把函数图象上所有点的横坐标伸长到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到函数的图象,则( )
A.B.C.D.
3. (2023·江西·南昌十中高三阶段练习)将函数的图象沿轴向左平移个单位后,得到关于轴对称的图象,则的最小值为( )
A.B.C.D.
4. (2023·陕西·模拟预测)把函数的图象向左平移个单位长度得到函数的图象,若在上是减函数,则实数a的最大值为( )
A.B.C.D.
3.4.2 三角函数的性质(2)(精讲)(基础版)
思维导图
考点呈现
例题剖析
考点一 解析式
【例1-1】 (2023·山东·烟台二中)若函数的部分图象如图所示,则和的值是( )
A.,B.,C.,D.,
【答案】C
【解析】由图象可知,所以,
,由于,所以.故选:C
【例1-2】 (2023·全国·高三专题练习)如图所示,某地一天6~14时的温度变化曲线近似满足函数,则这段曲线的函数解析式可以为( )
A.,B.,
C.,D.,
【答案】A
【解析】由于,所以,
又,所以,故,
又过点,则有,即,
所以,,取,得,符合题意选:A.
【例1-3】 (2023·贵州·高三阶段练习)函数f(x)=sin(ωx+φ)+cs(ωx+φ)(ω>0,|φ|<)的部分图象如图所示,则φ=( )
A.B.-C.-D.
【答案】A
【解析】因为,所以.
因为,所以,所以,即.故选:A
【一隅三反】
1. (2023·甘肃武威)函数(A,ω,φ为常数,A>0,ω>0,)的部分图象如图所示,则( )
A.B.C.D.
【答案】B
【解析】由图可知,,则,所以,所以,
将代入得,所以,
又,所以.故选:B.
2. (2023·陕西省洛南中学)已知函数的部分图象如图所示,则的解析式是( )
A.B.
C.D.
【答案】A
【解析】由图象可得,解得A=2,k=1,由正弦型图象性质可得,
所以,解得,又,且,所以,所以.故选:A
3 (2023·广东·佛山市顺德区容山中学)已知函数的部分图象如图所示,则函数的解析式可能为( )
A.B.
C.D.
【答案】A
【解析】设,由图可知,,,,则,
又,即,,
.故选:A.
4. (2023·四川南充·二模)函数的部分图像如图所示,,则( )
A.关于点对称 B.关于直线对称
C.在上单调递减 D.在上是单调递增
【答案】C
【解析】由图可知,且,所以,即,因为,所以,即,因为,所以函数关于直线对称,故A错误;
,所以函数关于对称,故B错误;
对于C:由,所以,因为在上单调递减,所以在上单调递减,故C正确;
对于D:由,则,因为在上不单调,所以在上不单调,故D错误;故选:C
考点二 定义域
【例2】 (2023·陕西·西安市临潼区铁路中学)求下列函数的定义域.
(1) (2) (3)
【答案】(1);(2);(3).
【解析】(1)要使得函数有意义,则,即,解得,
故函数定义域为.
(2)要使得函数有意义,则,即,解得,
故函数定义域为.
(3)要使得函数有意义,则,即,解得,故函数定义域为.
(1)整式函数的定义域为R;
(2)分式的分母不为零;
(3)偶次根式的被开方数不小于零;
(4)对数函数的真数必须大于零;
(5)正切函数y=tan x的定义域为;
(6)x0中x≠0;
(7)实际问题中除要考虑函数解析式有意义外,还应考虑实际问题本身的要求
温馨提示
【一隅三反】
1. (2023·全国·高三专题练习)若函数的定义域为( )
A.B.
C.D.
【答案】B
【解析】由题意,得,则.
故选:B.
2.(2022·江苏)函数的定义域是( )
A.B.C.D.
【答案】A
【解析】由题知, 由,解得
由解得,,
当时,由,解得.
当时,区间和无交集;
当时,区间和无交集;所以函数的定义域.故选:A.
3.(2022·四川绵阳)函数的定义域为
A.B.
C.D.
【答案】C
【解析】由函数,则满足,
令,解得
即函数的定义域为,故选C.
4. (2023·全国·高三专题练习)函数()的定义域是( )
A.B.C.D.
【答案】A
【解析】由题意,得,则,即,
∴.故选:A.
考点三 值域
【例3-1】 (2023·吉林)已知函数的最小正周期为,则函数在区间上的最大值与最小值的和是___________.
【答案】1或
【解析】由题设,,则,
在上,当则,故;当则,故;
综上,最大值与最小值的和为1或.故答案为:1或
【例3-2】 (2023·全国·课时练习)已知,,则的最大值和最小值分别为______.
【答案】,6
【解析】因,又函数在上单调递增,在上单调递减,于是得,
而,因此当时,,当或时,,所以的最大值和最小值分别为,6.故答案为:,6
【例3-3】 (2023·宁夏·吴忠中学高三阶段练习(理))当时,不等式恒成立,则实数m的取值范围为____.
【答案】
【解析】设,
则.
∵,∴,∴.
由题意知m
【一隅三反】
1 (2023·天津·高三期中)在区间的值域是_________.
【答案】
【解析】,
因为,所以,,所以,,所以函数的值域为,.
故答案为:,.
2. (2023·北京二中)函数的值域为______.
【答案】
【解析】依题意,原函数定义域为R,,而,
则当时,,当时,,所以所求值域是.故答案为:
3. (2023·全国·专题练习)已知函数.若关于的方程在上有解,则实数的取值范围是________.
【答案】
【解析】因为,
因为,所以,所以所以的值域为,
关于的方程在上有解,则关于的方程在上有解,所以,所以,所以实数的取值范围是故答案为:
4. (2023·四川·高三学业考试)已知函数.
(1)求函数的最小正周期;
(2)求函数在上的最值.
【答案】(1)(2)最大值为,最小值为
【解析】(1)∵,∴,即函数的最小正周期为.
(2)在区间上,,∴,
∴,∴的最大值为,的最小值为.
考点四 伸缩平移
【例4-1】 (2023·重庆市育才中学高三阶段练习)为了得到的图象,可将函数的图象( )
A.向左平移个单位B.向右平移个单位
C.向左平移个单位D.向右平移个单位
【答案】C
【解析】依题意,,
所以可由向左平移个单位得到.故选:C
【例4-2】 (2023·河南省杞县高中模拟预测(理))已知函数的图象为C,为了得到函数的图象,只要把C上所有点( )
A.横坐标伸长到原来的2倍,纵坐标不变
B.横坐标缩短到原来的倍,纵坐标不变
C.纵坐标伸长到原来的2倍,横坐标不变
D.纵坐标缩短到原来的倍,横坐标不变
【答案】B
【解析】根据三角函数的图象变换,将的图象上所有点的横坐标缩短为原来
倍,即可得到函数.故选:B.
【例4-3】 (2023·陕西·二模)要得到函数的图象,只需将函数的图象( )
A.向左平移是个单位长度B.向左平移个单位长度
C.向右平移登个单位长度D.向右平移个单位长度
【答案】B
【解析】因为函数,
,
所以要得到函数的图象,只需将函数的图象向左平移个单位长度.
故选:B.
【例4-4】 (2023·山西·怀仁市第一中学校二模(理))将函数的图象上所有点的横坐标变为原来的一半、纵坐标不变,然后向右平移个单位长度后得到函数的图象,则( )
A.B.
C.D.
【答案】B
【解析】将函数的图象上所有点的横坐标变为原来的一半、纵坐标不变,得到函数,再将函数向右平移个单位长度得到函数,所以.故选:B.
【例4-5】 (2023·四川达州·二模(理))将函数图象上所有点向左平移个单位长度,得到函数的图象,若是奇函数,则a的最小值是( )
A.B.C.D.
【答案】D
【解析】,则图象上所有点向左平移个单位长度,
得,因为是奇函数,所以,所以,因为,所以的最小值为,故选:D
【一隅三反】
1. (2023·四川师范大学附属中学二模(文))函数其中,的图象如图所示,为了得到的图象只要将的图象( )
A.向右平移个单位B.向右平移个单位
C.向左平移个单位D.向左平移个单位
【答案】A
【解析】由图可知,,得,所以,从而,
将代入可得,,因此,得,又,所以,所以,为了得到,所以将函数向右平移个单位即可.
故选:A.
2. (2023·内蒙古包头·一模)把函数图象上所有点的横坐标伸长到原来的倍,纵坐标不变,再把所得曲线向左平移个单位长度,得到函数的图象,则( )
A.B.C.D.
【答案】C
【解析】由题意可知,将函数的图象先向右平移个单位长度,得到函数的图象,
再将所得图象上所有点的横坐标缩短为原来的,纵坐标不变,可得到函数的图象.
故选:C.
3. (2023·江西·南昌十中高三阶段练习)将函数的图象沿轴向左平移个单位后,得到关于轴对称的图象,则的最小值为( )
A.B.C.D.
【答案】A
【解析】函数,
将函数的图象沿轴向左平移个单位后,得到函数,
因为函数是偶函数,.
当时,.则的最小值为故选:A
4. (2023·陕西·模拟预测)把函数的图象向左平移个单位长度得到函数的图象,若在上是减函数,则实数a的最大值为( )
A.B.C.D.
【答案】A
【解析】由题设,,则,
又上递减,即上递减,
由在上是减函数,则,故a的最大值为故选:A
2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.1 三角函数的性质(1)(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.1 三角函数的性质(1)(精讲)(基础版)(原卷版+解析版),共19页。试卷主要包含了周期,对称性,奇偶性等内容,欢迎下载使用。
备战2024年高考数学一轮复习(一隅三反基础版新高考专用)8-2 解析式(精讲)(基础版)(原卷版): 这是一份备战2024年高考数学一轮复习(一隅三反基础版新高考专用)8-2 解析式(精讲)(基础版)(原卷版),共4页。试卷主要包含了待定系数法求解析式,换元法求解析式,解方程组求解析式,配凑法等内容,欢迎下载使用。
备战2024年高考数学一轮复习(一隅三反基础版新高考专用)3-4-2 三角函数的性质(2)(精讲)(基础版)(原卷版): 这是一份备战2024年高考数学一轮复习(一隅三反基础版新高考专用)3-4-2 三角函数的性质(2)(精讲)(基础版)(原卷版),共8页。试卷主要包含了解析式,定义域,值域,伸缩平移等内容,欢迎下载使用。












