2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.2 三角函数的性质（2）（精练）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.4.2 三角函数的性质（2）（精练）（基础版）（原卷版+解析版），共31页。

A．B．C．D．
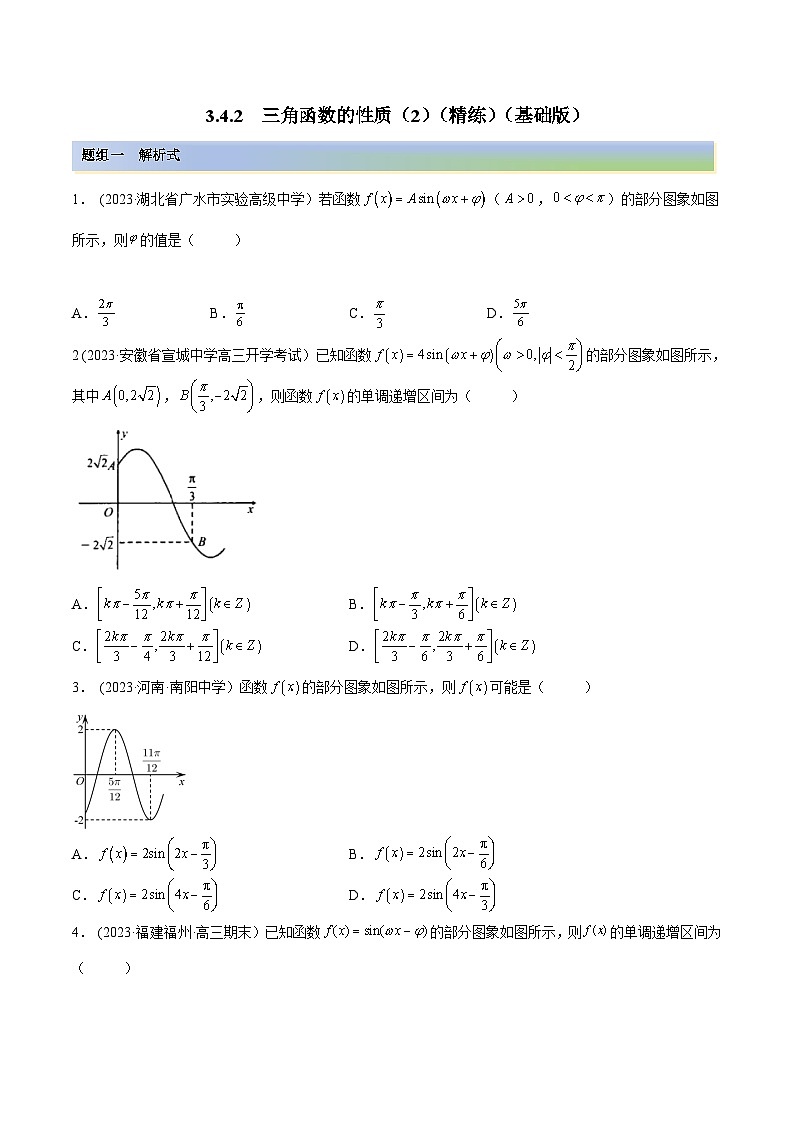
2 (2023·安徽省宣城中学高三开学考试）已知函数的部分图象如图所示，其中，，则函数的单调递增区间为（ ）
A．B．
C．D．
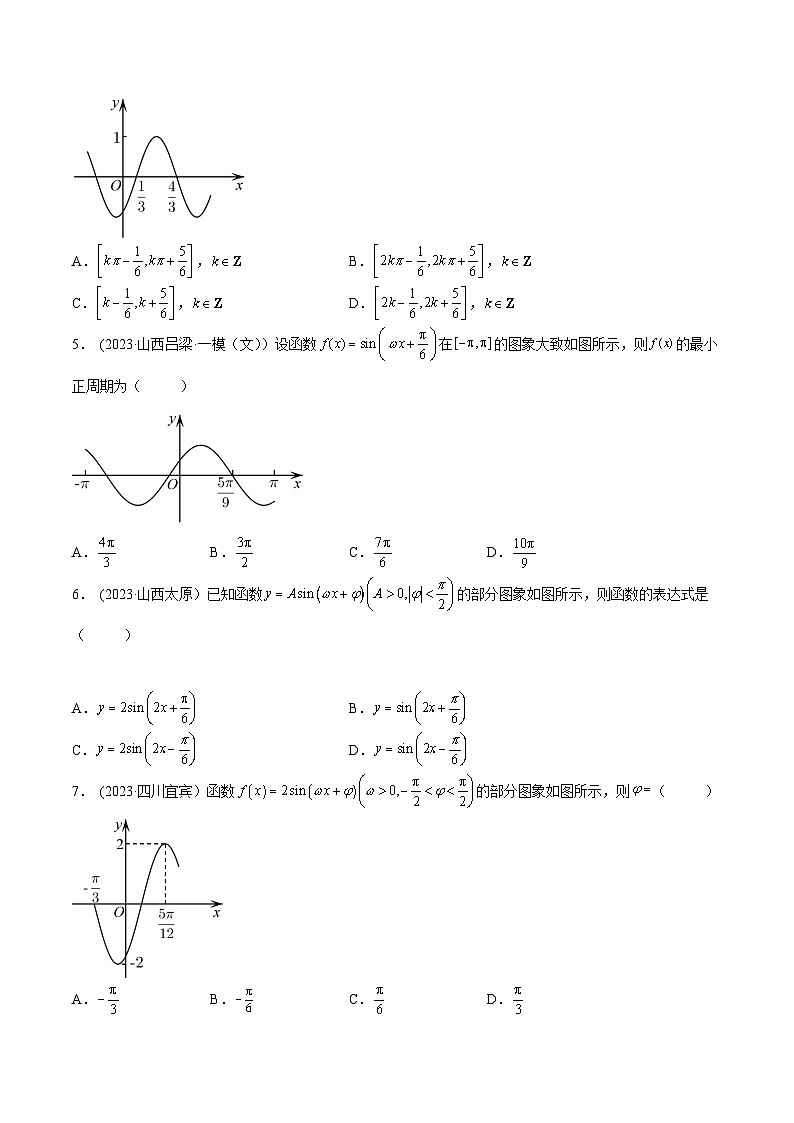
3． (2023·河南·南阳中学）函数的部分图象如图所示，则可能是（ ）
A．B．
C．D．
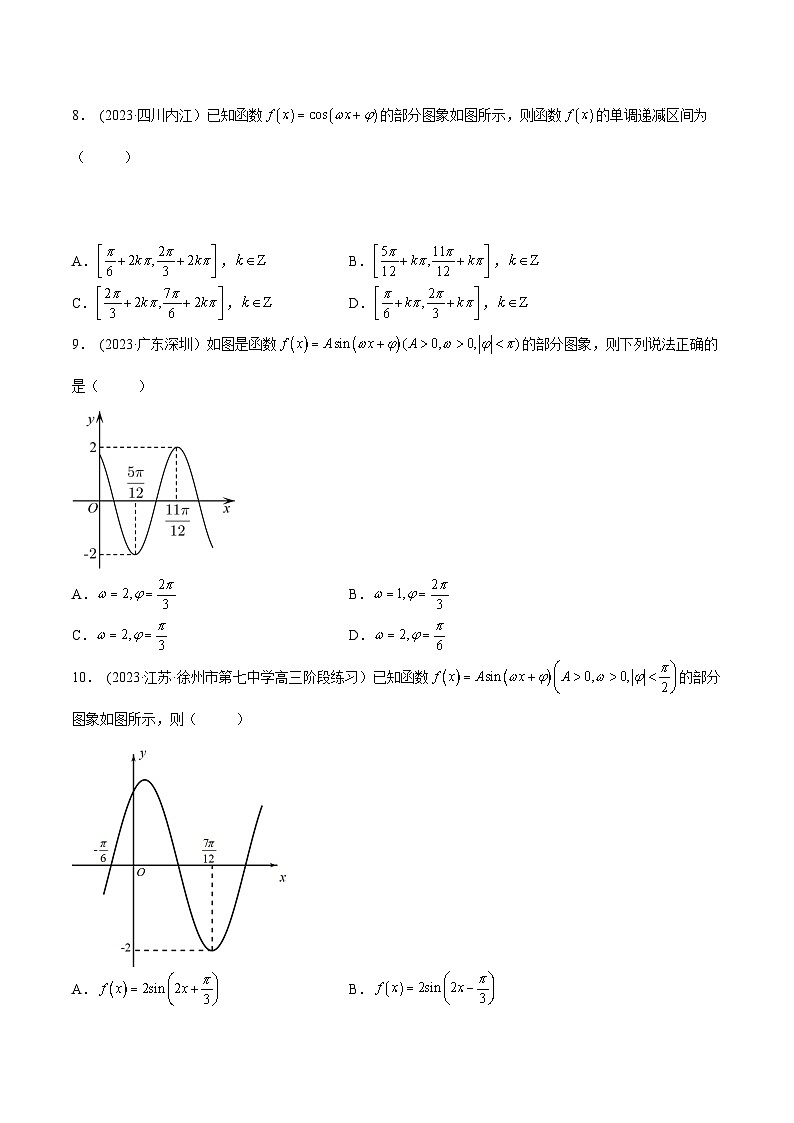
4． (2023·福建福州·高三期末）已知函数的部分图象如图所示，则的单调递增区间为（ ）
A．，B．，
C．，D．，
5． (2023·山西吕梁·一模（文））设函数在的图象大致如图所示，则的最小正周期为（ ）
A．B．C．D．
6． (2023·山西太原）已知函数的部分图象如图所示，则函数的表达式是（ ）
A．B．
C．D．
7． (2023·四川宜宾）函数的部分图象如图所示，则（ ）
A．B．C．D．
8． (2023·四川内江）已知函数的部分图象如图所示，则函数的单调递减区间为（ ）
A．，B．，
C．，D．，
9． (2023·广东深圳）如图是函数的部分图象，则下列说法正确的是（ ）
A．B．
C．D．
10． (2023·江苏·徐州市第七中学高三阶段练习）已知函数的部分图象如图所示，则（ ）
A．B．
C．D．
11． (2023·四川泸州）已知函数的部分图象如图所示，则（ ）
A．，B．，
C．，D．，
12． (2023·北京东城）某同学用“五点法”画函数在一个周期内的简图时，列表如下：
则的解析式为（ ）A．B．
C．D．
13． (2023·河南郑州·高三阶段练习（文））已知函数的部分图象如图所示，则下列说法错误的是（ ）
A．函数
B．函数的图象关于中心对称
C．函数的图象可由函数的图象向左平移个单位得到
D．函数在上单调递减
14． (2023·全国·高三专题练习）已知函数的部分图象如下图所示，若，，将函数的图象向左平移个单位长度后得到函数的图象，则函数的单调递增区间为（ ）
A．B．
C．D．
题组二 定义域
1． (2023·全国·高三专题练习）函数定义域为（ ）
A．B．
C．D．
2． (2023·全国·高三专题练习）函数的定义域为（ ）
A．B．
C．D．
3．（2022·湖南·长沙市明德中学）函数的定义域为
A．B．
C．D．
4．（2022·全国·课时练习）函数的定义域为（ ）
A．B．C．D．
5． (2023·北京市朝阳区人大附中朝阳分校）函数的定义域为__________.
6． (2023·甘肃张掖）函数定义域为____.
7． (2023·全国·高三专题练习）函数的定义域为________________．
8． (2023·陕西·长安一中高三阶段练习）函数的定义域为___________.
9． (2023·全国·高三专题练习）函数的定义域是____________．
10． (2023·全国·高三专题练习）函数的定义域是________.
11．（2022·甘肃）设函数，则的定义域为__________．
题组三 值域
1． (2023·陕西咸阳·二模（理））函数的最小值为（ ）
A．1B．C．D．
2． (2023·宁夏吴忠·模拟预测（文））函数在区间上的最大值是（ ）
A．1B．2C．D．3
3． (2023·北京·模拟预测）已知函数，，则（ ）
A．最大值为2，最小值为1 B．最大值为，最小值为1
C．最大值为，最小值为1 D．最大值为，最小值为
4． (2023·安徽滁州·二模（理））已知函数的最小正周期为，则在区间上的值域为（ ）
A．B．
C．D．
5． (2023·山西·怀仁市第一中学校二模）若将的图象向左平移个单位长度后得到函数的图象，则在上的最小值为（ ）
A．B．
C．D．2
6． (2023·全国·高三开学考试）函数的最大值为( )
A．2B．3C．4D．5
7． (2023·安徽·合肥一中高三阶段练习）将函数f(x)=sinx的图象向右平移个单位长度后得到函数g(x)的图象.则函数y=f(x)·g(x)的最大值为（ ）
A．B．C．D．
8． (2023·北京二中）函数在上的最小值是______.
9． (2023·江苏）已知函数和的图象完全相同，若，则的取值范围是______.
10． (2023·陕西渭南·二模（文））已知函数的部分图象如图所示，则时，函数的值域为___________.
11． (2023·北京·清华附中朝阳学校）已知函数.
(1)求的最小正周期；
(2)求的单调增区间；
(3)函数在区间上的值域为，求实数m的取值范围；
题组四 伸缩平移
1． (2023·重庆巴蜀中学高三阶段练习）将函数的图象向右平移个单位长度得到函数的图象，则（ ）
A．B．
C．D．
2． (2023·广东·高三开学考试）想要得到的图像，只需要将的图像（ ）
A．向左平移个单位B．向右平移个单位
C．向左平移个单位D．向右平移个单位
3． (2023·全国·高三专题练习）要得到的图象，需将的图象（ ）
A．向右平移个单位B．向左平移个单位
C．向右平移个单位D．向左平移个单位
4． (2023·全国·模拟预测）为了得到函数的图象，可以将函数的图象（ ）
A．向左平移个单位B．向右平移个单位
C．向左平移个单位D．向右平移个单位
5． (2023·云南·一模（理））为得到函数的图象，只需要将函数的图象（ ）
A．向左平移个单位B．向左平移个单位
C．向右平移个单位D．向右平移个单位
6． (2023·重庆·模拟预测）已知曲线：的部分图象如图所示，要得到曲线的图象，可将曲线的图象（ ）
A．先向右平移个单位长度，再将各点的横坐标缩短到原来的倍，纵坐标不变
B．先向右平移个单位长度，再将各点的横坐标伸长到原来的2倍，纵坐标不变
C．先向左平移个单位长度，再将各点的横坐标缩短到原来的倍，纵坐标不变
D．先向左平移个单位长度，再将各点的横坐标伸长到原来的2倍，纵坐标不变
7． (2023·江西·临川一中模拟预测）把函数图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数的图象，则（ ）
A．B．C．D．
8． (2023·四川宜宾·二模）已知，将函数的图象向右平移个单位得到，则使得函数是偶函数的的最小值是（ ）
A．B．C．D．
9． (2023·全国·哈师大附中模拟预测）将函数图象上各点的横坐标伸长为原来的2倍，再向右平移个单位，所得图象对应的函数（ ）
A．在区间上单调递增 B．在区间（，）上单调递减
C．图象关于点（，0）对称 D．图象关于直线对称
10． (2023·安徽滁州·二模（文））若将函数图象上各点的横坐标缩短到原来的（纵坐标不变），再向下平移一个单位得到函数的图象，则函数（ ）
A．图象关于点对称B．图象关于对称
C．在上单调递减D．最小正周期是0
x
y
0
2
0
0
3.4.2 三角函数的性质（2）（精练）（基础版）
题组一 解析式
1． (2023·湖北省广水市实验高级中学）若函数（，）的部分图象如图所示，则的值是（ ）
A．B．C．D．
【答案】A
【解析】由图知，A=2，，所以，所以，
则，又图象过点，所以，即，所以，Z，所以Z，因为，所以.故选：A
2 (2023·安徽省宣城中学高三开学考试）已知函数的部分图象如图所示，其中，，则函数的单调递增区间为（ ）
A．B．
C．D．
【答案】C
【解析】由题意得，，则，∴，∴.
∵，∴，又，∴，
∴，令，解得，∴的单调递增区间为.故选：C.
3． (2023·河南·南阳中学）函数的部分图象如图所示，则可能是（ ）
A．B．
C．D．
【答案】A
【解析】由图象可知：，且，所以，不妨设：，将代入得：，即，，解得：，，当时，，故A正确，其他选项均不合要求.故选：A
4． (2023·福建福州·高三期末）已知函数的部分图象如图所示，则的单调递增区间为（ ）
A．，B．，
C．，D．，
【答案】D
【解析】由图象可知，函数的最小正周期满足，
，，，
，得，，
，所以，，
由，，得，，
因此，函数的单调递增区间为，，故选：D.
5． (2023·山西吕梁·一模（文））设函数在的图象大致如图所示，则的最小正周期为（ ）
A．B．C．D．
【答案】A
【解析】由图知，所以，又因为，所以，，所以，，令，解得：或，因为，所以，此时，所以，故选：A
6． (2023·山西太原）已知函数的部分图象如图所示，则函数的表达式是（ ）
A．B．
C．D．
【答案】A
【解析】结合图像和选项可知，，
或.
.故选：A.
7． (2023·四川宜宾）函数的部分图象如图所示，则（ ）
A．B．C．D．
【答案】A
【解析】根据图象可得：
，所以可得的周期为，根据，则有：，
又解得：，根据，
可得：故选：A
8． (2023·四川内江）已知函数的部分图象如图所示，则函数的单调递减区间为（ ）
A．，B．，
C．，D．，
【答案】D
【解析】由图可知，，可得，所以，再由，令，得，所以函数解析式为.由，得，所以函数的单调递减区间为.故选：D
9． (2023·广东深圳）如图是函数的部分图象，则下列说法正确的是（ ）
A．B．
C．D．
【答案】A
【解析】由图像得，，则，，，
得，又，.故选：A.
10． (2023·江苏·徐州市第七中学高三阶段练习）已知函数的部分图象如图所示，则（ ）
A．B．
C．D．
【答案】A
【解析】由图象可知，，所以，
又过点，所以，且
即，所以，即，
又，所以，所以.故选：A.
11． (2023·四川泸州）已知函数的部分图象如图所示，则（ ）
A．，B．，
C．，D．，
【答案】A
【解析】根据函数的图象，A=2，，所以，根据函数在处取得最大值可知，.故选：A.
12． (2023·北京东城）某同学用“五点法”画函数在一个周期内的简图时，列表如下：
则的解析式为（ ）A．B．
C．D．
【答案】D
【解析】由表中数据知：且，则，∴，即，又，可得.∴.故选：D.
13． (2023·河南郑州·高三阶段练习（文））已知函数的部分图象如图所示，则下列说法错误的是（ ）
A．函数
B．函数的图象关于中心对称
C．函数的图象可由函数的图象向左平移个单位得到
D．函数在上单调递减
【答案】D
【解析】将点代入得：，又为对称轴，所以，，故，，因为，所以，故，此时，所以，解得：，函数，A说法正确；
当时，，所以，所以函数的图象关于中心对称，B说法正确；
函数的图象向左平移个单位得到，C说法正确；
时，2x+π3∈2π3,5π3，在2π3,5π3上不单调，故D错误.故选：D
14． (2023·全国·高三专题练习）已知函数的部分图象如下图所示，若，，将函数的图象向左平移个单位长度后得到函数的图象，则函数的单调递增区间为（ ）
A．B．
C．D．
【答案】C
【解析】依题意，，故，故，故，将点代入可得，因为，解得；故，则，令，解得，
故的单调递增区间为.
故选：C
题组二 定义域
1． (2023·全国·高三专题练习）函数定义域为（ ）
A．B．
C．D．
【答案】B
【解析】由函数式知：，∴，即.
故选：B.
2． (2023·全国·高三专题练习）函数的定义域为（ ）
A．B．
C．D．
【答案】A
【解析】函数有意义，则，解得，
所以函数的定义域为.故选：A
3．（2022·湖南·长沙市明德中学）函数的定义域为
A．B．
C．D．
【答案】A
【解析】由题,,故即
解得.即定义域为.故选：A
4．（2022·全国·课时练习）函数的定义域为（ ）
A．B．C．D．
【答案】C
【解析】由得所以.故选：C.
5． (2023·北京市朝阳区人大附中朝阳分校）函数的定义域为__________.
【答案】
【解析】由题意，，所以，．
故答案为：．
6． (2023·甘肃张掖）函数定义域为____.
【答案】∪
【解析】由题意得，即，解得或，从而函数的定义域为∪.故答案为：∪.
7． (2023·全国·高三专题练习）函数的定义域为________________．
【答案】
【解析】，，解得，
对于，当时，，当时，，
当时，，当时，，
∴不等式组的解为：或的定义域为故答案为：
8． (2023·陕西·长安一中高三阶段练习）函数的定义域为___________.
【答案】
【解析】由已知可得，解得，即或.
因此，函数的定义域为.故答案为：.
9． (2023·全国·高三专题练习）函数的定义域是____________．
【答案】
【解析】因为，所以，即，即，解得，故函数的定义域为故答案为：
10． (2023·全国·高三专题练习）函数的定义域是________.
【答案】
【解析】由已知，得，即，则.
因此，函数的定义域为.故答案为：．
11．（2022·甘肃）设函数，则的定义域为__________．
【答案】或
【解析】由题意可知：，
故答案为：或.
题组三 值域
1． (2023·陕西咸阳·二模（理））函数的最小值为（ ）
A．1B．C．D．
【答案】D
【解析】
当时，取得最小值.故选：D
2． (2023·宁夏吴忠·模拟预测（文））函数在区间上的最大值是（ ）
A．1B．2C．D．3
【答案】C
【解析】因为，所以，
，，，．故选：C．
3． (2023·北京·模拟预测）已知函数，，则（ ）
A．最大值为2，最小值为1 B．最大值为，最小值为1
C．最大值为，最小值为1 D．最大值为，最小值为
【答案】B
【解析】，
时，sinx∈[，1]，∴当sinx＝时，f(x)最大值为；当sinx＝1时，f(x)最小值为1.
故选：B.
4． (2023·安徽滁州·二模（理））已知函数的最小正周期为，则在区间上的值域为（ ）
A．B．
C．D．
【答案】C
【解析】
，因为，所以，得，所以，因为，所以，所以当，即时，，当，即时，.故选：C
5． (2023·山西·怀仁市第一中学校二模）若将的图象向左平移个单位长度后得到函数的图象，则在上的最小值为（ ）
A．B．
C．D．2
【答案】C
【解析】因为，又因为，所以，
所以．故选：C
6． (2023·全国·高三开学考试）函数的最大值为( )
A．2B．3C．4D．5
【答案】D
【解析】
∴f(x)最大值为5，故选：D.
7． (2023·安徽·合肥一中高三阶段练习）将函数f(x)=sinx的图象向右平移个单位长度后得到函数g(x)的图象.则函数y=f(x)·g(x)的最大值为（ ）
A．B．C．D．
【答案】A
【解析】由已知可得，
所以，
，.
所以函数的最大值为，故选：A
8． (2023·北京二中）函数在上的最小值是______.
【答案】
【解析】函数，其中锐角由确定，
而，即有，显然在上单调递增，所以当时，.
故答案为：
9． (2023·江苏）已知函数和的图象完全相同，若，则的取值范围是______.
【答案】
【解析】因为，
所以，则.
因为，所以，所以，所以.
故答案为：.
10． (2023·陕西渭南·二模（文））已知函数的部分图象如图所示，则时，函数的值域为___________.
【答案】
【解析】由，，由，，又，解得或，又，，故，，，时，，当时，取得最小值，当时，取得最大值，故值域为.故答案为：.
11． (2023·北京·清华附中朝阳学校）已知函数.
(1)求的最小正周期；
(2)求的单调增区间；
(3)函数在区间上的值域为，求实数m的取值范围；
【答案】(1)；(2)；(3).
【解析】(1)∵，
∴的最小正周期为；
(2)∵， 由，得，
所以的单调增区间是；
(3)∵，，∴，∴，
故实数m的取值范围为.
题组四 伸缩平移
1． (2023·重庆巴蜀中学高三阶段练习）将函数的图象向右平移个单位长度得到函数的图象，则（ ）
A．B．
C．D．
【答案】B
【解析】由题意可知，将函数的图象向左平移个单位长度，可得到函数的图象，
则.故选：B.
2． (2023·广东·高三开学考试）想要得到的图像，只需要将的图像（ ）
A．向左平移个单位B．向右平移个单位
C．向左平移个单位D．向右平移个单位
【答案】B
【解析】因为，将向右平移个单位得到，即；故选：B
3． (2023·全国·高三专题练习）要得到的图象，需将的图象（ ）
A．向右平移个单位B．向左平移个单位
C．向右平移个单位D．向左平移个单位
【答案】D
【解析】，
由向左平移得到.故选：D
4． (2023·全国·模拟预测）为了得到函数的图象，可以将函数的图象（ ）
A．向左平移个单位B．向右平移个单位
C．向左平移个单位D．向右平移个单位
【答案】B
【解析】由题意，，函数，则，所以函数的图象向右平移个单位得到函数的图象，因为函数的周期为，所以向左应该平移个单位.
故选：B.
5． (2023·云南·一模（理））为得到函数的图象，只需要将函数的图象（ ）
A．向左平移个单位B．向左平移个单位
C．向右平移个单位D．向右平移个单位
【答案】D
【解析】因为，
所以，为得到函数的图象，只需要将函数的图象向右平移个单位.
故选：D.
6． (2023·重庆·模拟预测）已知曲线：的部分图象如图所示，要得到曲线的图象，可将曲线的图象（ ）
A．先向右平移个单位长度，再将各点的横坐标缩短到原来的倍，纵坐标不变
B．先向右平移个单位长度，再将各点的横坐标伸长到原来的2倍，纵坐标不变
C．先向左平移个单位长度，再将各点的横坐标缩短到原来的倍，纵坐标不变
D．先向左平移个单位长度，再将各点的横坐标伸长到原来的2倍，纵坐标不变
【答案】A
【解析】因为函数过点，即，又，所以，即，又函数过点，根据五点作图法可知，解得，所以，
由向右平移个单位长度得到，再将各点的横坐标缩短到原来的倍，纵坐标不变得到，即；故选：A
7． (2023·江西·临川一中模拟预测）把函数图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，再把所得曲线向右平移个单位长度，得到函数的图象，则（ ）
A．B．C．D．
【答案】C
【解析】由题意可得图象是由的图象向左平移个单位长度，得，再将其图象上所有点的横坐标缩短为原来的一半，纵坐标不变，可得，即.故选：C.
8． (2023·四川宜宾·二模）已知，将函数的图象向右平移个单位得到，则使得函数是偶函数的的最小值是（ ）
A．B．C．D．
【答案】B
【解析】，
，它为偶函数，
则，，时，取得最小值．故选：B．
9． (2023·全国·哈师大附中模拟预测）将函数图象上各点的横坐标伸长为原来的2倍，再向右平移个单位，所得图象对应的函数（ ）
A．在区间上单调递增 B．在区间（，）上单调递减
C．图象关于点（，0）对称 D．图象关于直线对称
【答案】A
【解析】将函数图象上各点的横坐标伸长为原来的2倍，再向右平移个单位，
得，
因为，所以，故A正确；
因为，所以，故B错误；
，故C错误；
，故D错误；
故选：A
10． (2023·安徽滁州·二模（文））若将函数图象上各点的横坐标缩短到原来的（纵坐标不变），再向下平移一个单位得到函数的图象，则函数（ ）
A．图象关于点对称B．图象关于对称
C．在上单调递减D．最小正周期是
【答案】C
【解析】由题得
对于A当 时,
所以函数的图象不关于点对称，故A错误;
对于B当时， ，
所以函数的图象不关于直线对称，故B错误;
对于C. 令 ，解得: ，
取，得，所以在上单调递减
因为,所以在上单调递减，故C正确
对D. 的最小正周期, 故D错误.故选:C.0
x
y
0
2
0
0