2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法（精讲）（基础版）（原卷版+解析版），共25页。试卷主要包含了裂项相消，错位相减，分组求和，倒序相加等内容，欢迎下载使用。


考点呈现
例题剖析
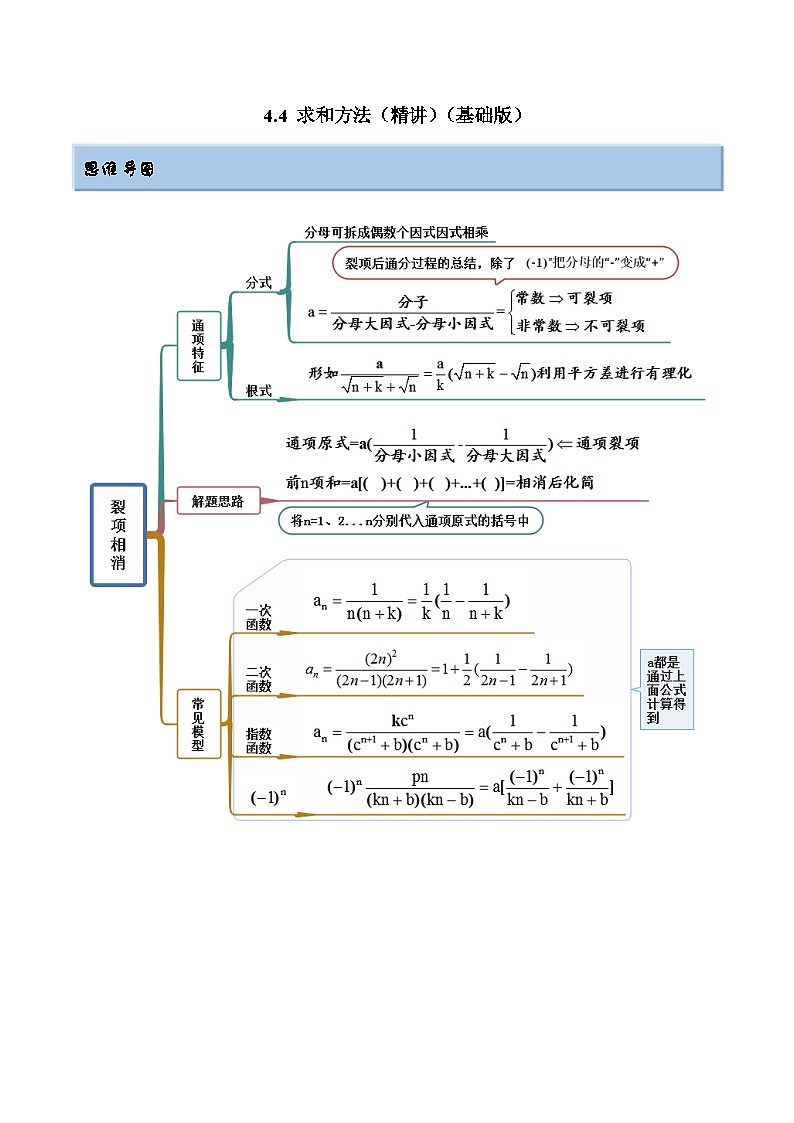
考点一 裂项相消
【例1】 (2023·河南）已知正项数列的前项和为，且．
(1)求的值和数列的通项公式；
(2)设，求数列的前项和．
【一隅三反】
1． (2023·河北保定·一模）已知数列的前项和为，且．
(1)求数列的通项公式；
(2)设，求的前项和．
2． (2023·江西鹰潭·一模）已知正项数列的首项，前n项和满足.
(1)求数列的通项公式；
(2)记数列的前n项和为，若对任意的，不等式恒成立，求实数a的取值范围.
3． (2023·重庆）数列满足：，．
(1)求数列的通项公式；
(2)设，为数列的前n项和，若恒成立，求实数m的取值范围．
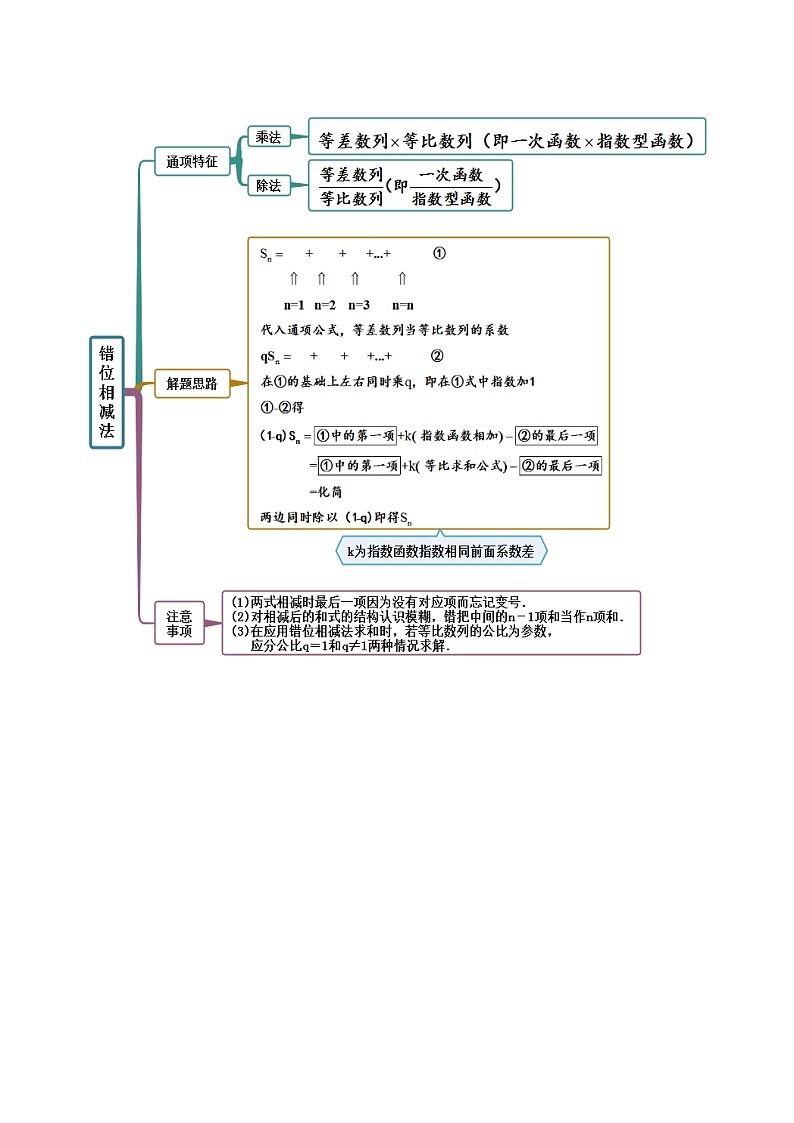
考点二 错位相减
【例2】 (2023·陕西榆林·三模）已知数列的前项和为，且.
(1)求的通项公式；
(2)若，求数列的前项和.
【一隅三反】
1． (2023·河南）已知在数列中，，，．
(1)求的通项公式；
(2)记，求数列的前n项和．
2． (2023·四川省内江市第六中学）已知数列的前项和为，满足，．
(1)求证：数列为等比数列并求数列的通项公式；
(2)设，求前项和．
3． (2023·江西·上饶市第一中学二模）在等差数列中，，.
(1)求数列的通项公式；
(2)设，求数列的前n项和.
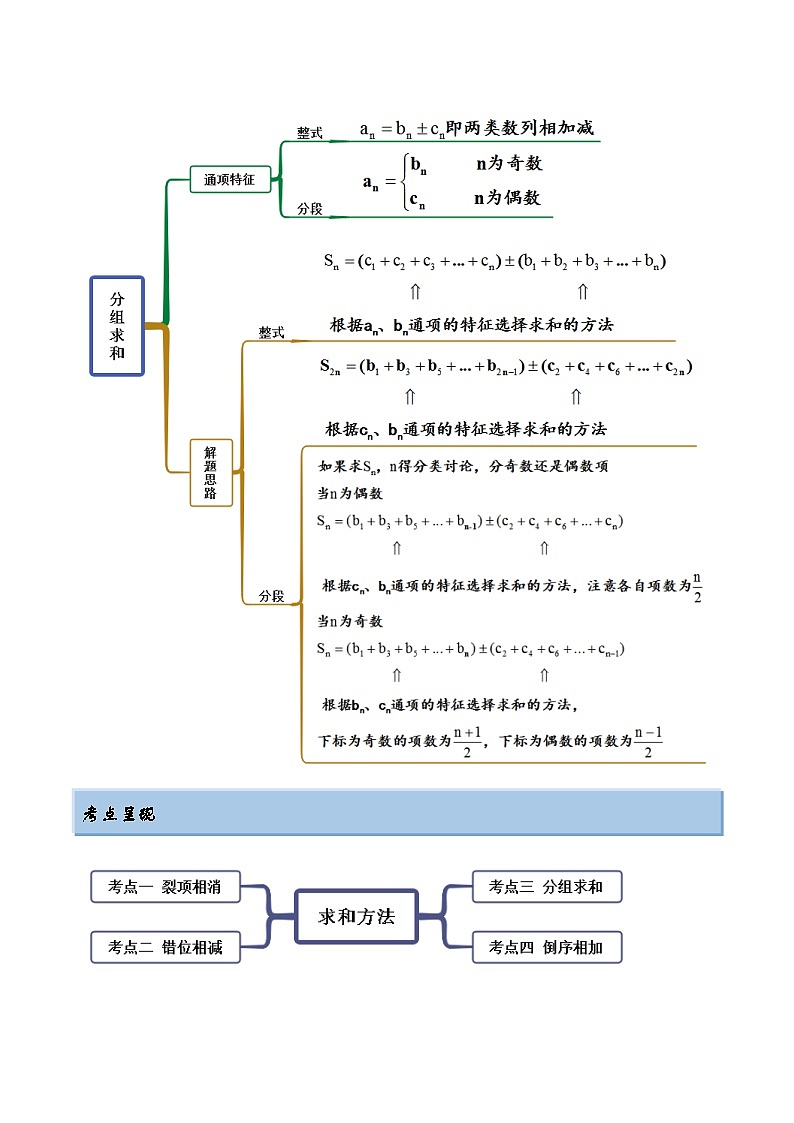
考点三 分组求和
【例3-1】 (2023·甘肃兰州）在①，②是和的等比中项，这两个条件中任选一个，补充在下面问题中，并解答．
问题：已知公差d不为0的等差数列的前n项和为，．
(1)______，求数列的通项公式；
(2)若数列，，求数列的前n项和．
【例3-2】 (2023·福建三明·模拟预测）设数列的前项和为，，，．
(1)求证：是等比数列；
(2)设，求数列的前项和．
【一隅三反】
1． (2023·四川攀枝花）在①，②是，的等差中项，③．这三个条件中任选一个作为已知条件，补充在下面的问题中，然后解答补充完整的题．
已知正项等比数列的前n项和为，，且满足______（只需填序号）．
(1)求数列的通项公式；
(2)设，求数列的前n项和．
注：若选择多个条件分别解答，则按第一个解答计分．
2． (2023·重庆·二模）设为数列的前项和，已知，.若数列满足，，.
(1)求数列和的通项公式；
(2)设，求数列的前项的和.
3． (2023·陕西宝鸡·三模）已知数列中，，且．记﹒
(1)求证：数列是等比数列；
(2)求数列的前n项和．
考点四 倒序相加
【例4】 (2023·全国·高三专题练习）已知函数，利用课本中推导等差数列的前项和的公式的方法，可求得（ ）.
A．25B．26C．13D．
【一隅三反】
1． (2023·全国·高三专题练习）已知若等比数列满足则（ ）
A．B．1010C．2019D．2020
2． (2023·全国·高三专题练习）设函数，利用课本（苏教版必修）中推导等差数列前项和的方法，求得的值为（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）已知函数，数列是正项等比数列，且，______．
4．（2022·全国·高三专题练习）已知函数，________
4.4 求和方法（精讲）（基础版）
思维导图
考点呈现
例题剖析
考点一 裂项相消
【例1】 (2023·河南）已知正项数列的前项和为，且．
(1)求的值和数列的通项公式；
(2)设，求数列的前项和．
【答案】(1)；；(2).
【解析】(1)由得：；
为正项数列，，；
当时，；
当时，；
经检验：满足；.
(2)由（1）得：，
.
【一隅三反】
1． (2023·河北保定·一模）已知数列的前项和为，且．
(1)求数列的通项公式；
(2)设，求的前项和．
【答案】(1)；(2).
【解析】(1)因为，故当时，，
当时，，则，
当时，满足上式，所以.
(2)由（1）得，
所以.
故数列的前项和.
2． (2023·江西鹰潭·一模）已知正项数列的首项，前n项和满足.
(1)求数列的通项公式；
(2)记数列的前n项和为，若对任意的，不等式恒成立，求实数a的取值范围.
【答案】(1)；(2)或.
【解析】(1)当时，，
∴，即，又，
所以数列是首项为1，公差为1的等差数列，故，
又由（），
当时，也适合，所以.
(2)∵，
∴，
又∵对任意的，不等式恒成立，，
∴，解得或.即所求实数的范围是或.
3． (2023·重庆）数列满足：，．
(1)求数列的通项公式；
(2)设，为数列的前n项和，若恒成立，求实数m的取值范围．
【答案】(1)，(2)或
【解析】(1)解：当，，①
，，②
①－②得（*）
在①中令，得，也满足（*），所以，，
(2)解：由（1）知，，
故，
于是，
因为随n的增大而增大，
所以，解得或
所以实数m的取值范围是或.
考点二 错位相减
【例2】 (2023·陕西榆林·三模）已知数列的前项和为，且.
(1)求的通项公式；
(2)若，求数列的前项和.
【答案】(1)；(2).
【解析】(1)当时，，解得.
当时，，整理得，
所以是以9为首项，3为公比的等比数列，故.
(2)由（1）知，，则①，
所以②，
①-②得：，
故.
【一隅三反】
1． (2023·河南）已知在数列中，，，．
(1)求的通项公式；
(2)记，求数列的前n项和．
【答案】(1)(2)
【解析】(1)由题意，可知当时，，故，
当时，，故．综上所述，．
(2)依题意，．
故，
，
两式相减可得，
化简可得．
2． (2023·四川省内江市第六中学）已知数列的前项和为，满足，．
(1)求证：数列为等比数列并求数列的通项公式；
(2)设，求前项和．
【答案】(1)证明见解析，(2)
【解析】(1)，①，当时，②，①减去②得，
，，
可得数列是首项为1，公比为2的等比数列．．
(2)，，
①，②
①减去②得，
．
3． (2023·江西·上饶市第一中学二模）在等差数列中，，.
(1)求数列的通项公式；
(2)设，求数列的前n项和.
【答案】(1)(2)
【解析】(1)设等差数列的公差为，由，，
得：，解得：数列的通项公式为：.
(2)由（1）知：，
所以①
②
①减去②得：
，所以.
考点三 分组求和
【例3-1】 (2023·甘肃兰州）在①，②是和的等比中项，这两个条件中任选一个，补充在下面问题中，并解答．
问题：已知公差d不为0的等差数列的前n项和为，．
(1)______，求数列的通项公式；
(2)若数列，，求数列的前n项和．
【答案】(1)答案见详解；(2)
【解析】(1)选①：由于，
所以，又，所以，故
所以；
选②：是和的等比中项，则，
所以，又，解得，（舍去）
所以；
(2)，，则
【例3-2】 (2023·福建三明·模拟预测）设数列的前项和为，，，．
(1)求证：是等比数列；
(2)设，求数列的前项和．
【答案】(1)证明见解析(2)
【解析】(1)证明：对任意的，，
当时，则有，解得，
当时，由可得，
上述两个等式作差得，所以，，则，
所以，且，所以，数列是等比数列，且首项和公比均为.
(2)解：由（1）可知，所以，，
所以，
.
【一隅三反】
1． (2023·四川攀枝花）在①，②是，的等差中项，③．这三个条件中任选一个作为已知条件，补充在下面的问题中，然后解答补充完整的题．
已知正项等比数列的前n项和为，，且满足______（只需填序号）．
(1)求数列的通项公式；
(2)设，求数列的前n项和．
注：若选择多个条件分别解答，则按第一个解答计分．
【答案】(1)；(2).
【解析】(1)设正项等比数列的公比为，
选①，由，得，
∴，又，
∴，
解得或（舍去），
∴；
选②，是，的等差中项，
∴，又，
∴，即，
∴，
∴；
选③，，
当时，，
∴或（舍去），
∴，
当时，，
故数列的通项公式为；
(2)
∵，
∴，
∴，
∴
.
2． (2023·重庆·二模）设为数列的前项和，已知，.若数列满足，，.
(1)求数列和的通项公式；
(2)设，求数列的前项的和.
【答案】(1)，(2)
【解析】(1)由，①，得：
当时，,解得或（负值舍去），
当时，②，
得：，
所以，所以数列是以3为首项，2为公差的等差数列.
所以.
因为数列满足，，.
所以数列是等比数列，首项为2，公比为2.
所以.
(2)因为，所以，
所以
.
3． (2023·陕西宝鸡·三模）已知数列中，，且．记﹒
(1)求证：数列是等比数列；
(2)求数列的前n项和．
【答案】(1)证明见解析；(2)﹒
【解析】
(1)∵，
且，∴是以2为首项，2为公比的等比数列；
(2)由(1)知，，则，
令的前项和为，
则.
考点四 倒序相加
【例4】 (2023·全国·高三专题练习）已知函数，利用课本中推导等差数列的前项和的公式的方法，可求得（ ）.
A．25B．26C．13D．
【答案】C
【解析】，，即，
设，①
则，②
则①＋②得：，
故.故选：C.
【一隅三反】
1． (2023·全国·高三专题练习）已知若等比数列满足则（ ）
A．B．1010C．2019D．2020
【答案】D
【解析】
等比数列满足
即2020
故选：D
2． (2023·全国·高三专题练习）设函数，利用课本（苏教版必修）中推导等差数列前项和的方法，求得的值为（ ）
A．B．C．D．
【答案】B
【解析】，，
设，
则，
两式相加得，因此，.
故选：B.
3． (2023·全国·高三专题练习）已知函数，数列是正项等比数列，且，______．
【答案】
【解析】由数列是正项等比数列，
且，可得，
因为，
可设，
又，
两式相加可得
，
所以．
故答案为：．
4．（2022·全国·高三专题练习）已知函数，________.
【答案】
【解析】，
，
令，①
，②
①②得：，
，即．
故答案为：.