

- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 5.3 平面向量的应用(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 5.3 平面向量的应用(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.1 抽样方法及特征数(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.2 古典概型及条件概率(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.2 古典概型及条件概率(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.1 抽样方法及特征数(精讲)(基础版)(原卷版+解析版)
展开考点呈现
例题剖析
考点一 抽样方法
【例1-1】(2023·全国·高三专题练习)某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001、002、…、699、700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( )
3321183429 7864560732 5242064438 1223435677 3578905642
8442125331 3457860736 2530073285 2345788907 2368960804
3256780843 6789535577 3489948375 2253557832 4577892345
A.607B.328C.253D.007
【例1-2】 (2023·陕西高三)某乡政府对甲、乙、丙三个村的扶贫对象进行抽样调查,其中甲村30人,乙村25人,丙村40人,用分层抽样的方法抽取19人,则从甲、丙两村共抽取的人数为( )
A.8B.11C.13D.14
【一隅三反】
1. (2023·山东青岛·二模)某校高二年级共有学生1000人,其中男生480人,按性别进行分层,用分层随机抽样的方法从高二全体学生中抽出一个容量为100的样本,若样本按比例分配,则女生应抽取的人数为___________.
2.(2023·全国·高三专题练习)某学校志愿者协会有高一年级120人,高二年级100人,高三年级20人,现用分层抽样的方法从中抽取一个容量为的样本,若从高二年级100人中抽取的人数为10,则___________;
3. (2023·陕西·交大附中模拟预测(文))要考查某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则所抽取样本中第三袋牛奶的编号是_________.(下面摘取了某随机数表的第7行至第9行)
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
考点二 特征数
【例2-1】(2023·全国·高三专题练习)某学校举行诗歌朗诵比赛,10位评委对甲、乙两位同学的表现打分,满分为10分,将两位同学的得分制成如下茎叶图,其中茎叶图茎部分是得分的个位数,叶部分是得分的小数,则下列说法错误的是( )
A.甲同学的平均分大于乙同学的平均分
B.甲、乙两位同学得分的极差分别为2.4和1
C.甲、乙两位同学得分的中位数相同
D.甲同学得分的方差更小
【例2-2】(2023·全国·高三专题练习)某校1000名学生参加数学竞赛,随机抽取了20名学生的考试成绩(单位:分),成绩的频率分布直方图如图所示,则下列说法正确的是( )
A.频率分布直方图中a的值为0.012
B.估计这20名学生数学考试成绩的第60百分位数为80
C.估计这20名学生数学考试成绩的众数为80
D.估计总体中成绩落在内的学生人数为110
【例2-3】(2023·全国·高三专题练习)已知数据,,…,的平均值为,方差为,若数据,,…,的平均值为,方差为,则( ).
A.B.C.D.
【一隅三反】
1.(2023·全国·高三专题练习)如图是2021年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中均为数字中的一个),在去掉一个最高分和一个是低分后,则下列说法错误的是( )
A.甲选手得分的平均数一定大于乙选手得分的平均数
B.甲选手得分的中位数一定大于乙选手得分的中位数
C.甲选手得分的众数与的值无关
D.甲选手得分的方差与的值无关
2. (2023·天津滨海新·模拟预测)某品牌家电公司从其全部200名销售员工中随机抽出50名调查销售情况,销售额都在区间5,25(单位:百万元)内,将其分成5组:5,9,[9,13,13,17,17,21,21,25,并整理得到如下的频率分布直方图,下列说法正确的是( )
A.频率分布直方图中a的值为0.06
B.估计全部销售员工销售额的中位数为15
C.估计全部销售员工中销售额在区间[9,13内有64人
D.估计全部销售员工销售额的第75百分位数为17
3. (2023·全国·模拟预测)(多选)某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取1000名市民对该项目进行评分,统计发现评分均在内,把评分分成,,,,,六组,并绘制成频率分布直方图(如图所示).则下列判断正确的是( )
A.图中a的值为0.025B.该次满意度评分的平均分为85
C.该次满意度评分的众数为85D.大约有34%的市民满意度评分在内
4.(2023·河北·高三阶段练习)(多选)有6个相同的球,分别标有数字1,2,3,4,5,6,现从中有放回的取出5个球并记录取球结果,则下列统计结果中可能取出6号球的是( )
A.平均数为3,中位数为2B.中位数为3,众数为2
C.平均数为2,方差为2.4D.中位数为3,极差为2
5. (2023·四川成都·高三期末(理))若数据9,m,6,n,5的平均数为7,方差为2,则数据11,9,,17,的平均数和方差分别为( )
A.13,4B.14,4C.13,8D.14,8
考点三 抽样方法与特征数综合
【例3】 (2023·全国·高三专题练习)某区政府组织了以“不忘初心,牢记使命”为主题的教育活动,为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n名,获得了他们一周参与主题教育活动时间(单位:h)的频率分布直方图如图所示,已知参与主题教育活动时间在内的人数为92.
(1)求n的值;
(2)以每组数据所在区间的中点值作为本组的代表,估算这些党员干部参与主题教育活动时间的中位数(中位数精确到0.01).
(3)如果计划对参与主题教育活动时间在内的党员干部给予奖励,且在,内的分别评为二等奖和一等奖,那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动,再从这5人中随机抽取2人作为主宣讲人,求这2人均是二等奖的概率.
【一隅三反】
1 (2023·新疆克拉玛依·三模(文))第届北京冬季奥林匹克运动会于年月日至月日在北京和张家口联合举办.这是中国历史上第一次举办冬季奥运会,它掀起了中国人民参与冬季运动的大热潮.某市举办了中学生滑雪比赛,从中抽取名学生的测试分数绘制成茎叶图和频率分布直方图如下,后来茎叶图受到了污损,可见部分信息如图.
(1)求频率分布直方图中的值,并根据直方图估计该市全体中学生的测试分数的平均数(同一组中的数据以这组数据所在区间中点的值作代表,结果保留一位小数);
(2)现要对测试成绩在前26%的中学生颁发“滑雪达人”证书,并制定出能够获得证书的测试分数线,请你用样本来估计总体,给出这个分数线的估计值.
2. (2023·全国·高三专题练习)甲、乙两台机床同时生产一种零件,在10天中,两台机床每天生产的次品数分别为:
甲
乙
(1)分别计算这两组数据的平均数和标准差;
(2)由(1)的计算结果,分析哪台机床的性能更好.
3. (2023·青海·海东市第一中学模拟预测(文))新高考取消文理分科,采用选科模式,这赋予了学生充分的自由选择权.新高考地区某校为了解本校高一年级将来高考选考历史的情况,随机选取了100名高一学生的某次历史测试成绩(满分100分),把其中不低于50分的分成五段,,…,后画出如图所示的部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求出这100名学生中历史成绩低于50分的人数.
(2)根据调查,本次历史测试成绩不低于70分的学生,高考将选考历史科目;成绩低于70分的学生,高考将选考物理科目.按分层抽样的方法从测试成绩在,的学生中选取5人,再从这5人中任意选取2人,求这2人高考都选考历史科目的概率.
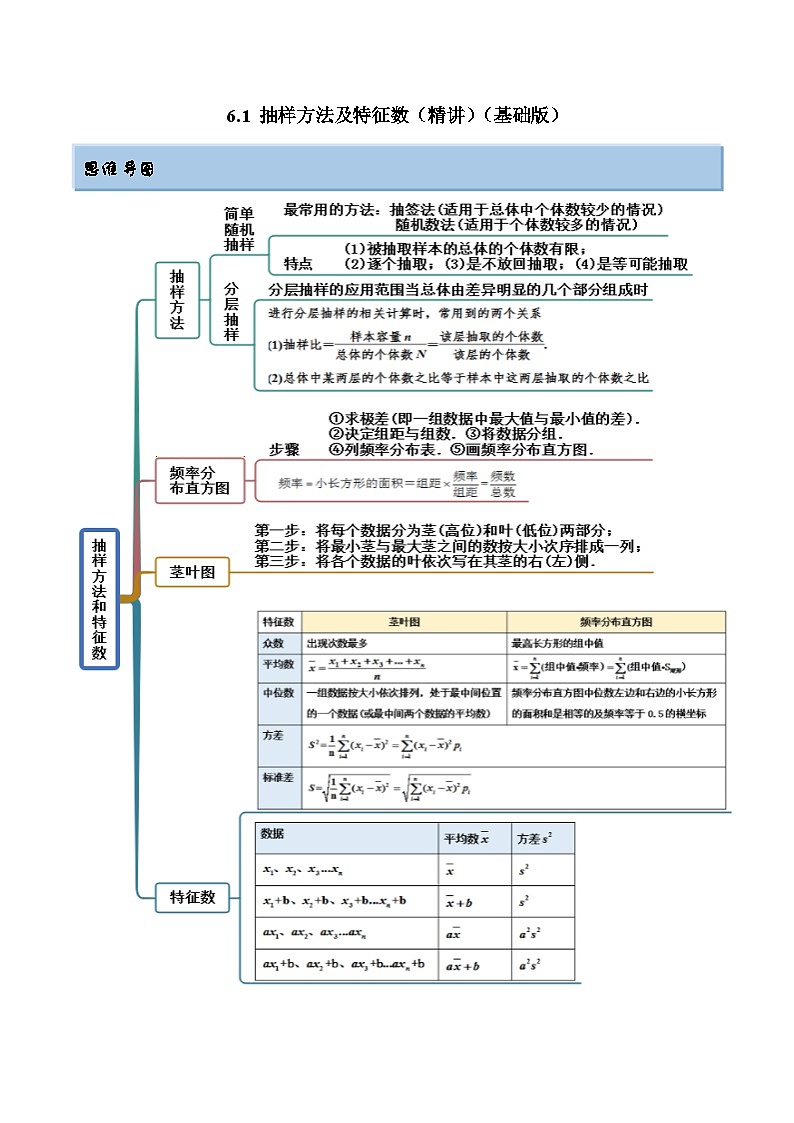
6.1 抽样方法及特征数(精讲)(基础版)
思维导图
考点呈现
例题剖析
考点一 抽样方法
【例1-1】(2023·全国·高三专题练习)某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号001、002、…、699、700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第5个样本编号是( )
3321183429 7864560732 5242064438 1223435677 3578905642
8442125331 3457860736 2530073285 2345788907 2368960804
3256780843 6789535577 3489948375 2253557832 4577892345
A.607B.328C.253D.007
【答案】B
【解析】从表中第5行第6列开始向右读取数据,得到的数据中有两个超出范围,一个重复,
抽取的5个样本编号分别是:253,313,457,007,328,所以得到的第5个样本编号是328.
选:B
【例1-2】 (2023·陕西高三)某乡政府对甲、乙、丙三个村的扶贫对象进行抽样调查,其中甲村30人,乙村25人,丙村40人,用分层抽样的方法抽取19人,则从甲、丙两村共抽取的人数为( )
A.8B.11C.13D.14
【答案】D
【解析】设甲、丙两村抽取的人数分别为、.
依题意得,解得,,所以.故选:D.
【一隅三反】
1. (2023·山东青岛·二模)某校高二年级共有学生1000人,其中男生480人,按性别进行分层,用分层随机抽样的方法从高二全体学生中抽出一个容量为100的样本,若样本按比例分配,则女生应抽取的人数为___________.
【答案】52
【解析】由分层抽样的性质得:女生应该抽取:.故答案为:52.
2.(2023·全国·高三专题练习)某学校志愿者协会有高一年级120人,高二年级100人,高三年级20人,现用分层抽样的方法从中抽取一个容量为的样本,若从高二年级100人中抽取的人数为10,则___________;
【答案】24
【解析】由题意,,可得.故答案为:24
3. (2023·陕西·交大附中模拟预测(文))要考查某公司生产的500克袋装牛奶的质量是否达标,现从500袋牛奶中抽取50袋进行检验,将它们编号为000,001,002,…499,利用随机数表抽取样本,从第8行第5列的数开始,按3位数依次向右读取,到行末后接着从下一行第一个数继续.则所抽取样本中第三袋牛奶的编号是_________.(下面摘取了某随机数表的第7行至第9行)
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
【答案】169
【解析】从第8行第5列的数开始向右读,第一个数为583,不符合条件,第二个数为921,不符合条件,第三个数为206,符合条件,以下依次为:766,301,647,859,169,555,其中766,647,859,不符合条件,故第三个数为169.
考点二 特征数
【例2-1】(2023·全国·高三专题练习)某学校举行诗歌朗诵比赛,10位评委对甲、乙两位同学的表现打分,满分为10分,将两位同学的得分制成如下茎叶图,其中茎叶图茎部分是得分的个位数,叶部分是得分的小数,则下列说法错误的是( )
A.甲同学的平均分大于乙同学的平均分
B.甲、乙两位同学得分的极差分别为2.4和1
C.甲、乙两位同学得分的中位数相同
D.甲同学得分的方差更小
【答案】D
【解析】对于甲,
对于乙,故正确.
甲的极差,乙的极差故正确.
甲得分的中位数,乙得分的中位数,故正确.
对于甲,
对于乙,
故错误.故选.
【例2-2】(2023·全国·高三专题练习)某校1000名学生参加数学竞赛,随机抽取了20名学生的考试成绩(单位:分),成绩的频率分布直方图如图所示,则下列说法正确的是( )
A.频率分布直方图中a的值为0.012
B.估计这20名学生数学考试成绩的第60百分位数为80
C.估计这20名学生数学考试成绩的众数为80
D.估计总体中成绩落在内的学生人数为110
【答案】B
【解析】由可得,故A错误
前三个矩形的面积和为,所以这20名学生数学考试成绩的第60百分位数为80,故B正确这20名学生数学考试成绩的众数为,故C错误
这20名学生数学考试成绩落在内的学生人数为,则总体中成绩落在内的学生人数为,故D错误故选:B
【例2-3】(2023·全国·高三专题练习)已知数据,,…,的平均值为,方差为,若数据,,…,的平均值为,方差为,则( ).
A.B.C.D.
【答案】A
【解析】因为,,…,的平均值为,方差为,
由数据,,…,的平均值为,方差为,
所以,解得,.故选:A.
【一隅三反】
1.(2023·全国·高三专题练习)如图是2021年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中均为数字中的一个),在去掉一个最高分和一个是低分后,则下列说法错误的是( )
A.甲选手得分的平均数一定大于乙选手得分的平均数
B.甲选手得分的中位数一定大于乙选手得分的中位数
C.甲选手得分的众数与的值无关
D.甲选手得分的方差与的值无关
【答案】C
【解析】由题意,甲选手得分的平均数,
乙选手得分的平均数,故选项A正确;
无论为何值,甲选手得分的中位数一定是85,乙选手得分的中位数是84,故选项B正确;
当时,甲选手得分的众数为81,85,当时,甲选手得分的众数为85,故选项C不正确;
因为是最高分,被去掉,故甲选手得分的方差与的值无关,故选项D正确;故选:C.
2. (2023·天津滨海新·模拟预测)某品牌家电公司从其全部200名销售员工中随机抽出50名调查销售情况,销售额都在区间5,25(单位:百万元)内,将其分成5组:5,9,[9,13,13,17,17,21,21,25,并整理得到如下的频率分布直方图,下列说法正确的是( )
A.频率分布直方图中a的值为0.06
B.估计全部销售员工销售额的中位数为15
C.估计全部销售员工中销售额在区间[9,13内有64人
D.估计全部销售员工销售额的第75百分位数为17
【答案】C
【解析】由频率分布直方图可得,解得,故A错误;
估计其全部销售员工中销售额在区间内的人数为:(人),故C正确;
设中位数为,则,解得,故B错误;
因为,故为第百分位数,故D错误;故选:C
3. (2023·全国·模拟预测)(多选)某城市地铁交通建设项目已经基本完成,为了解市民对该项目的满意度,分别从不同地铁站点随机抽取1000名市民对该项目进行评分,统计发现评分均在内,把评分分成,,,,,六组,并绘制成频率分布直方图(如图所示).则下列判断正确的是( )
A.图中a的值为0.025B.该次满意度评分的平均分为85
C.该次满意度评分的众数为85D.大约有34%的市民满意度评分在内
【答案】ACD
【解析】由频率分布直方图知,由得,故A正确;因为,所以满意度的平均分为80.7,故B错误;由频率分布图可知众数估计为85,故C正确;,由样本估计总体可以认为约有34%的市民评分在内,故D正确.故答案为:ACD.
4.(2023·河北·高三阶段练习)(多选)有6个相同的球,分别标有数字1,2,3,4,5,6,现从中有放回的取出5个球并记录取球结果,则下列统计结果中可能取出6号球的是( )
A.平均数为3,中位数为2B.中位数为3,众数为2
C.平均数为2,方差为2.4D.中位数为3,极差为2
【答案】AB
【解析】对于A:若取出的5个球为1、1、2、5、6时,满足平均数为3,中位数为2,可以出现6号球,故A正确;
对于B:若取出的5个球为2、2、3、4、6时,满足中位数为3,众数为2,可以出现6号球,故B正确;
对于C:若平均数为2,方差为2.4,则方差,所以不能出现6号球,故C错误;
对于D:若中位数为3,极差为2,则取出的最大号为5,不能出现6号球,故D错误;
故选:AB.
5. (2023·四川成都·高三期末(理))若数据9,m,6,n,5的平均数为7,方差为2,则数据11,9,,17,的平均数和方差分别为( )
A.13,4B.14,4C.13,8D.14,8
【答案】C
【解析】数据9,m,6,n,5的平均数为,
方差为,
化简得 ,解得或,
或,
则数据11,9,,17,为或,
两组数据有相同的平均数和方差,
平均数为,
方差为,
故选:C
考点三 抽样方法与特征数综合
【例3】 (2023·全国·高三专题练习)某区政府组织了以“不忘初心,牢记使命”为主题的教育活动,为统计全区党员干部一周参与主题教育活动的时间,从全区的党员干部中随机抽取n名,获得了他们一周参与主题教育活动时间(单位:h)的频率分布直方图如图所示,已知参与主题教育活动时间在内的人数为92.
(1)求n的值;
(2)以每组数据所在区间的中点值作为本组的代表,估算这些党员干部参与主题教育活动时间的中位数(中位数精确到0.01).
(3)如果计划对参与主题教育活动时间在内的党员干部给予奖励,且在,内的分别评为二等奖和一等奖,那么按照分层抽样的方法从获得一、二等奖的党员干部中选取5人参加社区义务宣讲活动,再从这5人中随机抽取2人作为主宣讲人,求这2人均是二等奖的概率.
【答案】(1)(2)(3)
【解析】(1)由已知可得,.
则,得.
(2)设中位数为,则,得.
(3)按照分层抽样的方法从,内选取的人数为,
从,内选取的人数为.
记二等奖的4人分别为,,,,一等奖的1人为,
事件为“从这5人中抽取2人作为主宣讲人,且这2人均是二等奖”.
从这5人中随机抽取2人的基本事件为,,,,,,,,,,共10种,
其中2人均是二等奖的情况有,,,,,,共6种,
由古典概型的概率计算公式得.
【一隅三反】
1 (2023·新疆克拉玛依·三模(文))第届北京冬季奥林匹克运动会于年月日至月日在北京和张家口联合举办.这是中国历史上第一次举办冬季奥运会,它掀起了中国人民参与冬季运动的大热潮.某市举办了中学生滑雪比赛,从中抽取名学生的测试分数绘制成茎叶图和频率分布直方图如下,后来茎叶图受到了污损,可见部分信息如图.
(1)求频率分布直方图中的值,并根据直方图估计该市全体中学生的测试分数的平均数(同一组中的数据以这组数据所在区间中点的值作代表,结果保留一位小数);
(2)现要对测试成绩在前26%的中学生颁发“滑雪达人”证书,并制定出能够获得证书的测试分数线,请你用样本来估计总体,给出这个分数线的估计值.
【答案】(1),平均数为(2)
【解析】(1)由频率分布直方图可知,测试分数位于的频率为,
则测试分数位于个数为,
所以,测试分数位于的个数为,
所以.
估计平均数为.
(2)因为测试分数位于的频率为,测试分数位于的频率为,
能够获得“滑雪达人”证书的中学生测试分数要在前,
故设能够获得证书的测试分数线为,则,
由,可得,所以分数线的估计值为.
2. (2023·全国·高三专题练习)甲、乙两台机床同时生产一种零件,在10天中,两台机床每天生产的次品数分别为:
甲
乙
(1)分别计算这两组数据的平均数和标准差;
(2)由(1)的计算结果,分析哪台机床的性能更好.
【答案】(1)甲:, ,乙:,(2)乙机床性能更好
【解析】(1)记甲组数据的平均数和标准差分别为,乙组数据的平均数和标准差分别为
则
(2)由(1)知,所以甲机床生产出的次品数高于乙机床生产出的次品数;又,所以乙机床的性能比甲机床的性能更加稳定.
综上,乙机床性能比甲机床稳定,且生产的次品数更低,所以乙机床的性能更好.
3. (2023·青海·海东市第一中学模拟预测(文))新高考取消文理分科,采用选科模式,这赋予了学生充分的自由选择权.新高考地区某校为了解本校高一年级将来高考选考历史的情况,随机选取了100名高一学生的某次历史测试成绩(满分100分),把其中不低于50分的分成五段,,…,后画出如图所示的部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求出这100名学生中历史成绩低于50分的人数.
(2)根据调查,本次历史测试成绩不低于70分的学生,高考将选考历史科目;成绩低于70分的学生,高考将选考物理科目.按分层抽样的方法从测试成绩在,的学生中选取5人,再从这5人中任意选取2人,求这2人高考都选考历史科目的概率.
【答案】(1)10(2)
【解析】(1)因为各组的频率和等于1,所以低于50分的频率为,
所以低于50分的人数为.
(2)由(1)可知,学生成绩在的频数为,学生成绩在的频数为.按分层抽样的方法从中选取5人,则成绩在的学生被抽取人,分别记为,,成绩在的学生被抽取人,分别记为,,.
从中任意选取2人,有,,,,,,,,,这10种选法,其中高考都选考历史科目的选法有,,3种.
所以这2人高考都选考历史科目的概率为.
2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.1 抽样方法及特征数(精练)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 6.1 抽样方法及特征数(精练)(基础版)(原卷版+解析版),共24页。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精讲)(基础版)(原卷版+解析版),共25页。试卷主要包含了裂项相消,错位相减,分组求和,倒序相加等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.2 等比数列(精讲)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.2 等比数列(精讲)(基础版)(原卷版+解析版),共23页。试卷主要包含了等比数列基本量的计算,等比中项,等比数列前n项和的性质,等比数列定义及其运用,等比数列的实际应用等内容,欢迎下载使用。












