2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角（精讲）（基础版）（原卷版+解析版），共21页。试卷主要包含了线线角，线面角，二面角等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 线线角
【例1】 (2023·内蒙古赤峰）在正方体中，，分别为，的中点，则异面直线与所成角的余弦值是（ ）
A．B．C．D．
【一隅三反】
1． (2023·吉林长春·模拟预测（理））在矩形ABCD中，O为BD中点且，将平面ABD沿对角线BD翻折至二面角为90°，则直线AO与CD所成角余弦值为（ ）
A．B．
C．D．
2． (2023·河南）在正方体中，E，F分别为棱AD，的中点，则异面直线EF与所成角的余弦值为（ ）．
A．B．
C．D．
考点二 线面角
【例2】（2023·全国·高三专题练习）如图，三棱台中，，，．
(1)证明：；
(2)求直线与平面所成的角．
【一隅三反】
1．（2023·全国·高三专题练习（理））在四棱锥中，底面．
(1)证明：；
(2)求PD与平面所成的角的正弦值．
2．（2023·全国·高三专题练习（理））如图，在三棱柱中，，．
(1)证明：平面平面．
(2)设P是棱的中点，求AC与平面所成角的正弦值．
3． (2023·内蒙古·海拉尔第二中学模拟预测（理））已知四棱锥中，四边形为菱形，，
(1)求证：是等边三角形；
(2)若，求与平面所成角的正弦值.
考点三 二面角
【例3】 (2023·青海·海东市第一中学）如图，在四棱锥P－ABCD中，平面平面ABCD，为等边三角形，，，M是棱上一点，且.
(1)求证：平面MBD；
(2)求二面角M－BD－C的余弦值.
【一隅三反】
1． (2023·全国·模拟预测）在四棱锥中，平面，四边形是矩形，分别是的中点．
(1)求证：平面；
(2)求二面角的余弦值．
2． (2023·四川成都）如图，在三棱锥中，已知平面ABC，，，D为PC上一点，且，．
(1)求AC的长；
(2)若E为AC的中点，求二面角的余弦值．
3． (2023·全国·模拟预测（理））图1是由矩形，和菱形组成的一个平面图形，其中，，．将该图形沿，折起使得与重合，连接，如图2．
(1)证明：图2中C，D，E，G四点共面；
(2)求图2中二面角的平面角的余弦值．
7.5 空间向量求空间角（精讲）（基础版）
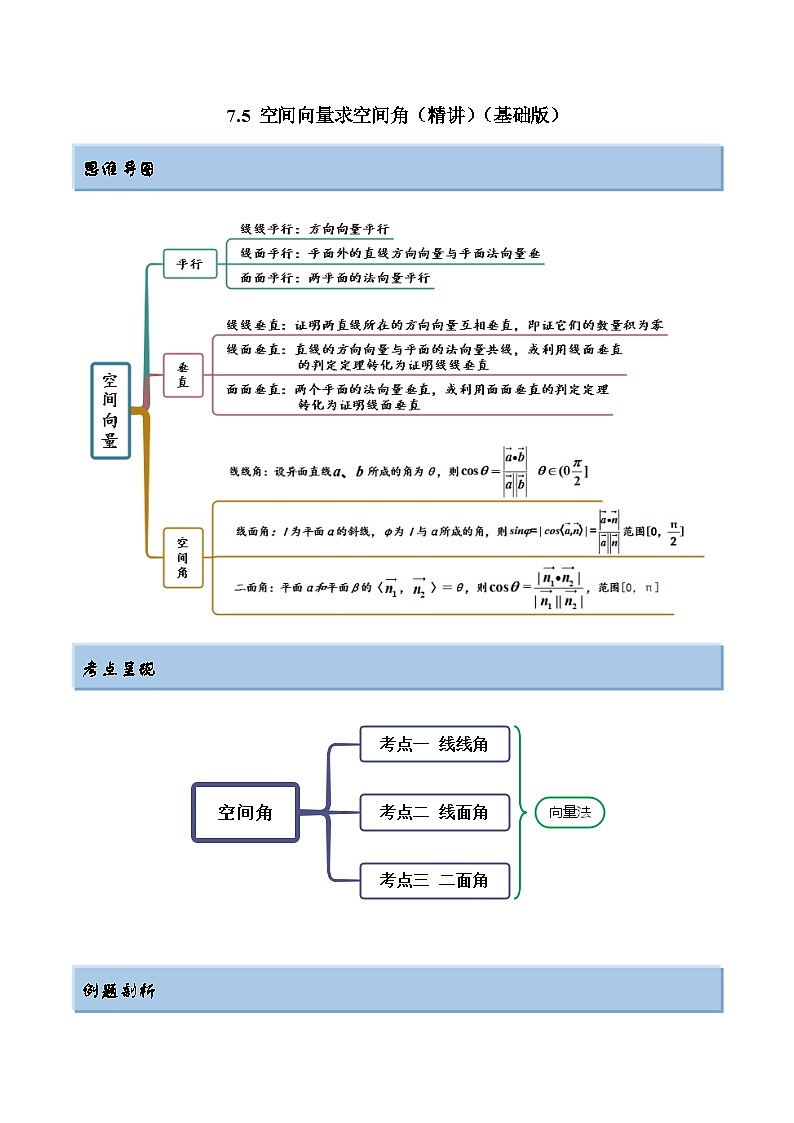
思维导图
考点呈现
例题剖析
考点一 线线角
【例1】 (2023·内蒙古赤峰）在正方体中，，分别为，的中点，则异面直线与所成角的余弦值是（ ）
A．B．C．D．
【答案】A
【解析】如图，以AB、AD、分别为x、y、z轴，建立空间直角坐标系，设正方体棱长为2，则
则因为
所以异面直线与所成角的余弦值为.故选：A
【一隅三反】
1． (2023·吉林长春·模拟预测（理））在矩形ABCD中，O为BD中点且，将平面ABD沿对角线BD翻折至二面角为90°，则直线AO与CD所成角余弦值为（ ）
A．B．
C．D．
【答案】C
【解析】在平面中过作，垂足为；
在平面中过作，垂足为.
由于平面平面，且交线为，
所以平面，平面，
设，
，
同理可得，
以为原点，建立如图所示空间直角坐标系，
则，
，
设与所成角为，
则.
故选：C
2． (2023·河南）在正方体中，E，F分别为棱AD，的中点，则异面直线EF与所成角的余弦值为（ ）．
A．B．C．D．
【答案】A
【解析】如图建立空间直角坐标系，设正方体的棱长为2，
则，
∴，
∴，
即异面直线EF与所成角的余弦值为.故选：A.
考点二 线面角
【例2】（2023·全国·高三专题练习）如图，三棱台中，，，．
(1)证明：；
(2)求直线与平面所成的角．
【答案】(1)证明见解析(2)
【解析】（1）由题，取中点，连接，由，，则，又面，故面，因为面，故，又，则，得证；
由题，，则，又，，故，故.分别以为轴建立如图空间直角坐标系，易得，，，，，，设平面法向量，则，令，则，故，故直线与平面所成的角为.即直线与平面所成的角为.
【一隅三反】
1．（2023·全国·高三专题练习（理））在四棱锥中，底面．
(1)证明：；
(2)求PD与平面所成的角的正弦值．
【答案】(1)证明见解析；(2).
【解析】(1)证明：在四边形中，作于，于，
因为，
所以四边形为等腰梯形，
所以，
故，，
所以，
所以，
因为平面，平面，
所以，
又，
所以平面，
又因为平面，
所以；
(2)
解：如图，以点为原点建立空间直角坐标系，
，
则，
则，
设平面的法向量，
则有，可取，
则，
所以与平面所成角的正弦值为.
2．（2023·全国·高三专题练习（理））如图，在三棱柱中，，．
(1)证明：平面平面．
(2)设P是棱的中点，求AC与平面所成角的正弦值．
【答案】(1)证明见解析(2)
【解析】(1)设．在四边形中，∵，，连接，
∴由余弦定理得，即，
∵，∴．
又∵，∴，，∴平面，
∵平面，∴平面平面．
(2)取AB中点D，连接CD，∵，∴，
由（1）易知平面，且．
如图，以B为原点，分别以射线BA，为x，y轴的正半轴，建立空间直角坐标系B-xyz，
则，，，，，．
，，
设平面的法向量为，则，
得，令，则取，
，，
AC与平面所成角的正弦值为．
3． (2023·内蒙古·海拉尔第二中学模拟预测（理））已知四棱锥中，四边形为菱形，，
(1)求证：是等边三角形；
(2)若，求与平面所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】(1)证明：取的中点，连接、，
因为，为的中点，则，
因为，，平面，
平面，则，故，
因为四边形为菱形，则，所以，，
因此，为等边三角形.
(2)解：由已知，，则，，
为的中点，所以，，
因为是边长为的等边三角形，则，
因为，则，，
因为平面，以点为坐标原点，、、所在直线分别为、、轴建立如下图所示的空间直角坐标系，
则、、、，
设平面的法向量为，，，
则，取，可得，
，.
因此，与平面所成角的正弦值为.
考点三 二面角
【例3】 (2023·青海·海东市第一中学）如图，在四棱锥P－ABCD中，平面平面ABCD，为等边三角形，，，M是棱上一点，且.
(1)求证：平面MBD；
(2)求二面角M－BD－C的余弦值.
【答案】(1)证明见解析(2)
【解析】(1)连接AC，记AC与BD的交点为H，连接MH.
由，得，，又，则，
∴，又平面MBD，平面MBD，
∴平面MBD.
(2)记O为CD的中点，连接PO，BO.
∵为等边三角形，∴，
∵平面平面ABCD，平面平面ABCD＝CD，
∴平面ABCD.
以O为原点，OB为x轴，OC为y轴，OP为x轴，建立空间直角坐标系，如下图，
则，，，，，
，.
设平面BDM的法向量，则，
取x＝1得，
平面BCD的一个法向量.
设二面角M－BD－C的平面角为θ，则.
∴二面角M－BD－C的余弦值为.
【一隅三反】
1． (2023·全国·模拟预测）在四棱锥中，平面，四边形是矩形，分别是的中点．
(1)求证：平面；
(2)求二面角的余弦值．
【答案】(1)证明见解析(2)
【解析】(1)证明：取的中点，连接，，
又是的中点，所以，且．
因为四边形是矩形，所以且，所以，且．
因为是的中点，所以，所以且，
所以四边形是平行四边形，故．
因为平面，平面，
所以平面．
(2)因为平面，四边形是矩形，所以，，两两垂直，
以点为坐标原点，直线，，分别为轴，轴，轴建立空间直角坐标系（如图所示）．
设，所以，．
因为，分别为，的中点，
所以，，，
所以，，．
设平面的一个法向量为，
由即
令，则，，所以．
设平面的一个法向量为，
由即
令，则，，
所以．
所以．
由图知二面角为锐角，
所以二面角的余弦值为．
2． (2023·四川成都）如图，在三棱锥中，已知平面ABC，，，D为PC上一点，且，．
(1)求AC的长；
(2)若E为AC的中点，求二面角的余弦值．
【答案】(1)(2)
【解析】(1)∵平面ABC，AB，平面ABC，∴，．
又，
∴以A为坐标原点，，，的方向分别为x轴，y轴，z轴正方向，建立如图所示的空间直角坐标系．
则，，设．则，．
由，得，则．
∵，即，∴，即．
又，解得．∴AC的长为．
(2)∵E为AC的中点，由（Ⅰ）知，．
则，．
设平面DBE的一个法向量为．
由得令，得∴．
设平面ABE的一个法向量为．
设二面角的平面角为．
∵，易知二面角为锐角，
∴二面角的余弦值为．
3． (2023·全国·模拟预测（理））图1是由矩形，和菱形组成的一个平面图形，其中，，．将该图形沿，折起使得与重合，连接，如图2．
(1)证明：图2中C，D，E，G四点共面；
(2)求图2中二面角的平面角的余弦值．
【答案】(1)证明见解析(2)
【解析】(1)证明：∵四边形和分别是矩形和菱形，
∴，，
∴，
∴，，，四点共面．
(2)解：在平面内过点作，以为原点，，，所在直线分别为，，轴，建立如图所示空间直角坐标系，
则，，，．
∴，，，．
设平面的一个法向量为，则，即．
令，则．∴．
设平面的一个法向量为．则，令，可得．
∴，显然二面角为锐角．
∴二面角的平面角的余弦值为．