

所属成套资源:2024年新高考专用数学第一轮复习精品讲义一隅三反(原卷版+解析版)
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.5 空间向量求空间角(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.7 空间几何的外接球(精讲)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.7 空间几何的外接球(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考专用数学第一轮复习讲义一隅三反基础版 8.1 定义域(精练)(基础版)(原卷版+解析版) 试卷 0 次下载
2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精练)(基础版)(原卷版+解析版)
展开
这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 7.6 空间向量求空间距离(精练)(基础版)(原卷版+解析版),共34页。
A.B.1C.D.
2. (2023·山东)点是直线上一点,是直线的一个方向向量,则点到直线的距离是______.
3. (2023云南)如图,已知三棱柱的棱长均为2,,.
(1)证明:平面平面ABC;
(2)设M为侧棱上的点,若平面与平面ABC夹角的余弦值为,求点M到直线距离.
题组二 点面距
1. (2023·新疆)如图所示,在四棱锥中,平面,,在四边形中,,,,点在上,,与平面成的角.
(1)求证:平面;
(2)点到平面的距离.
2. (2023·重庆一中)已知四棱锥S-ABCD的底面是正方形,平面ABCD,求证:
(1)平面SAC;
(2)若,求点C到平面SBD的距离.
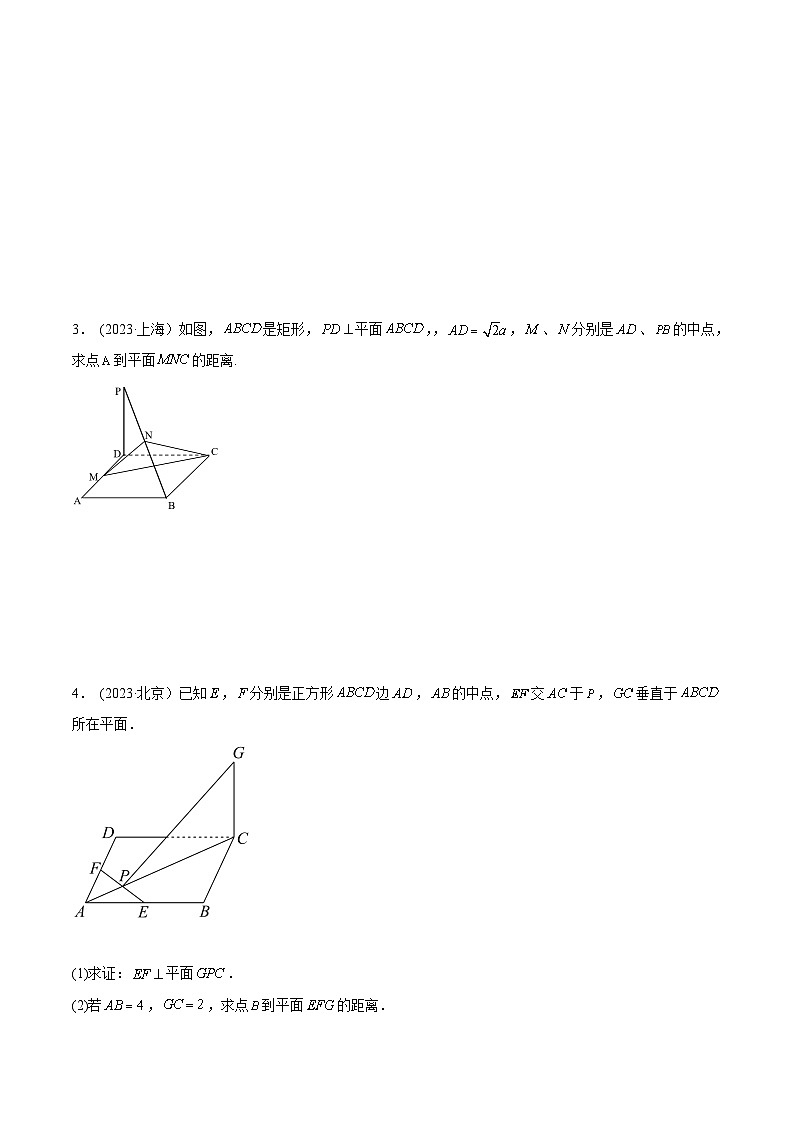
3. (2023·上海)如图,是矩形,平面,,,、分别是、的中点,求点到平面的距离.
4. (2023·北京)已知,分别是正方形边,的中点,交于,垂直于所在平面.
(1)求证:平面.
(2)若,,求点到平面的距离.
5.(2023·全国·高三专题练习)在如图所示的五面体中,面是边长为2的正方形,平面,,且,为的中点.
(1)求证:平面;
(2)求二面角的余弦值;
(3)求点到平面的距离.
6. (2023·湖南·周南中学)某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E、F、G分别是正方形的三边AB、CD、AD的中点,先沿着虚线段FG将等腰直角三角形FDG裁掉,再将剩下的五边形ABCFG沿着线段EF折起,连接AB、CG就得到了一个“刍甍”(如图2).
(1)若是四边形对角线的交点,求证:平面;
(2)若二面角是直二面角,求点到平面的距离.
7. (2023·重庆长寿)如图,四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,,E、F分别是PC、AD中点.
(1)求直线DE和PF夹角的余弦值;
(2)求点E到平面PBF的距离.
8.(2022·河北唐山)如图,已知长方体==1,直线BD与平面所成的角为30°,AE垂直BD于E,F为的中点.
(1)求异面直线AE与BF所成的角的余弦;
(2)求点A到平面BDF的距离.
题组三 线线距
1. (2023·全国·课时练习)如图,多面体是由长方体一分为二得到的,,,,点D是中点,则异面直线与的距离是______.
2. (2023·福建)如图,在正方体中,AB=1,M,N分别是棱AB,的中点,E是BD的中点,则异面直线,EN间的距离为______.
3. (2023·浙江)如图,正四棱锥的棱长均为2,点E为侧棱PD的中点.若点M,N分别为直线AB,CE上的动点,则MN的最小值为______.
4. (2023·湖北)如图,棱长为1的正方体ABCD-A1B1C1D1中,N是棱AD的中点,M是棱CC1上的点,且CC1=3CM,则直线BM与B1N之间的距离为____.
题组四 线面距
1. (2023·重庆一中)如图,在正三棱柱中,已知,D为的中点,E在上.
(1)若,证明:DE⊥CE;
(2)若平面CDE,求直线和平面CDE的距离.
2. (2023·河南)如图,长方体的棱长DA、DC和的长分别为1、2、1.求:
(1)顶点B到平面的距离;
(2)直线到平面的距离.
3. (2023·北京市)如图,在四棱锥中,底面为正方形,平面平面,,,在棱上取点,使得平面.
(1)求证:为中点;
(2)求平面与平面夹角的余弦值;
(3)求直线到平面的距离.
题组五 面面距
1. (2023·河北)正方体的棱长为,则平面与平面的距离为_______.
2. (2023·全国·高二专题练习)直四棱柱中,底面为正方形,边长为,侧棱,分别为的中点,分别是的中点.
(1)求证:平面平面;
(2)求平面与平面的距离.
3. (2023·湖南)在棱长为的正方体中,、分别是、的中点,求平面与平面之间的距离.
4. (2023·湖南)在正方体中,M,N,E,F分别为,,,的中点,棱长为4,求平面MNA与平面EFBD之间的距离.
5. (2023·湖南)如图,已知正方体的棱长为2,E,F,G分别为AB,BC,的中点.
(1)求证:平面平面EFG;
(2)求平面与平面EFG间的距离.
7.6 空间向量求空间距离(精练)(基础版)
题组一 点线距
1. (2023·湖南益阳)在棱长为1的正方体中,为的中点,则点到直线的距离为( )
A.B.1C.D.
【答案】B
【解析】建立如图所示的空间直角坐标系,
由已知,得,,,
,,
所以在上的投影为,
所以点到直线的距离为故选:B
2. (2023·山东)点是直线上一点,是直线的一个方向向量,则点到直线的距离是______.
【答案】
【解析】由题意,点和,可得,且,
所以点到直线的距离是.
故答案为:.
3. (2023云南)如图,已知三棱柱的棱长均为2,,.
(1)证明:平面平面ABC;
(2)设M为侧棱上的点,若平面与平面ABC夹角的余弦值为,求点M到直线距离.
【答案】(1)见解析(2)
【解析】(1)取AC的中点O,连接,,,所以由题设可知,为边长为2的等边三角形,所以,
由,,所以所以平面ABC;
平面,所以平面平面ABC;
(2)以OA所在直线为x轴,以OB所在直线为y轴,以所在直线为z轴,建立空间直角坐标系,
所以
设可得,
设平面的法向量为则
即取
所以因为为平面ABC的一个法向量,
设平面与平面ABC夹角为,
解得,所以
所以点M到直线距离
题组二 点面距
1. (2023·新疆)如图所示,在四棱锥中,平面,,在四边形中,,,,点在上,,与平面成的角.
(1)求证:平面;
(2)点到平面的距离.
【答案】(1)证明见解析;(2).
【解析】(1)以点为空间直角坐标系的坐标原点,为x轴,为y轴,为z轴建如图所示的空间直角坐标系,证明:∵平面,∴为与平面成的角,∴.∵,∴,,∴,,,,.∴,,.设平面的法向量为,由,即,可得,,∴.又,∴,又不在平面内,∴平面.
(2)取的中点,如图所示,则,,,∴.又,∴,即,又,平面,平面,∴平面,∴ 是平面的法向量,平面的单位法向量为,又,∴点到平面的距离为
2. (2023·重庆一中)已知四棱锥S-ABCD的底面是正方形,平面ABCD,求证:
(1)平面SAC;
(2)若,求点C到平面SBD的距离.
【答案】(1)证明见解析(2)
【解析】(1)证明:平面ABCD,平面ABCD,,又四边形ABCD为正方形,,又,平面;
(2)因为平面ABCD,平面ABCD,所以,因为,所以两两垂直,所以以A为坐标原点,AB、AD、AS分别为x、y、z轴建立空间直角坐标系则,所以,,设平面BDS的法向量为,则,令,则所以点C到平面SBD的距离
3. (2023·上海)如图,是矩形,平面,,,、分别是、的中点,求点到平面的距离.
【答案】
【解析】如图,以为原点建立空间直角坐标系,则、 、、、,
、分别是、的中点,,
设为平面的一个法向量,,,
即且,
令,得,
在上的射影长,即点到平面的距离.
4. (2023·北京)已知,分别是正方形边,的中点,交于,垂直于所在平面.
(1)求证:平面.
(2)若,,求点到平面的距离.
【答案】(1)证明见解析(2)
【解析】(1)证明:如图所示,连接交于,因为是正方形边,的中点,,所以,又因为垂直于所在平面,平面,所以,因为且平面,所以平面.
解:建立如图所示的空间直角坐标系,因为,,则,,,,可得,,设平面的法向量,则,令时,可得,所以又因为向量,则点到面的距离.
5.(2023·全国·高三专题练习)在如图所示的五面体中,面是边长为2的正方形,平面,,且,为的中点.
(1)求证:平面;
(2)求二面角的余弦值;
(3)求点到平面的距离.
【答案】(1)求证见解析(2)(3)
【解析】(1)证明:因为平面,平面,所以,因为,所以两两垂直,所以以为原点,所在的直线分别为轴建立空间直角坐标系,如图所示,因为面是边长为2的正方形,,且,为的中点,所以,,,,,,,所以,因为平面的法向量可以为,所以,即,又平面,所以平面;
(2)解:因为,,设平面的法向量为,则,令,则,所以,因为平面,,所以平面,因为平面,所以,因为,所以平面,所以平面的法向量可以为,设二面角为,由图可知二面角为钝角,则,所以二面角的余弦值为;
(3)解:由(2)知平面的法向量为,又,设点到平面的距离为,则所以点到平面的距离;
6. (2023·湖南·周南中学)某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍甍”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E、F、G分别是正方形的三边AB、CD、AD的中点,先沿着虚线段FG将等腰直角三角形FDG裁掉,再将剩下的五边形ABCFG沿着线段EF折起,连接AB、CG就得到了一个“刍甍”(如图2).
(1)若是四边形对角线的交点,求证:平面;
(2)若二面角是直二面角,求点到平面的距离.
【答案】(1)证明见解析(2)
【解析】(1)证明:取线段中点,连接、,
由图1可知,四边形EBCF是矩形,且,
∴O是线段BF与CE的中点,且,
在图1中知且,且,
所以在图2中,且,且,
∴四边形是平行四边形,则,
由于平面,平面,∴平面.
(2)由图1,,折起后在图2中仍有,,
∴即为二面角的平面角,∴,
以为坐标原点,分别为轴和轴正向建立空间直角坐标系,
则、、、、,
∴
设平面的一个法向量为
由,得,取,则
于是平面的一个法向量
点B到平面的距离为.
7. (2023·重庆长寿)如图,四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,,E、F分别是PC、AD中点.
(1)求直线DE和PF夹角的余弦值;
(2)求点E到平面PBF的距离.
【答案】(1);(2).
【解析】(1)因PD⊥平面ABCD,ABCD为正方形,则PD、DA、DC三线两两互相垂直,
如图,以点D为原点,DA为x轴,DC为y轴,DP为z轴建立空间直角坐标系D-xyz,
则,
则直线DE的方向向量,直线PF的方向向量,
,
所以直线DE和PF夹角的余弦值为.
(2)由(1)知,,,,
设平面PBF的法向量,则,令,得,
所以点E到平面PBF的距离为.
8.(2022·河北唐山)如图,已知长方体==1,直线BD与平面所成的角为30°,AE垂直BD于E,F为的中点.
(1)求异面直线AE与BF所成的角的余弦;
(2)求点A到平面BDF的距离.
【答案】(1)(2)
【解析】(1)在长方体中,以AB所在直线为x轴,AD所在直线为y轴,所在直线为z轴建立空间直角坐标系如图.
由已知AB==1,
可得A(0,0,0)、B(2,0,0)、F(1,0,1).
又AD⊥平面从而BD与平面所成的角即为∠DBA=30°,
又AB=2,AE⊥BD,AE=1,AD=
从而易得
∵==(-1,0,1).
设异面直线AE与BF所成的角为,
则.
即异面直线AE、BF所成的角的余弦为
(2)设=(x,y,z)是平面BDF的一个法向量.
=,=(-1,0,1),=(2,0,0).
由 ∴ ,即取=
所以点A到平面BDF的距离
题组三 线线距
1. (2023·全国·课时练习)如图,多面体是由长方体一分为二得到的,,,,点D是中点,则异面直线与的距离是______.
【答案】
【解析】以为坐标原点,分别以,,为轴,轴,轴建立空间直角坐标系,则,,,,
∴,,
设是,的公垂线方向上的单位向量,
则,即①,
,即②,
易知③,
联立解得,,或,,;
不妨取,
又∵,
则异面直线与的距离,
故答案为:.
2. (2023·福建)如图,在正方体中,AB=1,M,N分别是棱AB,的中点,E是BD的中点,则异面直线,EN间的距离为______.
【答案】
【解析】
以为原点,的方向为轴建立空间直角坐标系,易知,
,设同时垂直于,由,令,得,
又,则异面直线,EN间的距离为.
故答案为:.
3. (2023·浙江)如图,正四棱锥的棱长均为2,点E为侧棱PD的中点.若点M,N分别为直线AB,CE上的动点,则MN的最小值为______.
【答案】
【解析】
建立如图所示的空间直角坐标系,则有:
,,,,,
可得:
设,且
则有:,
可得:
则有:
故
则当且仅当时,
故答案为:
4. (2023·湖北)如图,棱长为1的正方体ABCD-A1B1C1D1中,N是棱AD的中点,M是棱CC1上的点,且CC1=3CM,则直线BM与B1N之间的距离为____.
【答案】
【解析】正方体的棱长为1,如图,以D为坐标原点,所在方向分别为轴正方向建立空间直角坐标系,
则B(1,1,0),B1(1,1,1),,,∴=(0,0,1),,.
设直线BM与B1N的公垂线方向上的向量,由,,
得,令x=2,则z=6,y=-7,∴,
设直线BM与B1N之间的距离为d,则d===.
故答案为:.
题组四 线面距
1. (2023·重庆一中)如图,在正三棱柱中,已知,D为的中点,E在上.
(1)若,证明:DE⊥CE;
(2)若平面CDE,求直线和平面CDE的距离.
【答案】(1)证明见解析(2)
【解析】(1)证明:因为,,
由余弦定理,
所以,
又因为平面,平面,
所以,
由于,
故DE⊥平面,
而平面,
故DE⊥EC;
(2)以C为坐标原点,CA为x轴,建立如图所示的空间直角坐标系.
此时,,,,,
设,
此时,,
设平面CDE的一个法向量为,
则,即
,
因为平面CDE,
所以,
故,
即,
解得,
故
由于平面CDE,直线和平面CDE的距离等于点和平面CDE的距离.
此时,,
取,
所以点和平面CDE的距离,
所以直线和平面CDE的距离为.
2. (2023·河南)如图,长方体的棱长DA、DC和的长分别为1、2、1.求:
(1)顶点B到平面的距离;
(2)直线到平面的距离.
【答案】(1)(2)
【解析】(1)以点D为原点,分别以、与为x、y、z轴的正方向,建立空间直角坐标系.则,,,,,,,.
设平面的法向量为,所以,.因为,,由,得,不妨取,则.
而向量,
所以B到平面的距离;
(2)直线到平面的距离等于到平面的距离.
因为,
所以到平面的距离.
3. (2023·北京市)如图,在四棱锥中,底面为正方形,平面平面,,,在棱上取点,使得平面.
(1)求证:为中点;
(2)求平面与平面夹角的余弦值;
(3)求直线到平面的距离.
【答案】(1)证明见解析(2)(3)
【解析】(1)连接,交于点,则平面平面,
又因为平面,平面,则,
由于底面为正方形,所以点为的中点,
因此可得为中点.
(2)由(1)知是的中点.
由于平面,所以,
故两两垂直,以为原点建立空间直角坐标系,如图所示,
,
设平面的法向量为,
所以,故可设,
平面的法向量为,
平面与平面夹角为,
则.
(3)
由于平面,则到平面的距离,即到平面的距离.
,
到平面的距离为.
即直线到平面的距离为.
题组五 面面距
1. (2023·河北)正方体的棱长为,则平面与平面的距离为_______.
【答案】
【解析】由题意,建立如图所示的空间直角坐标系,
则,
可得,
设平面的法向量为,则,
令,可得,所以,
因为,
所以,且,
所以平面平面,
所以平面与平面的距离等于点到平面的距离,
又因为,所以.
故答案为:.
2. (2023·全国·高二专题练习)直四棱柱中,底面为正方形,边长为,侧棱,分别为的中点,分别是的中点.
(1)求证:平面平面;
(2)求平面与平面的距离.
【答案】(1)证明见解析(2)
【解析】(1)法一:证明:连接分别为的中点,
分别是的中点,
,平面,平面,
平面,平行且等于,
是平行四边形,,
平面,平面,平面,
,平面平面;
法二: 如图所示,建立空间直角坐标系,
则,
,
,
,,,
平面,平面,平面,
平面,平面,平面,
又,平面平面,
(2)
法一:平面与平面的距离到平面的距离.
中,,,,
由等体积可得,.
法二:
设平面的一个法向量为,
则,则可取,
,
平面与平面的距离为
3. (2023·湖南)在棱长为的正方体中,、分别是、的中点,求平面与平面之间的距离.
【答案】
【解析】以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,
则、、、、、,
,,则,
因为、不在同一条直线上,则,
平面,平面,则平面,
同理可证平面,,故平面平面,
设平面的法向量为,,,
由,取,可得,
又因为,因此,平面与平面之间的距离为.
4. (2023·湖南)在正方体中,M,N,E,F分别为,,,的中点,棱长为4,求平面MNA与平面EFBD之间的距离.
【答案】.
【解析】以为轴建立空间直角坐标系,如图,
则,,,
,
设平面的一个法向量是,
则,取得,
又,
,
所以平面MNA与平面EFBD之间的距离.
5. (2023·湖南)如图,已知正方体的棱长为2,E,F,G分别为AB,BC,的中点.
(1)求证:平面平面EFG;
(2)求平面与平面EFG间的距离.
【答案】(1)证明见详解;(2)﹒
【解析】(1)∵E是AB中点,F是BC中点,
∴连接AC得,EF∥AC,
∵是平行四边形,
∴,
又平面平面,
∥平面,
同理,连接可得,可得EG∥平面,
与平面EFG,
∴平面∥平面EFG﹒
(2)如图:
以D为原点,DA、DC、分别为x轴、y轴、z轴,建立空间直角坐标系Oxyz﹒
则
∴,
设平面的法向量为,
则,取,
则平面与平面EFG间的距离为
相关试卷
这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.4 求和方法(精练)(基础版)(原卷版+解析版),共34页。
这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.3 利用递推公式求通项(精练)(基础版)(原卷版+解析版),共16页。
这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.2 等比数列(精练)(基础版)(原卷版+解析版),共27页。








