2024年新高考专用数学第一轮复习讲义一隅三反基础版 2.2 基本不等式（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 2.2 基本不等式（精讲）（基础版）（原卷版+解析版），共15页。试卷主要包含了常数替代型，配凑型，消元型，求参范围等内容，欢迎下载使用。

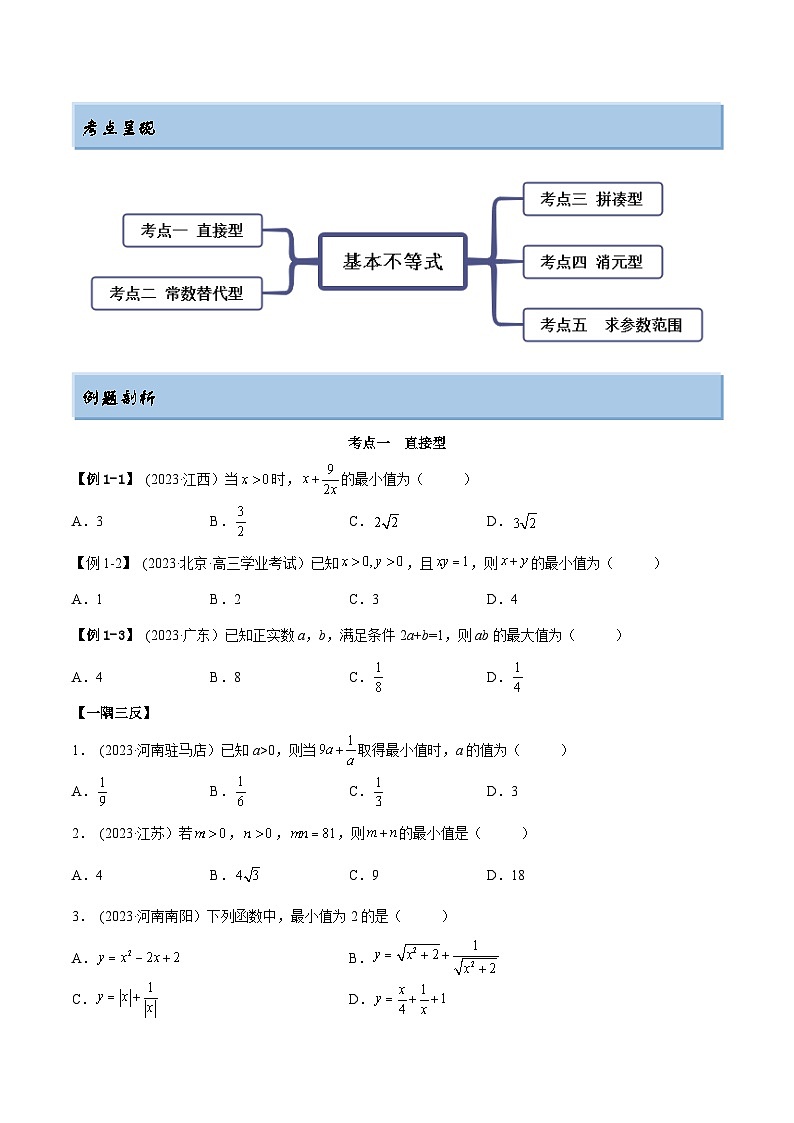
考点呈现
例题剖析
考点一 直接型
【例1-1】 (2023·江西）当时，的最小值为（ ）
A．3B．C．D．
【例1-2】 (2023·北京·高三学业考试）已知，且，则的最小值为（ ）
A．1B．2C．3D．4
【例1-3】 (2023·广东）已知正实数a，b，满足条件2a+b=1，则ab的最大值为（ ）
A．4B．8C．D．
【一隅三反】
1． (2023·河南驻马店）已知a>0，则当取得最小值时，a的值为（ ）
A．B．C．D．3
2． (2023·江苏）若，，，则的最小值是（ ）
A．4B．C．9D．18
3． (2023·河南南阳）下列函数中，最小值为2的是（ ）
A．B．
C．D．
考点二 常数替代型
【例2-1】 (2023·甘肃武威·高二期末（理））已知，，则的最小值为（ ）
A．B．C．D．
【例2-2】 (2023·湖南·长沙一中高三阶段练习）已知p，q为正实数且，则的最小值为（ ）
A．B．C．D．
【一隅三反】
1． (2023·河南郑州）已知实数a>0，b>0，，则的最小值为（ ）
A．B．C．D．
2． (2023·山西太原）已知为正实数，，则的最小值为（ ）
A．B．C．D．4
3． (2023·全国·高三专题练习）已知，，且，则的最小值为（ ）
A．B．C．D．
4． (2023·重庆巴蜀中学高三阶段练习）已知正实数a，b满足，则的最小值是（ ）
A．2B．C．D．6
考点三 配凑型
【例3-1】 (2023·全国·高三专题练习）函数的最小值是（ ）
A．B．
C．D．
【例3-2】 (2023·辽宁）已知正实数x，则的最大值是（ ）
A．B．C．D．
【例3-3】 (2023·河北邢台）若，则的最大值是（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习（理））若 ，则有（ ）
A．最大值B．最小值C．最大值D．最小值
2． (2023·山西·怀仁市第一中学校二模）函数的最小值为（ ）
A．8B．7C．6D．5
3． (2023·江苏徐州）设，为正数，且，则的最小值为（ ）
A．B．C．D．
考点四 消元型
【例4】 (2023·重庆·西南大学附中）已知正实数，满足，则的最大值为______.
【一隅三反】
1． (2023·北京·人大附中高三阶段练习）已知正数、满足，则的最小值是___________.
2． (2023·江苏·高考真题）已知，则的最小值是_______．
3． (2023·安徽·泾县中学高一阶段练习）设正实数、、满足，则的最大值为（ ）
A．B．C．D．
考点五 求参范围
【例5】 (2023·全国·高三专题练习）若对任意恒成立，则实数a的取值范围是（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习）当时，不等式恒成立，则实数的取值范围是（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）若对任意，恒成立，则实数a的取值范围是（ ）
A．B．
C．D．
3． (2023·全国·高三专题练习）若，且恒成立，则实数的取值范围是（ ）
A．B．C．D．
2.2 基本不等式（精讲）（基础版）
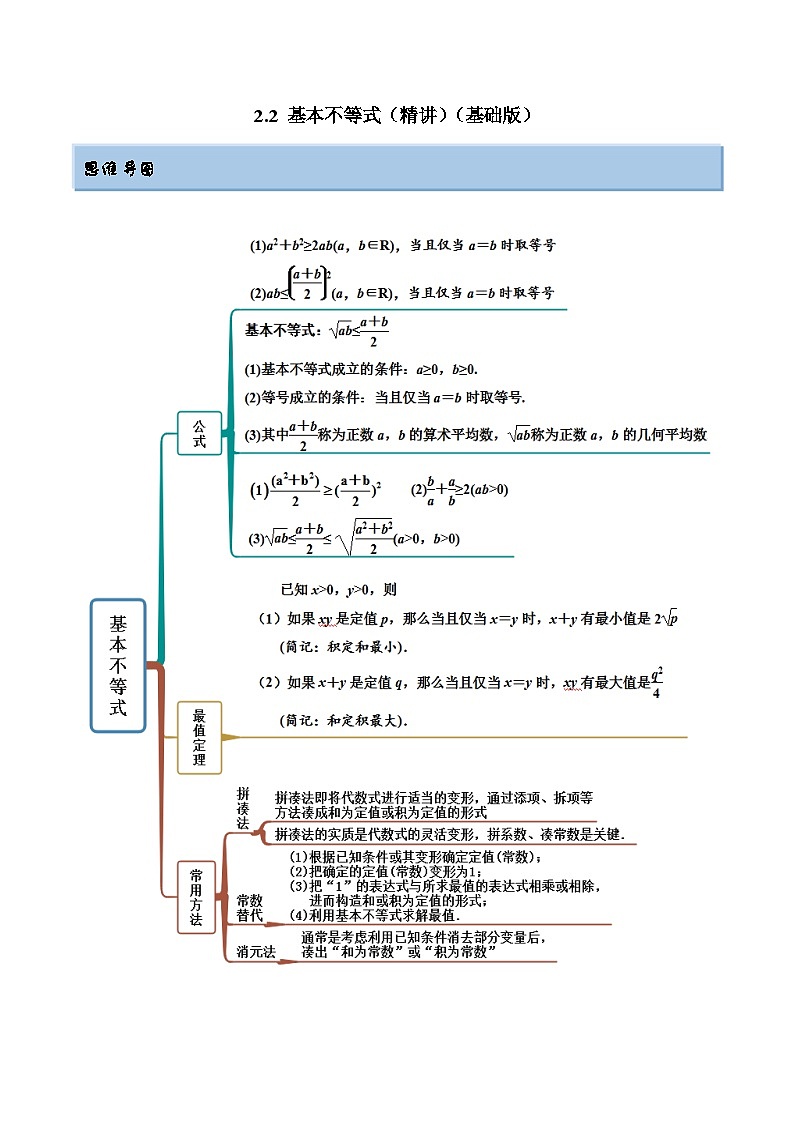
思维导图
考点呈现
例题剖析
考点一 直接型
【例1-1】 (2023·江西）当时，的最小值为（ ）
A．3B．C．D．
【答案】D
【解析】由（当且仅当时等号成立．）可得当时，的最小值为
故选：D
【例1-2】 (2023·北京·高三学业考试）已知，且，则的最小值为（ ）
A．1B．2C．3D．4
【答案】B
【解析】因为，所以，当且仅当时取“=”.故选：B.
【例1-3】 (2023·广东）已知正实数a，b，满足条件2a+b=1，则ab的最大值为（ ）
A．4B．8C．D．
【答案】C
【解析】因为正实数a，b，满足2a+b=1，所以，
当且仅当，即时，等号成立，所以ab的最大值为.故选：C
【一隅三反】
1． (2023·河南驻马店）已知a>0，则当取得最小值时，a的值为（ ）
A．B．C．D．3
【答案】C
【解析】∵a>0，∴，当且仅当，即时，等号成立，故选：C
2． (2023·江苏）若，，，则的最小值是（ ）
A．4B．C．9D．18
【答案】D
【解析】因为，，，所以，当且仅当时取等号，故选：D
3． (2023·河南南阳）下列函数中，最小值为2的是（ ）
A．B．
C．D．
【答案】C
【解析】，A不符合题意.
，当且仅当，即时，等号成立，显然不可能成立，B不符合题意.
，当且仅当，即时，等号成立，C符合题意.
当时，，D不符合题意.故选：C
考点二 常数替代型
【例2-1】 (2023·甘肃武威·高二期末（理））已知，，则的最小值为（ ）
A．B．C．D．
【答案】D
【解析】因为，，所以（当且仅当，即时取等号），即的最小值为4.故选：D.
【例2-2】 (2023·湖南·长沙一中高三阶段练习）已知p，q为正实数且，则的最小值为（ ）
A．B．C．D．
【答案】A
【解析】由可知，
，当，即时，“”成立，故选：A.
【一隅三反】
1． (2023·河南郑州）已知实数a>0，b>0，，则的最小值为（ ）
A．B．C．D．
【答案】B
【解析】依题意，，.
当且仅当时等号成立.故选：B
2． (2023·山西太原）已知为正实数，，则的最小值为（ ）
A．B．C．D．4
【答案】A
【解析】因为所以
当且仅当，即时等号成立故选：A
3． (2023·全国·高三专题练习）已知，，且，则的最小值为（ ）
A．B．C．D．
【答案】A
【解析】由题可知，乘“”得，当且仅当时，取等号，则的最小值为.故选：A
4． (2023·重庆巴蜀中学高三阶段练习）已知正实数a，b满足，则的最小值是（ ）
A．2B．C．D．6
【答案】B
【解析】由，得，
所以，
当且仅当，即取等号.故选：B.
考点三 配凑型
【例3-1】 (2023·全国·高三专题练习）函数的最小值是（ ）
A．B．
C．D．
【答案】D
【解析】因为，所以，当且仅当，即时等号成立.所以函数的最小值是.故选：D.
【例3-2】 (2023·辽宁）已知正实数x，则的最大值是（ ）
A．B．C．D．
【答案】D
【解析】因为，又因为，所以，
所以，当且仅当时，即时等号成立，
所以，即y的最大值是.故选：D.
【例3-3】 (2023·河北邢台）若，则的最大值是（ ）
A．B．C．D．
【答案】B
【解析】因为，所以
，
当且仅当，即时，等号成立，故选：B.
【一隅三反】
1． (2023·全国·高三专题练习（理））若 ，则有（ ）
A．最大值B．最小值C．最大值D．最小值
【答案】A
【解析】因，则，
于是得，当且仅当，即时取“=”，所以当时，有最大值.故选：A
2． (2023·山西·怀仁市第一中学校二模）函数的最小值为（ ）
A．8B．7C．6D．5
【答案】D
【解析】因为，所以3x－1>0，所以，
当且仅当，即x =1时等号成立，故函数的最小值为5．选：D．
3． (2023·江苏徐州）设，为正数，且，则的最小值为（ ）
A．B．C．D．
【答案】B
【解析】∵，∴，即，
∴
，当且仅当，且时，即，时等号成立.
故选：.
考点四 消元型
【例4】 (2023·重庆·西南大学附中）已知正实数，满足，则的最大值为______.
【答案】
【解析】依题意正实数，满足，，，当且仅当，时等号成立.
故答案为：
【一隅三反】
1． (2023·北京·人大附中高三阶段练习）已知正数、满足，则的最小值是___________.
【答案】
【解析】因为、为正数，由基本不等式可得，所以，，
当且仅当时，即当时，等号成立，故的最小值为.故答案为：.
2． (2023·江苏·高考真题）已知，则的最小值是_______．
【答案】
【解析】∵∴且
∴，当且仅当，即时取等号.
∴的最小值为.故答案为：.
3． (2023·安徽·泾县中学高一阶段练习）设正实数、、满足，则的最大值为（ ）
A．B．C．D．
【答案】C
【解析】因为正实数、、满足，则，
则，当且仅当时取等号.
故的最大值为.故选：C.
考点五 求参范围
【例5】 (2023·全国·高三专题练习）若对任意恒成立，则实数a的取值范围是（ ）
A．B．C．D．
【答案】C
【解析】因为，所以，当且仅当即时取等号，因为恒成立，所以，即；故选：C
【一隅三反】
1． (2023·全国·高三专题练习）当时，不等式恒成立，则实数的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】当时，（当且仅当时取等号），，即的取值范围为.故选：D.
2． (2023·全国·高三专题练习）若对任意，恒成立，则实数a的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】由题意，对任意，则有，
当且仅当时，即时，等号成立，即的最大值为，
又由对任意时，恒成立，所以，即的取值范围为.故选：A.
3． (2023·全国·高三专题练习）若，且恒成立，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】不等式恒成立，即，
，
等号成立的条件是，即，与条件联立，解得 ，
所以的最小值是8，即，解得：.故选：A