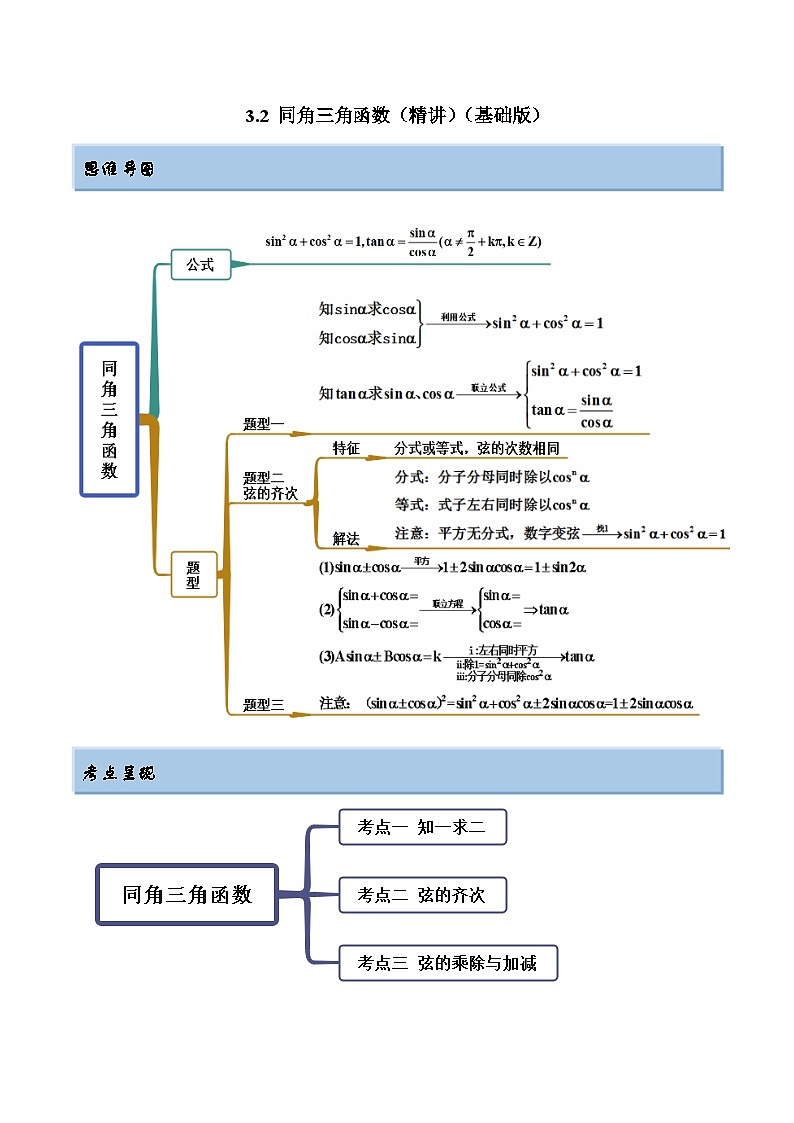
2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.2 同角三角函数（精讲）（基础版）（原卷版+解析版）

这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 3.2 同角三角函数（精讲）（基础版）（原卷版+解析版），共14页。试卷主要包含了知一求二，弦的齐次，弦的乘除与加减等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 知一求二
【例1-1】 (2023·广东）已知是第三象限角，且，则（ ）
A．B．C．D．
【例1-2】 (2023·宁夏·固原一中一模）若，且在第四象限，则（ ）
A．B．C．D．
【例1-3】 (2023·青海西宁）已知角的终边经过点，且，则（ ）
A．B．C．D．
sin α，cs α，tan α的知一求二问题
(1)利用sin2α＋cs2α＝1可实现α的正弦、余弦的互化，利用eq \f(sin α,cs α)＝tan α可以实现角α的弦切互化．
(2)由一个角的任意一个三角函数值可求出这个角的另外两个三角函数值，因为利用“平方关系”公式，需求平方根，会出现两解，需根据角所在的象限判断符号，当角所在的象限不明确时，要进行分类讨论．
温馨提示
【一隅三反】
1． (2023·广东·深圳外国语学校高三阶段练习）已知角，，则（ ）
A．B．C．D．
2． (2023·浙江省杭州第二中学）已知，则“ ”是“ ”的 （ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
3． (2023·北京市第三十五中学高三期中）已知，且，那么（ ）
A．B．C．D．
考点二 弦的齐次
【例2-1】 (2023·全国·模拟预测（理））已知，则的值为（ ）
A．1B．C．2D．5
【例2-2】 (2023·内蒙古包头·高三期末）若，则（ ）
A．B．C．D．
【例2-3】 (2023·全国·模拟预测（文））已知在处的切线倾斜角为，则的值为（ ）
A．7B．C．5D．-3
【例2-4】 (2023·全国·高考真题）若，则（ ）
A．B．C．D．
若已知正切值，求一个关于正弦和余弦的齐次分式的值，则可以通过分子、分母同时除以一个余弦的齐次幂将其转化为一个关于正切的分式，代入正切值就可以求出这个分式的值，对于分母为1的二次式，可用sin2α＋cs2α做分母求解．
温馨提示
【一隅三反】
1．（2011·全国·高考真题（理））已知角的顶点与原点重合，始边与轴的正半轴重合，终边在直线上，则（ ）
A．B．C．D．
2． (2023·湖南益阳·一模）若，则
A．B．C．D．
3． (2023·河南新乡·二模（文））已知是第三象限角，且，则（ ）
A．B．C．D．
4． (2023·全国·模拟预测（理））已知，则（ ）
A．B．C．D．
5． (2023·云南昭通·高三阶段练习（文））已知向量，且，则的值为（ ）
A．B．C．D．
6． (2023·江苏·苏州中学高三开学考试）已知，且，则（ ）
A．5或B．5或C．5D．
7． (2023·内蒙古包头·高三期末（理））若，则（ ）
A．B．C．D．
考点三 弦的乘除与加减
【例3-1】 (2023·西藏·拉萨中学高三阶段练习（理））已知，则（ ）
A．B．C．D．
【例3-2】 (2023·全国·高三专题练习）已知，则的值等于（ ）
A．B．C．D．
【例3-3】 (2023·全国·高三专题练习）已知，则（ ）
A．B．C．或D．或
【一隅三反】
1． (2023·山东聊城·高三期末）已知，且，则的值为________.
2． (2023·陕西·西安中学三模（文））已知，且，则___.
3． (2023·广东肇庆·二模）若，则______．
4． (2023·全国·高三专题练习）已知，若是第二象限角，则的值为__________.
5． (2023·全国·高三专题练习）函数y＝sinx－csx＋sinxcsx的值域为________.
6． (2023·江苏·高三专题练习）已知sinθ＋csθ＝，θ∈(0，π)，则tanθ＝________.
3.2 同角三角函数（精讲）（基础版）
思维导图
考点呈现
例题剖析
考点一 知一求二
【例1-1】 (2023·广东）已知是第三象限角，且，则（ ）
A．B．C．D．
【答案】A
【解析】因为是第三象限角，且，所以，故选：A.
【例1-2】 (2023·宁夏·固原一中一模）若，且在第四象限，则（ ）
A．B．C．D．
【答案】D
【解析】∵，且在第四象限，∴，∴．故选：D．
【例1-3】 (2023·青海西宁）已知角的终边经过点，且，则（ ）
A．B．C．D．
【答案】B
【解析】点的纵坐标为，且，所以在第三象限，所以，
，.故选：B
sin α，cs α，tan α的知一求二问题
(1)利用sin2α＋cs2α＝1可实现α的正弦、余弦的互化，利用eq \f(sin α,cs α)＝tan α可以实现角α的弦切互化．
(2)由一个角的任意一个三角函数值可求出这个角的另外两个三角函数值，因为利用“平方关系”公式，需求平方根，会出现两解，需根据角所在的象限判断符号，当角所在的象限不明确时，要进行分类讨论．
温馨提示
【一隅三反】
1． (2023·广东·深圳外国语学校高三阶段练习）已知角，，则（ ）
A．B．C．D．
【答案】B
【解析】因为，所以，所以，.故选：B
2． (2023·浙江省杭州第二中学）已知，则“ ”是“ ”的 （ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】B
【解析】因为，所以当，x可以是锐角也可以时钝角，所以，所以不满足充分性；
当时，x必为锐角，所以成立，必要性满足故选：B
3． (2023·北京市第三十五中学高三期中）已知，且，那么（ ）
A．B．C．D．
【答案】D
【解析】由题意得：，故选：D
考点二 弦的齐次
【例2-1】 (2023·全国·模拟预测（理））已知，则的值为（ ）
A．1B．C．2D．5
【答案】A
【解析】由题意得：，故选：A．
【例2-2】 (2023·内蒙古包头·高三期末）若，则（ ）
A．B．C．D．
【答案】A
【解析】故选：A.
【例2-3】 (2023·全国·模拟预测（文））已知在处的切线倾斜角为，则的值为（ ）
A．7B．C．5D．-3
【答案】B
【解析】因为，所以，所以
.故选：B
【例2-4】 (2023·全国·高考真题）若，则（ ）
A．B．C．D．
【答案】C
【解析】将式子进行齐次化处理得：
．故选：C．
若已知正切值，求一个关于正弦和余弦的齐次分式的值，则可以通过分子、分母同时除以一个余弦的齐次幂将其转化为一个关于正切的分式，代入正切值就可以求出这个分式的值，对于分母为1的二次式，可用sin2α＋cs2α做分母求解．
温馨提示
【一隅三反】
1．（2011·全国·高考真题（理））已知角的顶点与原点重合，始边与轴的正半轴重合，终边在直线上，则（ ）
A．B．C．D．
【答案】B
【解析】由已知条件可知，点在直线上，则，，
所以，.故选：B.
2． (2023·湖南益阳·一模）若，则
A．B．C．D．
【答案】C
【解析】由可知：∴，∴，
又==.故选C.
3． (2023·河南新乡·二模（文））已知是第三象限角，且，则（ ）
A．B．C．D．
【答案】C
【解析】由题可知，，且是第三象限角，则，，所以,
故选：C.
4． (2023·全国·模拟预测（理））已知，则（ ）
A．B．C．D．
【答案】D
【解析】由，得，．
故选：D．
5． (2023·云南昭通·高三阶段练习（文））已知向量，且，则的值为（ ）
A．B．C．D．
【答案】A
【解析】由题意可得，
即.故选：A.
6． (2023·江苏·苏州中学高三开学考试）已知，且，则（ ）
A．5或B．5或C．5D．
【答案】C
【解析】∵ ，∴ ，即，又
∴ ，∴ ，故选：C.
7． (2023·内蒙古包头·高三期末（理））若，则（ ）
A．B．C．D．
【答案】A
【解析】
.故选：A.
考点三 弦的乘除与加减
【例3-1】 (2023·西藏·拉萨中学高三阶段练习（理））已知，则（ ）
A．B．C．D．
【答案】B
【解析】因为，所以两边平方得，
又因为，所以，即，
所以.故选：B
【例3-2】 (2023·全国·高三专题练习）已知，则的值等于（ ）
A．B．C．D．
【答案】A
【解析】，，，，
，即.故选：A
【例3-3】 (2023·全国·高三专题练习）已知，则（ ）
A．B．C．或D．或
【答案】B
【解析】因为，①所以两边平方可得，
则，所以是钝角，则，
所以，②，
联立①②可得，则．故选:B．
【一隅三反】
1． (2023·山东聊城·高三期末）已知，且，则的值为________.
【答案】
【解析】
，，
又，所以，所以，，
故答案为：
2． (2023·陕西·西安中学三模（文））已知，且，则___.
【答案】
【解析】因为，所以，
因此有：，
把代入，得，故答案为：
3． (2023·广东肇庆·二模）若，则______．
【答案】
【解析】∵，∴，所以．
故答案为：.
4． (2023·全国·高三专题练习）已知，若是第二象限角，则的值为__________.
【答案】
【解析】，
所以，所以，
所以.又因为是第二象限角，所以，，所以.
故答案为：.
5． (2023·全国·高三专题练习）函数y＝sinx－csx＋sinxcsx的值域为________.
【答案】
【解析】设t＝sinx－csx，则t2＝sin2x＋cs2x－2sinx·csx，sinxcsx＝，
，∴.∴y＝－＋t＋＝－ (t－1)2＋1，t∈[－，].
当t＝1时，ymax＝1；当t＝－时，ymin＝.∴函数的值域为.
6． (2023·江苏·高三专题练习）已知sinθ＋csθ＝，θ∈(0，π)，则tanθ＝________.
【答案】
【解析】将已知等式①
两边平方得：，，
，，，即，，
②，联立①②，解得：，，
则．故答案为：．