

- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.2 利用导数求单调性(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.3 利用导数求极值最值(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.4 构造函数常见方法(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.4 构造函数常见方法(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.5 导数的综合运用(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 4.3 利用导数求极值最值(精练)(提升版)(原卷版+解析版)
展开A.1个B.2个C.3个D.4个
2. (2023·天津实验中学)下列函数中存在极值点的是( )
A.B.
C.D.
3. (2023·福建省连城县第一中学)函数的极值点的个数是( )
A.B.C.D.无数个
4. (2023·全国·哈师大附中)已知是函数的一个极值点,则的值是( )
A.1B.C.D.
5. (2023·辽宁·鞍山市华育高级中学)已知函数的导函数的图像如图所示,则下列判断正确的是( )
A.在区间上,是增函数B.在区间上,是减函数
C.为的极小值点D.2为的极大值点
6. (2023·湖北·南漳县第一中学)函数的极大值为( )
A.-2B.2C.D.不存在
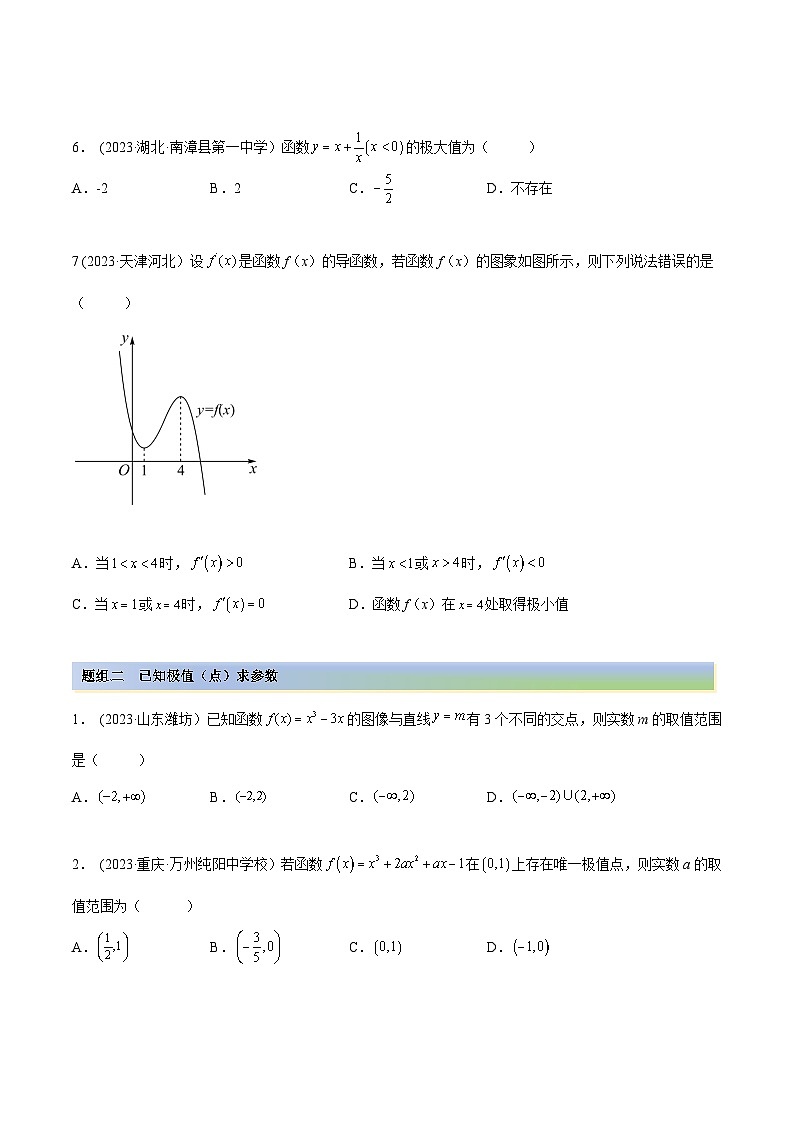
7 (2023·天津河北)设是函数f(x)的导函数,若函数f(x)的图象如图所示,则下列说法错误的是( )
A.当时,B.当或时,
C.当或时,D.函数f(x)在处取得极小值
题组二 已知极值(点)求参数
1. (2023·山东潍坊)已知函数的图像与直线有3个不同的交点,则实数m的取值范围是( )
A.B.C.D.
2. (2023·重庆·万州纯阳中学校)若函数在上存在唯一极值点,则实数a的取值范围为( )
A.B.C.D.
3. (2023·四川省成都市新都一中)已知没有极值,则实数的取值范围为( )
A.B.
C.D.
4. (2023·湖北)函数在内存在极值点,则( )
A.B.C.或D.或
5. (2023·河南)已知函数有两个极值点,则实数的取值范围是( )
A.B.
C.D.
6. (2023·安徽·蒙城第一中学)已知为常数,函数有两个极值点,其中一个极值点满足,则的取值范围是( )
A.B.C.D.
7 (2023·陕西·长安一中)已知在中,三个内角,,的对边分别为,,,若函数无极值点,则角B的最大值是( )
A.B.C.D.
8. (2023·四川·绵阳中学实验学校)若函数在处有极值10,则( )
A.6B.C.或15D.6或
9. (2023·青海·大通回族土族自治县教学研究室二模(理))设函数,则下列不是函数极大值点的是( )
A.B.C.D.
10. (2023·全国·高三专题练习)已知t和是函数的零点,且也是函数的极小值点,则的极大值为( )
A.1B.4C.D.
11. (2023·广西·高三阶段练习(理))已知函数在其定义域的一个子区间上有极值,则实数a的取值范围是( )
A.B.C.D.
12. (2023·安徽·合肥市第八中学)已知函数在处取极小值,且的极大值为4,则( )
A.-1B.2C.-3D.4
13. (2023·河北承德)已知是函数的极值点,则的极大值为_____.
14. (2023·北京·101中学)设是函数的两个极值点,若,则实数a的取值范围是______.
15. (2023·浙江宁波)已知函数,若是函数的唯一极值点,则实数k的取值范围是_______.
题组三 无参函数的最值
1. (2023·海南华侨中学)已知函数,下列说法正确的是( )
A.函数在上递增B.函数无极小值
C.函数只有一个极大值D.函数在上最大值为3
2. (2023·湖北·模拟预测),的最小值为___________.
3. (2023·江苏·南京市江宁高级中学模拟预测)若函数在内有且只有一个零点,则在上的最大值与最小值的和为_______.
4. (2023·全国·高三专题练习)若实数a、b、c、d满足,则的最小值为______.
5. (2023·四川省成都市新都一中)函数在区间上的最大值为______.
6. (2023·天津实验中学)函数在区间上的最小值为__________.
7. (2023·四川·威远中学校)对任意,存在,使得,则的最小值为_____.
8. (2023·河南开封)已知是奇函数,当时,,则当时,的最小值为________.
题组四 已知最值求参数
1. (2023·江西萍乡·三模)已知定义在上的函数,对任意,当时,都有,若存在,使不等式成立,则实数的最大值为( )
A.B.C.D.
2. (2023·辽宁·鞍山市华育高级中学)已知,,若,则当取得最小值时,所在区间是( )
A.B.C.D.
3. (2023·河南·模拟预测(理))已知函数至多有2个不同的零点,则实数a的最大值为( ).
A.0B.1C.2D.e
4. (2023·辽宁·辽师大附中)设函数(n为正整数),则在[0,1]上的最大值为( )
A.0B.C.D.
5. (2023·河南安阳)已知函数,若时,在处取得最大值,则实数a的取值范围是( )
A.B.C.D.
6. (2023·江西)设两个实数a,b满足:,则正整数n的最大值为( ).(参考数据:)
A.7B.8C.9D.10
题组五 最值极值的综合运用
1. (2023·浙江·宁波市李惠利中学)(多选)对于函数,下列选项正确的是( )
A.函数极小值为,极大值为
B.函数单调递减区间为,单调递增区为
C.函数最小值为为,最大值
D.函数存在两个零点1和
2. (2023·福建泉州)(多选)函数在处取得极大值,则a的值可以是( )
A.-1B.0C.3D.4
3. (2023·黑龙江·哈尔滨市第六中学校)(多选)已知函数,下列命题正确的是( )
A.若是函数的极值点,则
B.若是函数的极值点,则在上的最小值为
C.若在上单调递减,则
D.若在上恒成立,则
4. (2023·河南·三模)已知函数.
(1)讨论极值点的个数;
(2)证明:.
5. (2023·湖南·临澧县第一中学二模)已知函数.
(1)当时,若在上存在最大值,求m的取值范围;
(2)讨论极值点的个数.
6. (2023·江西·上饶市第一中学模拟预测)已知函数.
(1)当时,求函数的极值;
(2)若函数在无零点,求实数a的取值范围.
7. (2023·北京市十一学校高三阶段练习)已知函数
(1)当时,求曲线在点处的切线方程;
(2)判断函数的极值点的个数,并说明理由.
8. (2023·四川省峨眉第二中学校)已知,函数.
(1)讨论的单调性;
(2)当时,若对恒成立,求实数b的最大值.
9 (2023·江苏·华罗庚中学三模)已知函数 ,(为自然对数的底数,).
(1)求函数的单调区间;
(2)若,,当时,,求的最小值.
10. (2023·天津市新华中学)已知函数,其中且
(1)当时,求函数的极值;
(2)求函数的单调区间;
(3)若存在,使函数,在处取得最小值,试求的最大值.
4.3 利用导数求极值最值(精练)(提升版)
题组一 无参函数的极值(点)
1. (2023·山东·巨野县实验中学)已知函数的定义域为,导函数在内的图像如图所示,则函数在内的极小值有( )
A.1个B.2个C.3个D.4个
【答案】A
【解析】由导函数在区间内的图像可知,
函数在内的图像与轴有四个公共点,
在从左到右第一个点处导数左正右负,在从左到右第二个点处导数左负右正,
在从左到右第三个点处导数左正右正,在从左到右第四个点处导数左正右负,
所以函数在开区间内的极小值有个,故选:A.
2. (2023·天津实验中学)下列函数中存在极值点的是( )
A.B.
C.D.
【答案】B
【解析】对选项A,,故没有极值点;
对选项B,,则极值点为,故正确;
对选项C,,故没有极值点;
对选项D,,故没有极值点;故选:B
3. (2023·福建省连城县第一中学)函数的极值点的个数是( )
A.B.C.D.无数个
【答案】A
【解析】由题,,故无极值点故选:A
4. (2023·全国·哈师大附中)已知是函数的一个极值点,则的值是( )
A.1B.C.D.
【答案】D
【解析】,
∴,∴,∴故选:D
5. (2023·辽宁·鞍山市华育高级中学)已知函数的导函数的图像如图所示,则下列判断正确的是( )
A.在区间上,是增函数B.在区间上,是减函数
C.为的极小值点D.2为的极大值点
【答案】D
【解析】由导函数的图像可知,
在区间上为单调递减,在区间上为单调递增,则选项不正确;
在区间上,,则是增函数,则选项不正确;
由图像可知,且为单调递增区间,为单调递减区间,则为的极大值点,则选项不正确;由图像可知,且为单调递增区间,为单调递减区间,则为的极大值点,则选项正确;故选:D.
6. (2023·湖北·南漳县第一中学)函数的极大值为( )
A.-2B.2C.D.不存在
【答案】A
【解析】=1-=.令得或(舍).
由于,当时,,当时,,
所以函数在上单调递增,在上单调递减.
故函数在处取得极大值.故选:A
7 (2023·天津河北)设是函数f(x)的导函数,若函数f(x)的图象如图所示,则下列说法错误的是( )
A.当时,B.当或时,
C.当或时,D.函数f(x)在处取得极小值
【答案】D
【解析】A.由图象知:当时,函数f(x)递增,所以,故正确;
B.由图象知:当或时,函数f(x)递增,所以,故正确;
C.由图象知:当或时,函数f(x)分别取得极小值和极大值,故正确;
D.由图象知:函数f(x)在处取得极大值,故错误;故选:D
题组二 已知极值(点)求参数
1. (2023·山东潍坊)已知函数的图像与直线有3个不同的交点,则实数m的取值范围是( )
A.B.C.D.
【答案】B
【解析】对函数求导得:,
当或时,,当时,,即在,上单调递增,在上单调递减,
在处取得极大值,在处取得极小值,
在同一坐标系内作出函数的图像和直线,如图,
观察图象知,当时,函数的图像与直线有3个不同的交点,
所以实数m的取值范围是.故选:B
2. (2023·重庆·万州纯阳中学校)若函数在上存在唯一极值点,则实数a的取值范围为( )
A.B.C.D.
【答案】B
【解析】由题意知:,若函数在上存在唯一极值点,
则,即,解得.故选:B.
3. (2023·四川省成都市新都一中)已知没有极值,则实数的取值范围为( )
A.B.
C.D.
【答案】C
【解析】;
在上没有极值,,即,
解得:,即实数的取值范围为.故选:C.
4. (2023·湖北)函数在内存在极值点,则( )
A.B.C.或D.或
【答案】A
【解析】由题意知:在内存在变号零点,即在内有解,则,易得在内单调递减,值域为,故.故选:A.
5. (2023·河南)已知函数有两个极值点,则实数的取值范围是( )
A.B.
C.D.
【答案】B
【解析】由题意有两个不等实根,,
设,,
当时,,递增,当时,,递减,
时,为极大值也是最大值,
时,,所以,
时, ,与轴只有一个交点,
所以当,即时,直线与的图象有两个交点,即有两个不等实根.
故选:B.
6. (2023·安徽·蒙城第一中学)已知为常数,函数有两个极值点,其中一个极值点满足,则的取值范围是( )
A.B.C.D.
【答案】D
【解析】,由函数有两个极值点,
则等价于有两个解,即与有两个交点,
所以.
直线过点
由在点处的切线为,显然直线过点
当时,直线与曲线交于不同两点(如下图),且,
,
令,则,
所以单调递增,,即,
故选: D.
7 (2023·陕西·长安一中)已知在中,三个内角,,的对边分别为,,,若函数无极值点,则角B的最大值是( )
A.B.C.D.
【答案】C
【解析】因为,所以,
若无极值点,即无变号零点,又二次函数开口向上,
所以恒成立,等价为判别式,即,得,
所以,因为,,所以的最大值为;故选:C.
8. (2023·四川·绵阳中学实验学校)若函数在处有极值10,则( )
A.6B.C.或15D.6或
【答案】B
【解析】 ,
又 时 有极值10
,解得 或
当 时,
此时 在 处无极值,不符合题意
经检验, 时满足题意 故选:B
9. (2023·青海·大通回族土族自治县教学研究室二模(理))设函数,则下列不是函数极大值点的是( )
A.B.C.D.
【答案】D
【解析】由题可得,
令,得或,,
则当时,,
当时,,
所以函数在,,上单调递增,在,,上单调递减,故不是函数极大值点的是.故选:D.
10. (2023·全国·高三专题练习)已知t和是函数的零点,且也是函数的极小值点,则的极大值为( )
A.1B.4C.D.
【答案】B
【解析】因函数在处取得极小值0,又t是函数的另一零点,因此函数只有两个零点,
从而有,求导得:,
当或时,,当时,,
于是,在处取得极小值,在处取得极大值,
所以的极大值为4.故选:B
11. (2023·广西·高三阶段练习(理))已知函数在其定义域的一个子区间上有极值,则实数a的取值范围是( )
A.B.C.D.
【答案】A
【解析】,令,即,解得,且,;,,∴在上单调递增,在上单调递减,
∴有极大值,∴,∴,故选:A.
12. (2023·安徽·合肥市第八中学)已知函数在处取极小值,且的极大值为4,则( )
A.-1B.2C.-3D.4
【答案】B
【解析】,所以
因为函数在处取极小值,所以,所以,,,
令,得或,当时,,所以在单调递增,当时,,所以在单调递增,当时,,所以在单调递增,所以在处有极大值为,解得,所以.故选:B
13. (2023·河北承德)已知是函数的极值点,则的极大值为_____.
【答案】0
【解析】因为,所以,得,
所以,所以当时,,单调递减,
当或时,,单调递增,所以是的极大值点,则.
故答案为:0
14. (2023·北京·101中学)设是函数的两个极值点,若,则实数a的取值范围是______.
【答案】
【解析】,
因为是函数的两个极值点,且,
所以是方一元二次方程的两个实根,且,
所以,即,解得.故答案为:
15. (2023·浙江宁波)已知函数,若是函数的唯一极值点,则实数k的取值范围是_______.
【答案】
【解析】的定义域为
是函数的唯一极值点
是导函数的唯一根
(Ⅰ)在无变号零点
令 ,则 ,即在上单调递增
此时
(Ⅱ)当 在有解 时,此时 ,解得
此时 在 和 上均单调递增,不符合题意
故答案为:
题组三 无参函数的最值
1. (2023·海南华侨中学)已知函数,下列说法正确的是( )
A.函数在上递增B.函数无极小值
C.函数只有一个极大值D.函数在上最大值为3
【答案】C
【解析】因为定义域为,
所以,
所以当或时,当时,
所以在上单调递减,在和上单调递增,
所以在处取得极大值,在处取得极小值,
即,,
又,,故函数在上最大值为;
故选:C
2. (2023·湖北·模拟预测),的最小值为___________.
【答案】3
【解析】令,则
当时,单调增,
当时,令,
时,递减
时,递增
∴
综上:
故答案为:3.
3. (2023·江苏·南京市江宁高级中学模拟预测)若函数在内有且只有一个零点,则在上的最大值与最小值的和为_______.
【答案】
【解析】当时,由可得,令,其中,
则,由,可得,列表如下:
如下图所示:
因为在内有且只有一个零点,则,
所以,,则,
当时,,此时函数单调递减,
当时,,此时函数单调递增,
则当时,,
又因为,,所以,,
因此,在上的最大值与最小值的和为.
故答案为:.
4. (2023·全国·高三专题练习)若实数a、b、c、d满足,则的最小值为______.
【答案】
【解析】∵,
∴点是曲线上的点,是直线上的点,
∴.
∵,
由得,;由得.
∴当时,取得极小值为1. 如图,
要使最小,当且仅当过曲线上的点且与线平行时.
∵,直线的斜率,∴,
∴或(由于,故舍去).∴.
设点到直线的距离为d,
则.
∵,∴的最小值为.
故答案为:.
5. (2023·四川省成都市新都一中)函数在区间上的最大值为______.
【答案】
【解析】对求导,可得:
故在区间上单调递减,在区间单调递增
可得:,,
可得:
故在区间上的最大值为
故答案为:
6. (2023·天津实验中学)函数在区间上的最小值为__________.
【答案】
【解析】因为,所以,
令,得,当时,,当时,,
所以当时,取得极小值,又,
所以在区间上的最小值为,故答案为:
7. (2023·四川·威远中学校)对任意,存在,使得,则的最小值为_____.
【答案】
【解析】由得:,令,则,;
,
令,则,令,则,
在上单调递增,又,
当时,;当时,;
在上单调递减,在上单调递增,,
即的最小值为.
故答案为:.
8. (2023·河南开封)已知是奇函数,当时,,则当时,的最小值为________.
【答案】1
【解析】,,所以,
又因为是奇函数,所以,
所以当,,,
令,所以,
则在上单调递减,在上单调递增,所以.
所以当时,的最小值为1.故答案为:1.
题组四 已知最值求参数
1. (2023·江西萍乡·三模)已知定义在上的函数,对任意,当时,都有,若存在,使不等式成立,则实数的最大值为( )
A.B.C.D.
【答案】B
【解析】因为对任意,当时,都有,所以在上单调递增,
则等价于,即,
令,,,
因为,所以,,所以,所以在上单调递减,
所以,即,所以的最大值为;故选:B
2. (2023·辽宁·鞍山市华育高级中学)已知,,若,则当取得最小值时,所在区间是( )
A.B.C.D.
【答案】D
【解析】令,即,∴,,∴,
令,则,
令,则,
∴在上单调递增,且,
∴存在唯一使得,
当时,, ,当时,, ,
∴,
即取得最小值时,,
由零点的存在定理验证的根的范围,
当时,,当时,,
故,
故选:.
3. (2023·河南·模拟预测(理))已知函数至多有2个不同的零点,则实数a的最大值为( ).
A.0B.1C.2D.e
【答案】C
【解析】令,得到,
函数至多有2个不同的零点,等价于至多有两个不同的根,
即函数与至多有2个不同的交点
令,
则,
当时,,单调递增,
当或时,,单调递减,
所以与为函数的极值点,且,
且在R上恒成立,
画出的图象如下:
有图可知:或时,符合题意,
其中,解得:
设,则,
当时,,当时,,
所以在上单调递增,在上单调递减,
由可得:,所以,综上:实数a的最大值为2故选:C
4. (2023·辽宁·辽师大附中)设函数(n为正整数),则在[0,1]上的最大值为( )
A.0B.C.D.
【答案】D
【解析】由,
令,可得或或,
在上,即递增;在上,即递减,
所以在[0,1]上的最大值为.故选:D
5. (2023·河南安阳)已知函数,若时,在处取得最大值,则实数a的取值范围是( )
A.B.C.D.
【答案】B
【解析】根据题意得当时恒成立
则,即
∴当时,在图像的下方
,则,则
故选:B.
6. (2023·江西)设两个实数a,b满足:,则正整数n的最大值为( ).(参考数据:)
A.7B.8C.9D.10
【答案】C
【解析】由题设且,令且,且,
所以,故时,时,
则上递增,上递减,即;
,故时,时,
则上递减,上递增,即;
综上,只需,整理得,取对数有,
所以时,不等式恒成立;
当时,,此时递增且,,
综上,,故n的最大值为9.
题组五 最值极值的综合运用
1. (2023·浙江·宁波市李惠利中学)(多选)对于函数,下列选项正确的是( )
A.函数极小值为,极大值为
B.函数单调递减区间为,单调递增区为
C.函数最小值为为,最大值
D.函数存在两个零点1和
【答案】AD
【解析】的定义域为,
所以,
所以为奇函数,
当时,,,
令,解得,
当时,,则为单调递增函数,
当时,,则为单调递减函数,
因为为奇函数,图象关于原点对称,
所以在上单调递减,在是单调递增,
所以的极小值为,极大值为,故A正确;
的单调递减区间为,单调递增区为,故B错误;
在无最值,故C错误;
令,解得,结合的单调性可得,存在两个零点1和,故D正确.
故选:AD
2. (2023·福建泉州)(多选)函数在处取得极大值,则a的值可以是( )
A.-1B.0C.3D.4
【答案】AB
【解析】,.
当时,令,,
,,单调递增,,,单调递减,则在处取得极大值;
当时,令,,.
当时,,,单调递增,在,,单调递减,则在处取得极大值;
当时,若,即时,在,,单调递增,,,单调递减,则在处取得极小值,不合题意,舍去;若,即时,恒成立,单调递增,不合题意,舍去;若,即时,在,,单调递增,,,单调递减,则在处取得极大值;综上所述:时,函数在处取得极大值.
故选:AB.
3. (2023·黑龙江·哈尔滨市第六中学校)(多选)已知函数,下列命题正确的是( )
A.若是函数的极值点,则
B.若是函数的极值点,则在上的最小值为
C.若在上单调递减,则
D.若在上恒成立,则
【答案】ABC
【解析】对于A,由,得,因为是函数的极值点,所以,得,经检验是函数的极小值点,所以A正确,
对于B,由选项A,可知,则,由,得或,由,得,所以在和递增,在上递减,所以当时,时,取得最小值,所以B正确,
对于C,因为在上单调递减,所以,即,得在上恒成立,令,则,所以在单调递增,所以,即,所以,所以C正确,
对于D,由在上恒成立,得 在上恒成立,即在上恒成立,令,,则,所以上单调递增,所以,所以,所以D错误,故选:ABC
4. (2023·河南·三模)已知函数.
(1)讨论极值点的个数;
(2)证明:.
【答案】(1)答案见解析;(2)证明见解析﹒
【解析】(1)由题意可知,,
对于二次函数,.
当时,,恒成立,f(x)在单调递减,有0个极值点;
当时,二次函数有2个大于零的零点,由数形结合可知,有2个极值点;
当时,二次函数只有1个大于零的零点,由数形结合可知,有1个极值点.
(2)要证,即证.
设,则,
在上为增函数,
∵,,
∴在上,存在唯一的m,使得,即,.
∴在上<0,h(x)单调递减;在上,>0,h(x)单调递增;
∴,当且仅当m=1时取等号,
∵,∴等号不成立,∴,
∴,从而原不等式得证.
5. (2023·湖南·临澧县第一中学二模)已知函数.
(1)当时,若在上存在最大值,求m的取值范围;
(2)讨论极值点的个数.
【答案】(1);
(2)当时,函数有一个极值点;当时,函数有两个极值点;
当时,函数没有极值点.
【解析】
(1)因为,所以,
因为函数的定义域为:,
所以当时,单调递减,
当时,单调递增,所以当时,函数有最大值,
因此要想在上存在最大值,只需,
所以m的取值范围为;
(2)
,
方程的判别式为.
(1)当时,即,此时方程没有实数根,
所以,函数单调递减,故函数没有极值点;
(2)当时,即,
此时,(当时取等号),所以函数单调递减,故函数没有极值点;
(3)当时,即,此时方程有两个不相等的实数根,
设两个实数根为,设,则,
函数的定义域为:,显然
当时,此时方程有两个不相等的正实数根,
此时当时,,函数单调递减,当时,,函数单调递增,当时,,函数单调递减,
因此当时,函数有极小值点,当时,函数有极大值点,
所以当时,函数有两个极值点,
当时,方程有一个正实数根和一个负根,或是一个正实数和零根,
当时,,函数单调递增,当时,,函数单调递减,所以当时,函数有极大值点,
因此当时,函数有一个极值点,
综上所述:当时,函数有一个极值点;
当时,函数有两个极值点;
当时,函数没有极值点.
6. (2023·江西·上饶市第一中学模拟预测)已知函数.
(1)当时,求函数的极值;
(2)若函数在无零点,求实数a的取值范围.
【答案】(1)极小值为,无极大值(2)
【解析】(1)由题知,当时,,
∴,令,.
∴时,,单调递减;
时,,单调递增.
∴是的极小值点,∴的极小值为,无极大值.
(2)由题知,
∴,;令,
∴,∵,∴恒成立,
∴单调递增,即单调递增.
①当时,∴,∴单调递增
∴恒成立,即在上无零点,∴.
②当时,令,,,又单调递增,
∴时,,时,,
∴在时单调递减,时,单调递增,
∴,又∵时,
∴,,即在上有零点,不合题意;
综上所述.
7. (2023·北京市十一学校高三阶段练习)已知函数
(1)当时,求曲线在点处的切线方程;
(2)判断函数的极值点的个数,并说明理由.
【答案】(1)
(2)综上:当或时,无极值点;当或或时,有两个极值点.
【解析】(1)当时,,定义域为,.
因为,所以.
所以在点处的切线方程为:,
即.
(2)函数定义域为,.
①当时,,显然无极值点;
②当时,,
所以在上单调递增,故此时无极值点.
③当时,令,解得或,
或时,,时,,
所以在和上单调递增,在上单调递减,
故此时有两个极值点.
④当时,令,解得或,
或时,,时,,
所以在和上单调递增,在上单调递减,
故此时有两个极值点.
⑤当时,令,解得或,
或时,,时,,
所以在和上单调递增,在上单调递减,
故此时有两个极值点.
综上:当或时,无极值点;
当或或时,有两个极值点.
8. (2023·四川省峨眉第二中学校)已知,函数.
(1)讨论的单调性;
(2)当时,若对恒成立,求实数b的最大值.
【答案】(1)答案见解析(2)
【解析】(1)的定义域为,,
当时,,在上单调递减.
当时,令;
令.
综上,当时,在上单调递减,
当时,在上单调递减,在上单调递增.
(2)∵,∴恒成立,
即恒成立,
令,则,
由,得;由,得,
故在上单调递减,在上单调递增,
∴,即,
故实数b的最大值是.
94 (2023·江苏·华罗庚中学三模)已知函数 ,(为自然对数的底数,).
(1)求函数的单调区间;
(2)若,,当时,,求的最小值.
【答案】(1)分类讨论,答案见解析.(2)1
【解析】(1)函数 的定义域为 , ,
①当时,对任意的 , ,
此时函数的减区间为,无增区间;
②当时,由 可得,由 可得,
此时函数的单调递增区间为,递减区间为;
综上所述,当时,函数的减区间为,无增区间;
当时,函数的单调递增区间为,递减区间为;
(2)
证明:当时,,
则 ,
令,其中,则 ,
所以函数在上单调递增,
因为,,所以存在唯一,
使得,即,可得,
当时, ,此时函数单调递增,
当时, ,此时函数单调递减,
所以,当时,
,
即,因为,,
综上所述,若,当时,,
即 ,所以的最小值为1;
综上,的最小值为1.
10. (2023·天津市新华中学)已知函数,其中且
(1)当时,求函数的极值;
(2)求函数的单调区间;
(3)若存在,使函数,在处取得最小值,试求的最大值.
【答案】(1)极大值为,极小值为(2)答案见解析(3)
【解析】
(1)当时,,则,
当时,;当时,;
在,上单调递增,在上单调递减,
的极大值为,极小值为.
(2)由题意得:,定义域为,
,
令,解得:,;
①当时,,则时,;当时,;
的单调递增区间为,单调递减区间为;
②当时,,
则当时,;当时,;
的单调递增区间为,单调递减区间为;
综上所述:当时,的单调递增区间为,单调递减区间为;当时,的单调递增区间为,单调递减区间为.
(3),,
当时,恒成立,
;
当时,不等式恒成立;
当时,不等式可化为:,
令,
,是开口方向向下的抛物线,
在闭区间上的最小值必在区间端点处取得,又,
只需,即,
有解,,解得:;
的最大值为.增
极大值
减
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.2.2 函数的性质(二)(精练)(提升版)(原卷版+解析版): 这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.2.2 函数的性质(二)(精练)(提升版)(原卷版+解析版),共26页。
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.2.1 函数的性质(一)(精练)(提升版)(原卷版+解析版): 这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 3.2.1 函数的性质(一)(精练)(提升版)(原卷版+解析版),共35页。试卷主要包含了单调性与奇偶性应用之解不等式等内容,欢迎下载使用。
2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.3 利用递推公式求通项(精练)(基础版)(原卷版+解析版): 这是一份2024年新高考专用数学第一轮复习讲义一隅三反基础版 4.3 利用递推公式求通项(精练)(基础版)(原卷版+解析版),共16页。












