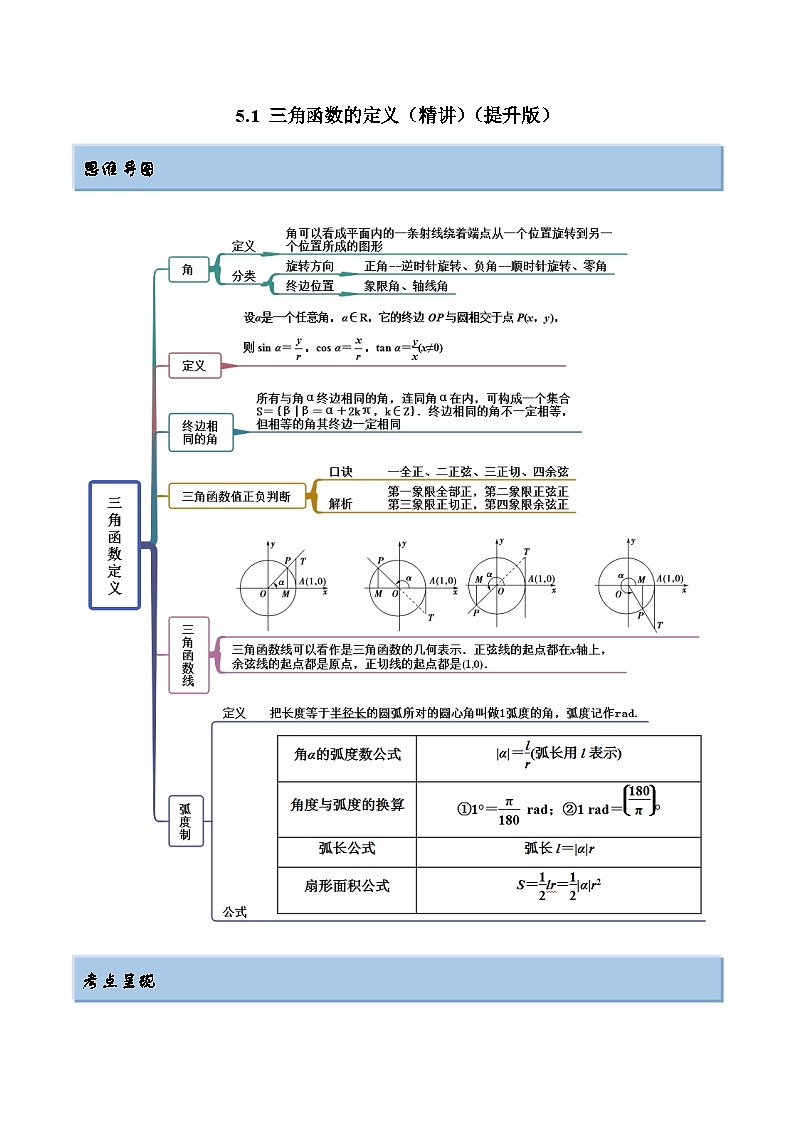
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.1 三角函数的定义（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.1 三角函数的定义（精讲）（提升版）（原卷版+解析版），共21页。试卷主要包含了三角函数的定义，判断三角函数值的正负，三角函数线等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 扇形的弧长与面积
【例1-1】 (2023·广东广东·一模）数学中处处存在着美，机械学家莱洛发现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形ABC，再分别以点A、B、C为圆心，线段AB长为半径画圆弧，便得到莱洛三角（如图所示）．若莱洛三角形的周长为，则其面积是______．

【例1-2】 (2023·江苏·徐州市第七中学高三阶段练习）已知点，是圆：上两点，动点从出发，沿着圆周按逆时针方向走到，其路径长度的最小值为（ ）
A．B．
C．D．
【例1-3】 (2023·贵州·贵阳一中高三阶段练习（文））在长方体中，，，，点P在长方体的面上运动，且满足，则P的轨迹长度为（ ）
A．12πB．8πC．6πD．4π
【一隅三反】
1． (2023·全国·高三专题练习）希波克拉底是古希腊医学家，他被西方尊为“医学之父”，除了医学，他也研究数学．特别是与“月牙形”有关的问题．如图所示．阴影郭分的月牙形的边缘都是圆弧，两段圆弧分别是的外接圆和以AB为直径的圆的一部分，若，，则该月牙形的面积为（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）在棱长为6的正方体中，点是线段的中点，是正方形（包括边界）上运动，且满足，则点的轨迹周长为________.
3． (2023·上海·高三专题练习）若球的半径为（为常量），且球面上两点，的最短距离为，经过，两点的平面截球所得的圆面与球心的距离为，则在此圆面上劣弧所在的弓形面积为___________.
考点二 三角函数的定义
【例2-1】 (2023·河南）在平面直角坐标系中，角的终边经过点，则的值是（ ）
A．B．或C．D．
【例2-2】 (2023·全国·模拟预测）已知角，的顶点为坐标原点，始边与x轴正半轴重合，角的终边过点，将角的终边顺时针旋转得到角的终边，则（ ）
A．B．C．D．
【一隅三反】
1． (2023·内蒙古赤峰·高三期末（文））在平面直角坐标系中，角和角的顶点均与原点O重合，始边均与x轴的非负半轴重合，它们的终边关于直线对称，若，则（ ）
A．B．C．D．
2． (2023·新疆昌吉·一模（文））在平面直角坐标系中，已知角的终边与圆相交于点，角满足，则的值为（ ）
A．B．C．D．
3． (2023·重庆八中高三阶段练习）在平面直角坐标系中，角的始边为轴的非负半轴，终边与单位圆的交点在第一象限内.若，则（ ）
A．B．C．D．
考点三 判断三角函数值的正负
【例3-1】． (2023·全国·高三专题练习）已知角第二象限角，且，则角是（ ）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
【例3-2】 (2023·陕西·西安中学模拟预测（文））已知，则（ ）
A．B．C．D．
【例3-3】 (2023·全国·高三专题练习（理））若，的化简结果是（ ）．
A．B．C．D．
【一隅三反】
1． (2023·重庆八中高三阶段练习）（多选）已知角的顶点与原点重合，始边与轴的非负半轴重合，终边经过点，若，则下列各式的符号无法确定的是（ ）
A．B．C．D．
2 (2023·全国·高三专题练习）已知是第二象限角，则下列选项中一定正确的是（ ）
A．B．C．D．
3． (2023·全国·高三专题练习（理））如图，在平面直角坐标系中，点为阴影区域内的动点（不包括边界），这里，则下列不等式恒成立的是（ ）
A．B．C．D．
考点四 三角函数线
【例4-1】 (2023·河南·高三阶段练习（文））已知，，，则（ ）
A．B．C．D．
【例4-2】 (2023·河南·南阳市第二完全学校高级中学高一阶段练习）已知，则的大小关系是（ ）
A．B．
C．D．
【一隅三反】
1． (2023·全国·高三专题练习）已知点在第一象限，则在内的的取值范围是（ ）
A．B．
C．D．
2． (2023·全国·高三专题练习）设,则下列命题:①;②;③是单调减函数.其中真命题的个数是
A．0B．1C．2D．3
3． (2023·全国·高三专题练习（文））在平面直角坐标系中，是圆上的四段弧（如图），点P在其中一段上，角以O?为始边，OP为终边，若，则P所在的圆弧是
A．B．
C．D．
5.1 三角函数的定义（精讲）（提升版）
思维导图
考点呈现
例题剖析
考点一 扇形的弧长与面积
【例1-1】 (2023·广东广东·一模）数学中处处存在着美，机械学家莱洛发现的莱洛三角形就给人以对称的美感．莱洛三角形的画法：先画等边三角形ABC，再分别以点A、B、C为圆心，线段AB长为半径画圆弧，便得到莱洛三角（如图所示）．若莱洛三角形的周长为，则其面积是______．
【答案】
【解析】由条件可知，弧长，等边三角形的边长，则以点A、B、C为圆心，圆弧所对的扇形面积为，中间等边的面积
所以莱洛三角形的面积是.故答案为：

【例1-2】 (2023·江苏·徐州市第七中学高三阶段练习）已知点，是圆：上两点，动点从出发，沿着圆周按逆时针方向走到，其路径长度的最小值为（ ）
A．B．
C．D．
【答案】C
【解析】设点在的终边，在的终边上，设,
，优弧的圆心角为
弧长=，故选:C
【例1-3】 (2023·贵州·贵阳一中高三阶段练习（文））在长方体中，，，，点P在长方体的面上运动，且满足，则P的轨迹长度为（ ）
A．12πB．8πC．6πD．4π
【答案】C
【解析】如图，在左侧面的轨迹为弧，在后侧面的轨迹为弧，在右侧面的轨迹为弧，在前侧面内的轨迹为弧.
易知，，又，，∴，则，
∴P的轨迹长度为6π，故选：C.
【一隅三反】
1． (2023·全国·高三专题练习）希波克拉底是古希腊医学家，他被西方尊为“医学之父”，除了医学，他也研究数学．特别是与“月牙形”有关的问题．如图所示．阴影郭分的月牙形的边缘都是圆弧，两段圆弧分别是的外接圆和以AB为直径的圆的一部分，若，，则该月牙形的面积为（ ）
A．B．C．D．
【答案】A
【解析】因为，，所以，所以，
设的外接圆的圆心为O，半径为R，如图所示，
由正弦定理得，所以，
内侧圆弧为的外接圆的一部分，且其对应的圆心角为，
则弓形的面积为，
外侧的圆弧以为直径，所以半圆的面积为，
则月牙形的面积为.故选：A．
2． (2023·全国·高三专题练习）在棱长为6的正方体中，点是线段的中点，是正方形（包括边界）上运动，且满足，则点的轨迹周长为________.
【答案】
【解析】如图，在棱长为6的正方体中，
则平面，平面，
又，在平面上，，，
又，，
，即，
如图，在平面中，以为原点，分别为轴建立平面直角坐标系，
则，，，
由，知，
化简整理得，，圆心，半径的圆，
所以点的轨迹为圆与四边形的交点，即为图中的
其中，，，则
由弧长公式知
故答案为：.
3． (2023·上海·高三专题练习）若球的半径为（为常量），且球面上两点，的最短距离为，经过，两点的平面截球所得的圆面与球心的距离为，则在此圆面上劣弧所在的弓形面积为___________.
【答案】
【解析】因为球的半径为，球面上两点，的最短距离为，所以，
设经过，两点的平面截球所得的圆面为圆，则平面，且，
所以截面圆圆的半径，
连接，因为，，所以线段，
在中，，，
由余弦定理可得：，所以，
所以在此圆面上劣弧所在的弓形面积为扇形的面积减去的面积，
即为： ，故答案为：.
考点二 三角函数的定义
【例2-1】 (2023·河南）在平面直角坐标系中，角的终边经过点，则的值是（ ）
A．B．或C．D．
【答案】D
【解析】．
因为，，，所以，所以，故选：D．
【例2-2】 (2023·全国·模拟预测）已知角，的顶点为坐标原点，始边与x轴正半轴重合，角的终边过点，将角的终边顺时针旋转得到角的终边，则（ ）
A．B．C．D．
【答案】C
【解析】由题知，点到原点的距离为，，，.故选：C.
【一隅三反】
1． (2023·内蒙古赤峰·高三期末（文））在平面直角坐标系中，角和角的顶点均与原点O重合，始边均与x轴的非负半轴重合，它们的终边关于直线对称，若，则（ ）
A．B．C．D．
【答案】C
【解析】角和角的终边关于直线对称，则，．
．故选：C．
2． (2023·新疆昌吉·一模（文））在平面直角坐标系中，已知角的终边与圆相交于点，角满足，则的值为（ ）
A．B．C．D．
【答案】B
【解析】由三角函数定义可知，，
，，，故选：．
3． (2023·重庆八中高三阶段练习）在平面直角坐标系中，角的始边为轴的非负半轴，终边与单位圆的交点在第一象限内.若，则（ ）
A．B．C．D．
【答案】C
【解析】因为角的终边与单位圆的交点在第一象限内，所以，.
因为，所以，即，
将代入，得，即，
解得，
当时，（舍）；
当时，；
所以.故选：C.
考点三 判断三角函数值的正负
【例3-1】． (2023·全国·高三专题练习）已知角第二象限角，且，则角是（ ）
A．第一象限角B．第二象限角C．第三象限角D．第四象限角
【答案】C
【解析】因为角第二象限角,所以，
所以，
当是偶数时，设，则，此时为第一象限角；
当是奇数时，设，则，此时为第三象限角.；
综上所述：为第一象限角或第三象限角，
因为，所以，所以为第三象限角．故选：C．
【例3-2】 (2023·陕西·西安中学模拟预测（文））已知，则（ ）
A．B．C．D．
【答案】C
【解析】因为，所以，，
所以
另解：因为，所以，，所以
．故选：C
【例3-3】 (2023·全国·高三专题练习（理））若，的化简结果是（ ）．
A．B．C．D．
【答案】C
【解析】由，，得，
故选：C．
【一隅三反】
1． (2023·重庆八中高三阶段练习）（多选）已知角的顶点与原点重合，始边与轴的非负半轴重合，终边经过点，若，则下列各式的符号无法确定的是（ ）
A．B．C．D．
【答案】AC
【解析】由三角函数定义，，
所以，对于A选项，当时，，时，，时，，所以选项A符号无法确定；
对于B选项， ，所以选项B符号确定；
对于C选项，，故当时，，时，，时，，所以选项C的符号无法确定；
对于D选项，，所以选项D符号确定.
所以下列各式的符号无法确定的是AC选项.
故选：AC.
2 (2023·全国·高三专题练习）已知是第二象限角，则下列选项中一定正确的是（ ）
A．B．C．D．
【答案】C
【解析】因为是第二象限角，所以，，则，，
所以为第三或第四象限角或终边在轴负半轴上，所以选项A不一定正确；
可能不存在，选项B也不一定正确；又，，是第一象限或第三象限角，
则选项C正确，选项D不一定正确.故选:C．
3． (2023·全国·高三专题练习（理））如图，在平面直角坐标系中，点为阴影区域内的动点（不包括边界），这里，则下列不等式恒成立的是（ ）
A．B．C．D．
【答案】A
【解析】由于，则．设与相平行的直线的方程为，
当直线过点时，；
当直线过点和时，；
直线过点和时，．
则由图中阴影部分可得或，
这里．则一定有．
考点四 三角函数线
【例4-1】 (2023·河南·高三阶段练习（文））已知，，，则（ ）
A．B．C．D．
【答案】D
【解析】因为时，，，所以，
又，所以故选：D
【例4-2】 (2023·河南·南阳市第二完全学校高级中学高一阶段练习）已知，则的大小关系是（ ）
A．B．
C．D．
【答案】C
【解析】先证明：当0＜x＜时，
如图，角x终边为OP，其中点P为角x的终边与单位圆的交点，PM⊥x轴，交x轴与点M，
A点为单位圆与x轴的正半轴的交点，AT⊥x轴，交角x终边于点T，
则有向线段MP为角x的正弦线，有向线段AT为角x的正切线，设弧PA＝l＝x×1＝x，
由图形可知：S△OAP＜S扇形OAP＜S△OAT，
即
所以＜＜，即
所以
又由函数在上单调递增，所以
又由函数在上单调递减，则
所以
所以，即
故选：C．
【一隅三反】
1． (2023·全国·高三专题练习）已知点在第一象限，则在内的的取值范围是（ ）
A．B．
C．D．
【答案】B
【解析】由已知点在第一象限得：
，，即，，
当，可得，．
当，可得或，．
或，．
当时，或．
，
或．
故选：B．
2． (2023·全国·高三专题练习）设,则下列命题:①;②;③是单调减函数.其中真命题的个数是
A．0B．1C．2D．3
【答案】D
【解析】对于①，在如图所示的单位圆中，
设，则,因为，
所以由可得，即，所以①正确；
对于②，令，
所以，
因为，所以，
所以在上递增，所以，即，即，
所以②正确；
对于③，因为，所以，由②知，
所以，所以为上的递减函数，故③正确.
故选：D
3． (2023·全国·高三专题练习（文））在平面直角坐标系中，是圆上的四段弧（如图），点P在其中一段上，角以O?为始边，OP为终边，若，则P所在的圆弧是
A．B．
C．D．
【答案】C
【解析】由下图可得：有向线段为余弦线，有向线段为正弦线，有向线段为正切线.
A选项：当点在上时，，
，故A选项错误；
B选项：当点在上时，，，
，故B选项错误；
C选项：当点在上时，，，
，故C选项正确；
D选项：点在上且在第三象限，，故D选项错误.
综上，故选C.