2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.4 求和方法（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 6.4 求和方法（精讲）（提升版）（原卷版+解析版），共41页。试卷主要包含了公式法求和，裂项相消求和，错位相减求和，分组转化求和，周期数列，倒序相加法等内容，欢迎下载使用。

考点呈现
例题剖析
考点一 公式法求和
【例1】 (2023·江苏江苏·高三期末）已知数列满足.
(1)设，求数列的通项公式；
(2)设，求数列的前20项和.
【一隅三反】
1． (2023·全国·模拟预测）设数列的前n项和为，且.
(1)求；
(2)证明：当时，.
2． (2023·湖南·一模）已知数列的前n项和为，．
(1)证明：数列为等比数列；
(2)记数列的前n项和为，证明：．
3． (2023·广东深圳·一模）已知数列的首项，且满足．
(1)证明：是等比数列；
(2)求数列的前n项和．
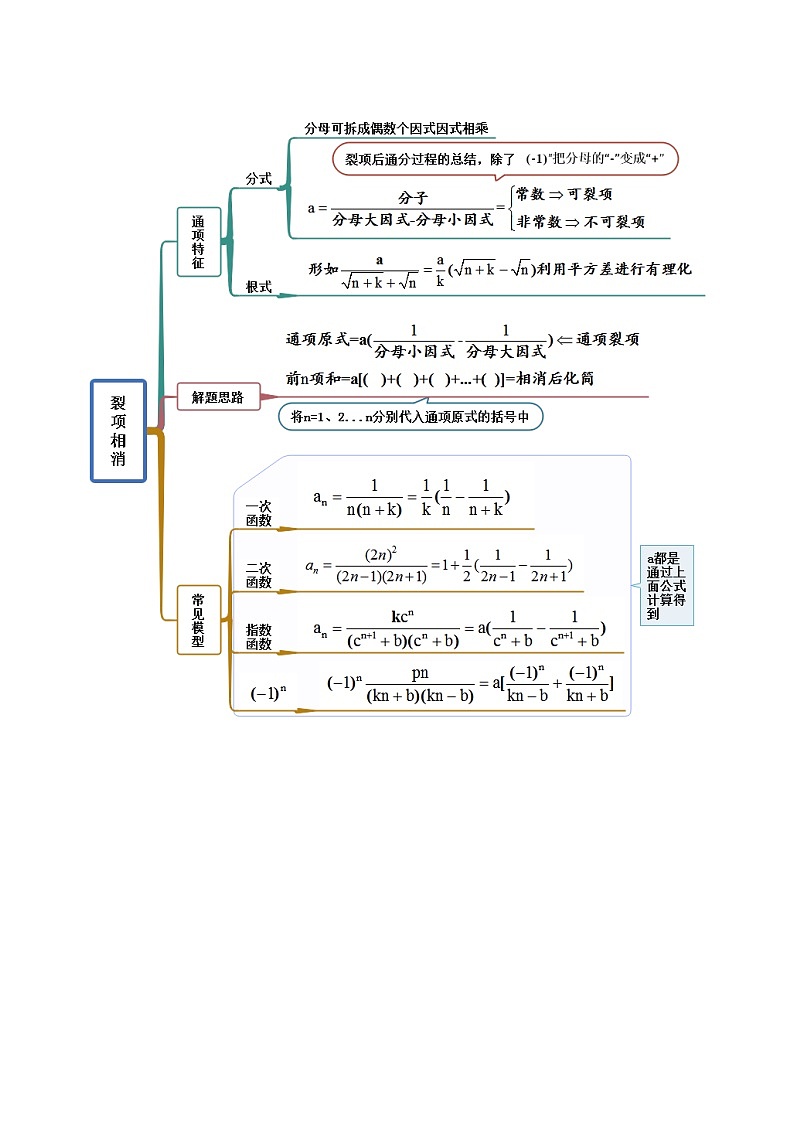
考点二 裂项相消求和
【例2-1】 (2023·辽宁·鞍山一中模拟预测）已知是等差数列的前项和，，，公差，且___________.从①为与等比中项，②等比数列的公比为，这两个条件中，选择一个补充在上面问题的横线上，使得符合条件的数列存在并作答.
(1)求数列的通项公式；
(2)设数列的前项和为，求证：.
【例2-2】 (2023·广东肇庆·模拟预测）已知数列是等比数列，且，.
(1)求数列的通项公式；
(2)设，求数列的前n项和，并证明：.
【例2-3】 (2023·广东梅州·二模）已知是数列的前项和，，___________.
①，；②数列为等差数列，且的前项和为.从以上两个条件中任选一个补充在横线处，并求解：
(1)求；
(2)设，求数列的前项和.
【例2-4】 (2023·广东茂名·二模）已知数列满足，，．
(1)证明：数列是等比数列；
(2)若，求数列的前项和．
【一隅三反】
1． (2023·广东梅州·二模）已知是数列的前项和，，___________.
①，；②数列为等差数列，且的前项和为.从以上两个条件中任选一个补充在横线处，并求解：
(1)求；
(2)设，求数列的前项和.
2． (2023·全国·模拟预测）已知数列满足，.
(1)求的通项公式；
(2)若，求的前n项和.
3． (2023·全国·模拟预测）已知正项数列的前n项和为，给出以下三个条件：①，；②；③，.从这三个条件中任选一个解答下面的问题.
(1)求数列的通项公式；
(2)设，求数列的前n项和.
注：如果选择多个条件分别解答，按第一个解答计分
4． (2023·江苏南通·模拟预测）已知正项数列{}中，，是其前n项和，且满足
(1)求数列{}的通项公式：
(2)已知数列{}满足，设数列{}的前n项和为，求的最小值.
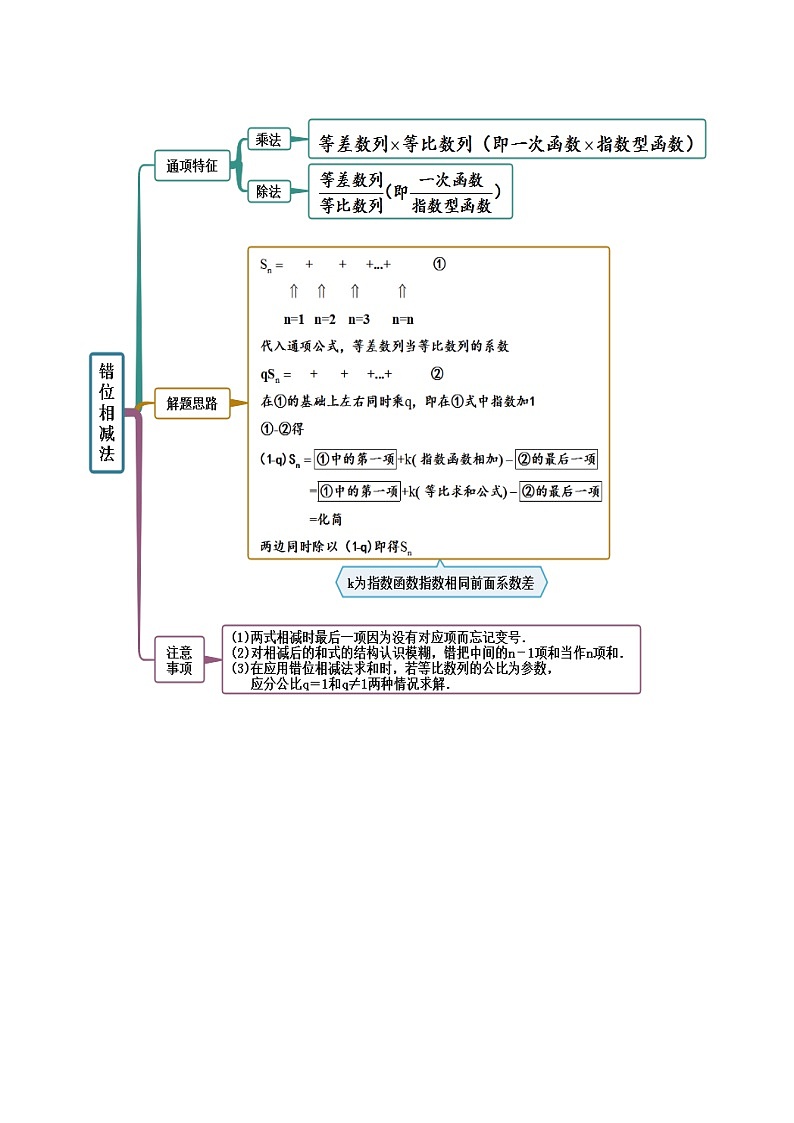
考点三 错位相减求和
【例3】 (2023·广东茂名·二模）已知数列的前n项和为，且．
(1)求证：数列为等差数列；
(2)求数列的前n项和．
【一隅三反】
1． (2023·广东广东·一模）设数列的前n项和为，满足，且．
(1)求数列的通项公式；
(2)设，求的前n项和．
2． (2023·浙江·高考真题）已知数列的前n项和为，，且.
（1）求数列的通项；
（2）设数列满足，记的前n项和为，若对任意恒成立，求实数的取值范围.
3． (2023·全国·高考真题（理））记为数列的前n项和，为数列的前n项积，已知．
（1）证明：数列是等差数列;
（2）求的通项公式．
考点四 分组转化求和
【例4-1】 (2023·全国·模拟预测（理））已知正项数列的前n项和为，满足.
(1)求数列的通项公式；
(2)求数列的前n项和.
【例4-2】 (2023·山东日照·模拟预测）已知数列中，，，（），，，，成等差数列．
(1)求k的值和的通项公式；
(2)设，求数列的前n项和．
【一隅三反】
1． (2023·安徽·高三期末（理））已知数列的前n项和．
(1)求数列的通项公式；
(2)设，求数列的前项和．
2． (2023·全国·模拟预测（理））已知数列满足，且．
(1)求数列的通项公式；
(2)若，求数列的前2n项的和
3． (2023·湖南·高三阶段练习）已知数列中，，，令.
(1)求数列的通项公式；
(2)若，求数列的前14项和.
考点五 周期数列
【例5】 (2023·江西赣州·一模）设正项数列的前项和为，已知.
(1)求的通项公式；
(2)记，是数列的前项和，求.
【一隅三反】
1． (2023·江苏·高三专题练习）已知数列的通项公式，，其前项和为，则______．
2． (2023·全国·高三专题练习（理））数列的通项公式为，前项和为，则＝________.
考点六 倒序相加法
【例6】 (2023·全国·高三专题练习）已知函数，数列满足，则（ ）
A．2018B．2019C．4036D．4038
【一隅三反】
1． (2023·全国·高三专题练习）已知函数，则的值为（ ）
A．1B．2C．2020D．2021
2． (2023·全国·高三专题练习）已知是上的奇函数，，则数列的通项公式为（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）已知函数，则（ ）
A．2018B．2019
C．4036D．4038
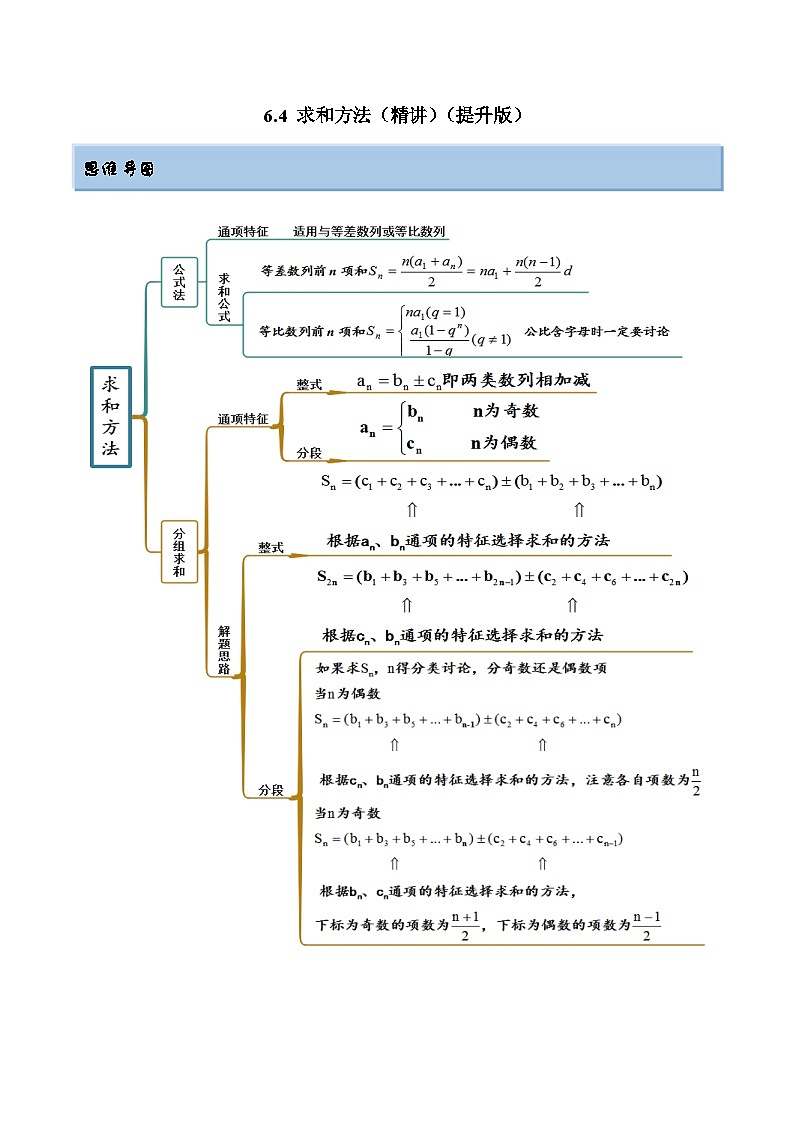
6.4 求和方法（精讲）（提升版）
思维导图
考点呈现
例题剖析
考点一 公式法求和
【例1】 (2023·江苏江苏·高三期末）已知数列满足.
(1)设，求数列的通项公式；
(2)设，求数列的前20项和.
【答案】(1)(2)
【解析】(1)由可知，，即，
由可知，，
所以是以12为首项，4为公比的等比数列，
所以的通项公式为.
(2)由（1）知，，
所以,
又符合上式,所以,所以，
所以的前20项和.
【一隅三反】
1． (2023·全国·模拟预测）设数列的前n项和为，且.
(1)求；
(2)证明：当时，.
【答案】(1)(2)见解析
【解析】(1)当时，，解得，
当时，，
即，
是以为首项，为公比的等比数列，
则，即，
(2)由，得，
则，令，则，
令，则，当时，，
在上单调递增，，即，
当且仅当时，取等，得证.
2． (2023·湖南·一模）已知数列的前n项和为，．
(1)证明：数列为等比数列；
(2)记数列的前n项和为，证明：．
【答案】(1)证明见解析；(2)证明见解析.
【解析】
(1)，，∴，
故数列为等比数列，首项为，公比为2；
(2)由(1)可知，∴，.
3． (2023·广东深圳·一模）已知数列的首项，且满足．
(1)证明：是等比数列；
(2)求数列的前n项和．
【答案】(1)证明见解析(2)
【解析】(1)由，得， 又，故，
故，所以， 所以数列是以为首项，为公比的等比数列．
(2)由（1）可知，所以，
所以．
考点二 裂项相消求和
【例2-1】 (2023·辽宁·鞍山一中模拟预测）已知是等差数列的前项和，，，公差，且___________.从①为与等比中项，②等比数列的公比为，这两个条件中，选择一个补充在上面问题的横线上，使得符合条件的数列存在并作答.
(1)求数列的通项公式；
(2)设数列的前项和为，求证：.
【答案】(1)选择条件见解析，(2)证明见解析
【解析】(1)若选①，为与的等比中项，
则，由为等差数列，，得，∴，
把代入上式，可得，解得或（舍）
∴，；
若选②，为等比数列的公比，且，
可得，即，即有，即；
又，可得，即，解得，此时；
(2)∵，
∴；∴，得证
【例2-2】 (2023·广东肇庆·模拟预测）已知数列是等比数列，且，.
(1)求数列的通项公式；
(2)设，求数列的前n项和，并证明：.
【答案】(1)(2)，证明见解析.
【解析】(1)设等比数列的公比是q，首项是.
由，可得.
由，可得，所以，
所以；
(2)证明：因为，
所以
.
又，所以.
【例2-3】 (2023·广东梅州·二模）已知是数列的前项和，，___________.
①，；②数列为等差数列，且的前项和为.从以上两个条件中任选一个补充在横线处，并求解：
(1)求；
(2)设，求数列的前项和.
【答案】(1)条件选择见解析，(2)
【解析】(1)解：选条件①：，，得，
所以，，
即数列、均为公差为的等差数列，
于是，
又，，，所以；
选条件②：因为数列为等差数列，且的前项和为，
得，所以，
所以的公差为，
得到，则，
当，.
又满足，所以，对任意的，.
(2)解：因为，
所以
.
【例2-4】 (2023·广东茂名·二模）已知数列满足，，．
(1)证明：数列是等比数列；
(2)若，求数列的前项和．
【答案】(1)证明见解析(2)
【解析】(1)由得：，又，
数列是以为首项，为公比的等比数列.
(2)由（1）得：，
则，，，…，，
各式作和得：，
又，，
，
当为偶数时，；
当为奇数时，；
综上所述：.
【一隅三反】
1． (2023·广东梅州·二模）已知是数列的前项和，，___________.
①，；②数列为等差数列，且的前项和为.从以上两个条件中任选一个补充在横线处，并求解：
(1)求；
(2)设，求数列的前项和.
【答案】(1)条件选择见解析，(2)
【解析】(1)解：选条件①：，，得，
所以，，
即数列、均为公差为的等差数列，
于是，
又，，，所以；
选条件②：因为数列为等差数列，且的前项和为，
得，所以，
所以的公差为，
得到，则，
当，.
又满足，所以，对任意的，.
(2)解：因为，
所以
.
2． (2023·全国·模拟预测）已知数列满足，.
(1)求的通项公式；
(2)若，求的前n项和.
【答案】(1)(2)
【解析】(1)解：由，可得，即，
所以当时，，，，，
将上述式子进行累加得，-
将代入可得，即.
当时也满足上式，
所以数列的通项公式.
(2)解：由（1）得，
则.
3． (2023·全国·模拟预测）已知正项数列的前n项和为，给出以下三个条件：①，；②；③，.从这三个条件中任选一个解答下面的问题.
(1)求数列的通项公式；
(2)设，求数列的前n项和.
注：如果选择多个条件分别解答，按第一个解答计分
【答案】(1)(2)
【解析】(1)若选①：由，得.
令，，可得.
当时，，，…，，
累加得.
又，则，则.
又也适合上式，所以.
若选②：由，可得.
又是正项数列，所以，所以，则.
当时，.
又也适合上式，所以.
若选③：由得，当时，，两式作差得
，整理得.
由于，故，即是首项为1，公差为2的等差数列，所以.
(2)由（1）得，，
则，
所以
.
4． (2023·江苏南通·模拟预测）已知正项数列{}中，，是其前n项和，且满足
(1)求数列{}的通项公式：
(2)已知数列{}满足，设数列{}的前n项和为，求的最小值.
【答案】(1)(2)
【解析】(1)正项数列{}，，满足，所以，
所以数列{}是以1为首项1为公差的等差数列，
所以，所以，
当时，，
当时也成立，
所以.
(2)因为
所以，
所以当为奇数时，；
当为偶数时，，
由{}递增，得，
所以的最小值为.
考点三 错位相减求和
【例3】 (2023·广东茂名·二模）已知数列的前n项和为，且．
(1)求证：数列为等差数列；
(2)求数列的前n项和．
【答案】(1)证明见解析(2)
【解析】(1)由可得，
由得，
所以，即，
所以，，
所以数列是公差为1，首项为1的等差数列.
(2)由（1），得，
所以，
，两式相减得
，
所以.
【一隅三反】
1． (2023·广东广东·一模）设数列的前n项和为，满足，且．
(1)求数列的通项公式；
(2)设，求的前n项和．
【答案】(1)(2)
【解析】(1)当时，，
得
即，即
所以数列是首项为2，公比为2的等比数列，故．
(2)由（1）知，则
（1）
（2）
（1）－（2）得
所以
2． (2023·浙江·高考真题）已知数列的前n项和为，，且.
（1）求数列的通项；
（2）设数列满足，记的前n项和为，若对任意恒成立，求实数的取值范围.
【答案】（1）；（2）.
【解析】（1）当时，，
，
当时，由①，
得②，①②得
，
又是首项为，公比为的等比数列，
；
（2）由，得，
所以，
，
两式相减得
，
所以，
由得恒成立，
即恒成立，
时不等式恒成立；
时，，得；
时，，得；
所以.
3． (2023·全国·高考真题（理））记为数列的前n项和，为数列的前n项积，已知．
（1）证明：数列是等差数列;
（2）求的通项公式．
【答案】（1）证明见解析；（2）.
【解析】（1）[方法一]：
由已知得,且，,
取,由得,
由于为数列的前n项积，
所以,
所以，
所以,
由于
所以，即,其中
所以数列是以为首项，以为公差等差数列;
[方法二]【最优解】：
由已知条件知 ①
于是． ②
由①②得． ③
又， ④
由③④得．
令，由，得．
所以数列是以为首项，为公差的等差数列．
[方法三]：
由，得，且，，．
又因为，所以，所以．
在中，当时，．
故数列是以为首项，为公差的等差数列．
[方法四]：数学归纳法
由已知，得，，，，猜想数列是以为首项，为公差的等差数列，且．
下面用数学归纳法证明．
当时显然成立．
假设当时成立，即．
那么当时，．
综上，猜想对任意的都成立．
即数列是以为首项，为公差的等差数列．
（2）
由（1）可得，数列是以为首项，以为公差的等差数列，
,
,
当n=1时，,
当n≥2时,,显然对于n=1不成立,
∴.
考点四 分组转化求和
【例4-1】 (2023·全国·模拟预测（理））已知正项数列的前n项和为，满足.
(1)求数列的通项公式；
(2)求数列的前n项和.
【答案】(1)(2)
【解析】(1)时，，又，解得，
由得，
时，，
两式相减得，
，又，所以，是等差数列，
所以；
(2)由（1），，
，
为偶数时，，
为奇数时，，
所以．
【例4-2】 (2023·山东日照·模拟预测）已知数列中，，，（），，，，成等差数列．
(1)求k的值和的通项公式；
(2)设，求数列的前n项和．
【答案】(1)，(2)
【解析】(1)解：，，成等差数列，
所以，
得，得，
因为，所以，
所以，得．
(2)由（1）知，
当n为偶数时，设n＝2k，
可得
，
即；
当n为奇数时，设n＝2k－1，
可得
，
即．
综上所述，.
【一隅三反】
1． (2023·安徽·高三期末（理））已知数列的前n项和．
(1)求数列的通项公式；
(2)设，求数列的前项和．
【答案】(1)(2)
【解析】(1)解：当时，，
当时，，
当时，上式也成立，
所以；
(2)解：，
设数列的前项和为，
则
.
2． (2023·全国·模拟预测（理））已知数列满足，且．
(1)求数列的通项公式；
(2)若，求数列的前2n项的和
【答案】(1)(2)
【解析】(1)∵，，，∴，
∴，
∴，，，…，，
将上述式子左右分别相乘得，
∴．
∵满足上式，
∴．
(2)∵，令，，
的前项和为，的前项和为，
∴，
，
∴．
3． (2023·湖南·高三阶段练习）已知数列中，，，令.
(1)求数列的通项公式；
(2)若，求数列的前14项和.
【答案】(1)(2)
【解析】(1)当时，，又，得，
由①
得②，①②两式相除可得，
则，且，
所以数列是以2为首项，2为公比的等比数列，
故.
(2)当n为奇数时，；
当n为偶数时，，
.
所以数列的前14项和为
.
考点五 周期数列
【例5】 (2023·江西赣州·一模）设正项数列的前项和为，已知.
(1)求的通项公式；
(2)记，是数列的前项和，求.
【答案】(1)(2)
【解析】(1)解：当时，，所以，又，故；
当时，，而，两式相减得，
整理得，因为，所以，
故是以为公差的等差数列，从而.
(2)解：，
设
，其中，
所以.
【一隅三反】
1． (2023·江苏·高三专题练习）已知数列的通项公式，，其前项和为，则______．
【答案】1010
【解析】，周期
故答案为：
2． (2023·全国·高三专题练习（理））数列的通项公式为，前项和为，则＝________.
【答案】
【解析】 ，，，，又的周期为，

故答案为：
考点六 倒序相加法
【例6】 (2023·全国·高三专题练习）已知函数，数列满足，则（ ）
A．2018B．2019C．4036D．4038
【答案】A
【解析】∵，∴．
又∵，∴．
令，则，
两式相加得，∴．故选：A
【一隅三反】
1． (2023·全国·高三专题练习）已知函数，则的值为（ ）
A．1B．2C．2020D．2021
【答案】C
【解析】函数，设，则有，
所以，
所以当时，，
令，
所以，
故．故选：C
2． (2023·全国·高三专题练习）已知是上的奇函数，，则数列的通项公式为（ ）
A．B．C．D．
【答案】C
【解析】由题已知是上的奇函数，故，
代入得：， ∴函数关于点对称，
令，则，得到，
∵，，
倒序相加可得，即，故选：C．
3． (2023·全国·高三专题练习）已知函数，则（ ）
A．2018B．2019
C．4036D．4038
【答案】A
【解析】，，令，
则，两式相加得：，.故选：.