
所属成套资源:2024年新高考数学专用第一轮复习讲义一隅三反提升卷【精讲+精练】(提升版)(原卷版+解析版)
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.2 空间几何的体积与表面积(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.2 空间几何的体积与表面积(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.4 空间距离(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.4 空间距离(精练)(提升版)(原卷版+解析版) 试卷 0 次下载
- 2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.5 外接球(精讲)(提升版)(原卷版+解析版) 试卷 0 次下载
2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.3 空间角(精讲)(提升版)(原卷版+解析版)
展开
这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.3 空间角(精讲)(提升版)(原卷版+解析版),共29页。试卷主要包含了线线角,线面角,二面角,空间角的综合运用等内容,欢迎下载使用。
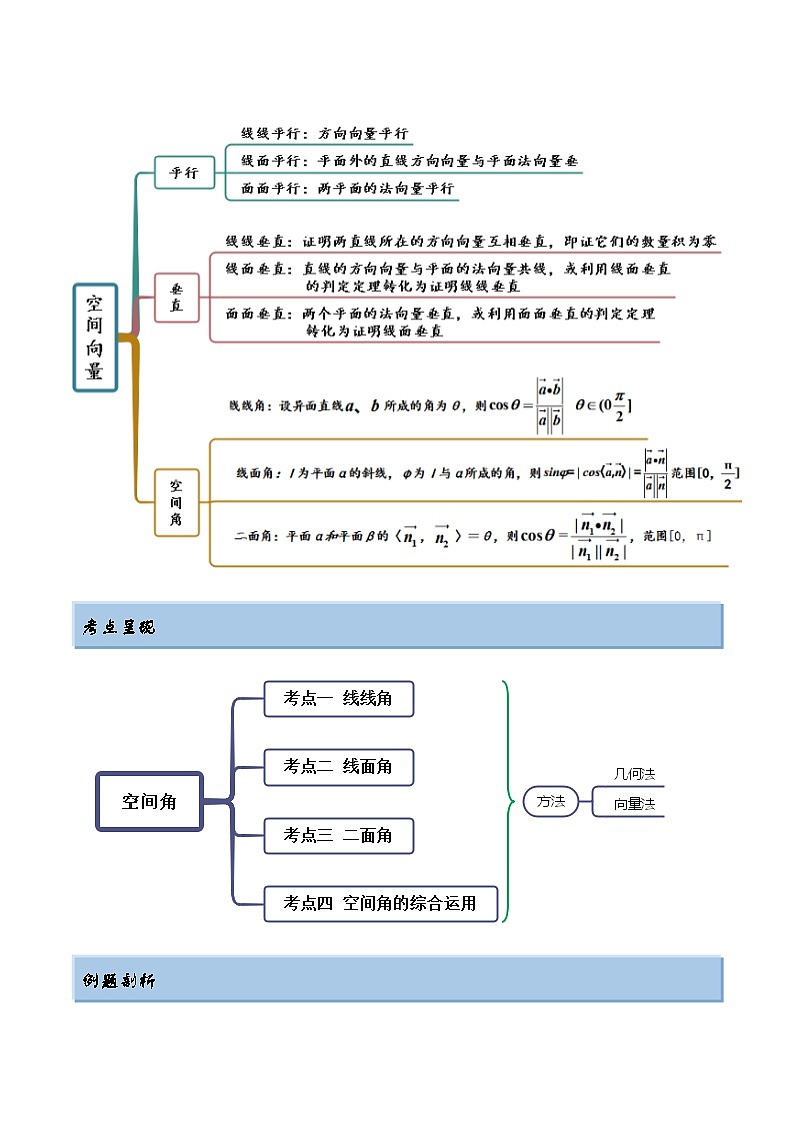
考点呈现
例题剖析
考点一 线线角
【例1-1】 (2023·全国·高三专题练习)如图,在三棱锥中,平面,是边长为的正三角形,,是的中点,则异面直线与所成角的余弦值是( )
A.B.
C.D.
【一隅三反】
1. (2023·新疆·三模(理))在正方体中,E为的中点,平面与平面的交线为l,则l与所成角的余弦值为( )
A.B.C.D.
2. (2023·四川内江·模拟预测(理))如图,在直三棱柱中,面,,则直线与直线夹角的余弦值为( )
A.B.C.D.
3. (2023·全国·高三专题练习)在三棱锥P—ABC中,PA、PB、PC两两垂直,且PA=PB=PC,M、N分别为AC、AB的中点,则异面直线PN和BM所成角的余弦值为( )
A.B.C.D.
考点二 线面角
【例2-1】 (2023·黑龙江)如图,在四棱锥中,底面是矩形,平面,,,且.
(1)求证:平面平面;
(2)若,,求直线PB与平面ADP所成角的正弦值.
【例2-2】 (2023·云南)已知正方体的棱长为1,点P在线段上,且,则AP与平面ABCD所成角的正切值为( )
A.1B.C.D.
【例2-3】. (2023·河南安阳)如图,在圆锥中,为圆锥的底面直径,为等腰直角三角形,B为底面圆周上一点,且,M为上一动点,设直线与平面所成的角为,则的最大值为( )
A.B.C.D.
【一隅三反】
1. (2023·河南安阳)如图,在四面体ABCD中,,,E为BD的中点,F为AC上一点.
(1)求证:平面平面BDF;
(2)若,,,求直线BF与平面ACD所成角的正弦值的最大值.
2. (2023·北京)如图,四棱锥的底面是梯形,,,E为线段中点.
(1)证明:;
(2)求直线与平面所成角的正弦值.
考点三 二面角
【例3-1】 (2023·云南师大附中)如图,是边长为的等边三角形,E,F分别是的中点,G是的重心,将沿折起,使点A到达点P的位置,点P在平面的射影为点G.
(1)证明:;
(2)求平面与平面夹角的余弦值.
【例3-2】 (2023·青海·海东市第一中学)如图,在四棱锥P-ABCD中,平面平面ABCD,为等边三角形,,,M是棱上一点,且.
(1)求证:平面MBD;
(2)求二面角M-BD-C的余弦值.
【一隅三反】
1. (2023·天津·高考真题)直三棱柱中,,D为的中点,E为的中点,F为的中点.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面所成二面角的余弦值.
2. (2023·江西)如图,在三棱锥中,是边长为2的正三角形,,,D为上靠近A的三等分点.
(1)若,求证:平面平面;
(2)当三棱锥的体积最大时,求二面角的余弦值.
3. (2023·广西玉林·模拟预测(理))如图,在直三棱柱 中,D,E别是棱、上的点,,.
(1)求证:平面平面;
(2)若直线与平面ABC所成的角为,且,求二面角的大小.
考点四 空间角的综合运用
【例4】 (2023·重庆南开中学)(多选)已知正四棱锥的侧面是边长为6的正三角形,点M在棱PD上,且,点Q在底面及其边界上运动,且面,则下列说法正确的是( )
A.点Q的轨迹为线段
B.与CD所成角的范围为
C.的最小值为
D.二面角的正切值为
【一隅三反】
1. (2023·湖南·长郡中学模拟预测)(多选)已知正方体的边长为2,M为的中点,P为侧面上的动点,且满足平面,则下列结论正确的是( )
A.B.平面
C.与所成角的余弦值为D.动点P的轨迹长为
2. (2023·福建·三明一中模拟预测)已知正方体中,,点E为平面内的动点,设直线与平面所成的角为,若,则点E的轨迹所围成的面积为___________.
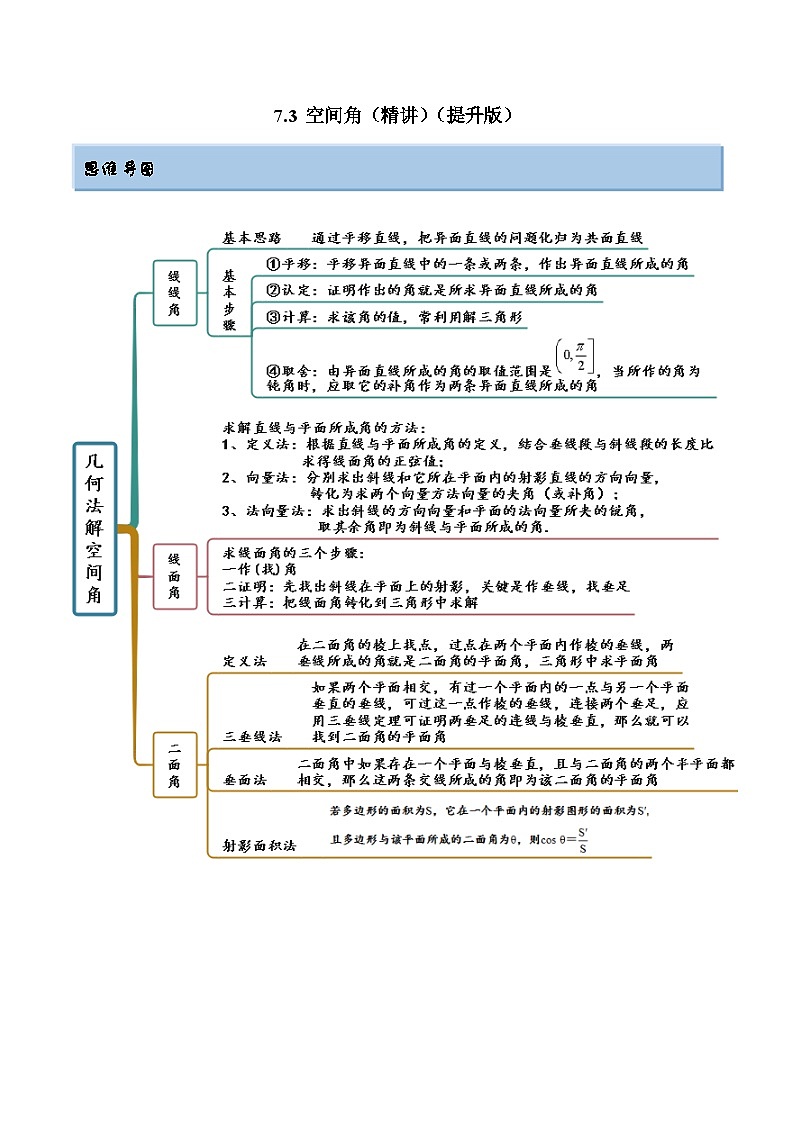
7.3 空间角(精讲)(提升版)
思维导图
考点呈现
例题剖析
考点一 线线角
【例1-1】 (2023·全国·高三专题练习)如图,在三棱锥中,平面,是边长为的正三角形,,是的中点,则异面直线与所成角的余弦值是( )
A.B.
C.D.
【答案】D
【解析】解法一:设E为BC的中点,连接FE,如图,
∵E是BC的中点,
∴∥,,,;
在中,由余弦定理可知
∴异面直线BE与AF所成角的余弦值为,
解法二:以A为坐标原点,AC,AM所在直线分别为y,z轴建立空间直角坐标系如图所示,
易知,,,
所以,,
则,
∴异面直线BE与AF所成角的余弦值为.故选:D
【一隅三反】
1. (2023·新疆·三模(理))在正方体中,E为的中点,平面与平面的交线为l,则l与所成角的余弦值为( )
A.B.C.D.
【答案】D
【解析】延长,交直线于点M,延长交于点,连接,
则直线即为交线,
又,则即为l与所成的角,设正方体棱长为1,
因为E为的中点,,
所以为的中点,为的中点,点为的中点,为的中点,则,
又,所以,所以,
则,,,所以,
即l与所成角的余弦值为.故选:D.
2. (2023·四川内江·模拟预测(理))如图,在直三棱柱中,面,,则直线与直线夹角的余弦值为( )
A.B.C.D.
【答案】C
【解析】连接交于,若是的中点,连接,
由为直棱柱,各侧面四边形为矩形,易知:是的中点,
所以,故直线与直线夹角,即为与的夹角或补角,
若,则,,
面,面,则,
而,又,面,故面,
又面,所以.
所以,,
在△中.
故选:C
3. (2023·全国·高三专题练习)在三棱锥P—ABC中,PA、PB、PC两两垂直,且PA=PB=PC,M、N分别为AC、AB的中点,则异面直线PN和BM所成角的余弦值为( )
A.B.C.D.
【答案】B
【解析】以点P为坐标原点,以,,方向为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,
令,则,,,,
则,,
设异面直线PN和BM所成角为,则.故选:B.
考点二 线面角
【例2-1】 (2023·黑龙江)如图,在四棱锥中,底面是矩形,平面,,,且.
(1)求证:平面平面;
(2)若,,求直线PB与平面ADP所成角的正弦值.
【答案】(1)证明见解析(2)
【解析】(1)因为,所以,所以,
又因为,所以,所以,所以,
又因为平面,平面,所以,
又因为,平面,所以平面,
而平面,所以平面平面.
得证.
(2)如图,以为坐标原点,分别以、、所在的直线为坐标轴正方向建立空间直角坐标系,则点,,,,则
,,,
设平面的法向量为,则,即,
令可得平面的法向量为,
设直线PB与平面ADP所成角为,则
.
直线PB与平面ADP所成角的正弦值为.
【例2-2】 (2023·云南)已知正方体的棱长为1,点P在线段上,且,则AP与平面ABCD所成角的正切值为( )
A.1B.C.D.
【答案】D
【解析】如图,连接,
因为在平面ABCD上的投影为,故作于,且平面,
连接,则AP与平面ABCD所成角为.
因为,故,且,故.
所以AP与平面ABCD所成角的正切值为
故选:D
【例2-3】. (2023·河南安阳)如图,在圆锥中,为圆锥的底面直径,为等腰直角三角形,B为底面圆周上一点,且,M为上一动点,设直线与平面所成的角为,则的最大值为( )
A.B.C.D.
【答案】C
【解析】如图,过点作于点,连,∵平面,平面,∴,又,,平面,∴平面,又∵平面,∴,故为直线与平面所成的角,在中,越小,越大,越大,当时,最小,此时最大,∵为等腰直角三角形,又,在中,,在中,,则,在等腰直角三角形中,,在中,,,则,
故选:C.
【一隅三反】
1. (2023·河南安阳)如图,在四面体ABCD中,,,E为BD的中点,F为AC上一点.
(1)求证:平面平面BDF;
(2)若,,,求直线BF与平面ACD所成角的正弦值的最大值.
【答案】(1)证明见解析;(2).
【解析】(1)在四面体ABCD中,,E为BD的中点,则,
而,平面,于是得平面,又平面,所以平面平面.
(2)依题意不妨设,,则,又,则,.
在中,,所,则,.
由(1)得,,因,即,则.
设点B到平面ACD的距离为h,则,解得,所以点B到平面ACD的距离为.
设直线BF与平面ACD所成角为,所以.
因为,所以,故当时,最短,此时,正弦值最大为.
2. (2023·北京)如图,四棱锥的底面是梯形,,,E为线段中点.
(1)证明:;
(2)求直线与平面所成角的正弦值.
【答案】(1)证明见解析;(2).
【解析】(1)取中点F,连接交于点O,连接,
由,且梯形,有且,
故平行四边形,又,故为菱形,
所以为的中点,故.
又因为,故,
因为,面,
故面,又面,故.
(2)解析1:几何法
在中,,故,
因为,故,由,即,
即,故面,
又,故面,面,故面面,
作,面面,面,故面,
在中,,因为,故B到面距离等于,
设与平面所成角为,,
故,故与平面所成角的正弦值为.
解析2:向量法
在中,,故,
因为,故,由,即,
即,故面,
以为x轴,为y轴,为z轴建立空间直角坐标系,
故,
故,
设面的法向量为,则,令,故,
所以,故与平面所成角的正弦值为.
考点三 二面角
【例3-1】 (2023·云南师大附中)如图,是边长为的等边三角形,E,F分别是的中点,G是的重心,将沿折起,使点A到达点P的位置,点P在平面的射影为点G.
(1)证明:;
(2)求平面与平面夹角的余弦值.
【答案】(1)证明见解析;(2)
【解析】(1)
连接,因是等边三角形,是的中点,是的重心,所以在上,,
又点在平面的射影为点,即平面,平面,所以,
又,所以平面,又平面,所以.
(2)
过点作,连接,与,分别交于点,点.因为分别是,的中点,所以,
所以,是平面与平面的交线.由是等边三角形,是的重心,
知点,点分别是线段,的中点.平面,平面,所以,
又,平面,,则平面,所以平面,
又平面,于是,,为平面与平面所成二面角的平面角.
由等边三角形的边长为,可得,,,,
,在中,由余弦定理,得,
所以平面与平面夹角的余弦值为.
【例3-2】 (2023·青海·海东市第一中学)如图,在四棱锥P-ABCD中,平面平面ABCD,为等边三角形,,,M是棱上一点,且.
(1)求证:平面MBD;
(2)求二面角M-BD-C的余弦值.
【答案】(1)证明见解析(2)
【解析】(1)连接AC,记AC与BD的交点为H,连接MH.
由,得,,又,则,
∴,又平面MBD,平面MBD,
∴平面MBD.
(2)记O为CD的中点,连接PO,BO.
∵为等边三角形,∴,
∵平面平面ABCD,平面平面ABCD=CD,
∴平面ABCD.
以O为原点,OB为x轴,OC为y轴,OP为x轴,建立空间直角坐标系,如下图,
则,,,,,
,.
设平面BDM的法向量,则,
取x=1得,
平面BCD的一个法向量.
设二面角M-BD-C的平面角为θ,则.
∴二面角M-BD-C的余弦值为.
【一隅三反】
1. (2023·天津·高考真题)直三棱柱中,,D为的中点,E为的中点,F为的中点.
(1)求证:平面;
(2)求直线与平面所成角的正弦值;
(3)求平面与平面所成二面角的余弦值.
【答案】(1)证明见解析(2)(3)
【解析】(1)证明:在直三棱柱中,平面,且,则以点为坐标原点,、、所在直线分别为、、轴建立如下图所示的空间直角坐标系,则、、、、、、、、,则,易知平面的一个法向量为,则,故,平面,故平面.
(2)解:,,,设平面的法向量为,则,取,可得,.因此,直线与平面夹角的正弦值为.
(3)解:,,设平面的法向量为,则,取,可得,则,因此,平面与平面夹角的余弦值为.
2. (2023·江西)如图,在三棱锥中,是边长为2的正三角形,,,D为上靠近A的三等分点.
(1)若,求证:平面平面;
(2)当三棱锥的体积最大时,求二面角的余弦值.
【答案】(1)证明见解析(2)
【解析】(1)证明:因为是边长为2的正三角形,所以,,又,所以,从而.因为,,所以.又因为D为上靠近A的三等分点,所以,在中,由余弦定理得.因此,所以.因为,所以平面,又平面,所以平面平面.
解:由题意当三棱锥的体积最大时,有平面平面.取的中点O,连接,,则,平面平面,平面,从而平面,又,为的中点,所以;以O点为原点,以为轴正方向,建立如图所示的空间直角坐标系,则,,,,从而,,,设平面的法向量为,则从而,取,则.设平面的法向量为,则从而,取,则.,由图可知二面角为锐角,所以二面角的余弦值为.
3. (2023·广西玉林·模拟预测(理))如图,在直三棱柱 中,D,E别是棱、上的点,,.
(1)求证:平面平面;
(2)若直线与平面ABC所成的角为,且,求二面角的大小.
【答案】(1)证明见解析(2)
【解析】(1)取中点,AB中点O,连交于F,连,,则,∵,∴,∴是平行四边形,∴,∵,∴.又在直三棱柱中,平面,平面,∴,平面,结合,∴平面,∴平面,又平面,∴平面平面.
由(1)知,OC、OB、两两垂直,建立如图空间直角坐标系,取上一点M,使,连AM,则,又平面ABC,与平面ABC所成角为,∴,∴,不妨设,则,,,,∴,,,,,,,.设平面的一个法向量为,则,∴,,取,得,平面的一个法向量,,∴二面角的平面角的正弦值为.
考点四 空间角的综合运用
【例4】 (2023·重庆南开中学)(多选)已知正四棱锥的侧面是边长为6的正三角形,点M在棱PD上,且,点Q在底面及其边界上运动,且面,则下列说法正确的是( )
A.点Q的轨迹为线段
B.与CD所成角的范围为
C.的最小值为
D.二面角的正切值为
【答案】ACD
【解析】对于A,取点,,使得,,连接,,如图,
由线段成比例可得,平面,平面,
所以平面,同理可得平面,
又平面,,所以平面平面,
故当点时,总有面,所以点Q的轨迹为线段,故A正确;
对于B,由知与CD所成角即为与NE所成角,在中,,由余弦定理可得,由,可知,即运动到点时,异面直线所成的角小于,故B错误;
对于C,当时,最小,此时,故C正确;
对于D,二面角即平面与底面所成的锐角,连接相交于,连接,取点H,使得,连接MH,过H作于G,连接,如图,
由正四棱锥可知,面,由,知,
,由可得,
,面,,又,,平面,,即为二面角的平面角,,故D正确.
故选:ACD
【一隅三反】
1. (2023·湖南·长郡中学模拟预测)(多选)已知正方体的边长为2,M为的中点,P为侧面上的动点,且满足平面,则下列结论正确的是( )
A.B.平面
C.与所成角的余弦值为D.动点P的轨迹长为
【答案】BCD
【解析】如图建立空间直角坐标系,设正方体棱长为2,
则,
所以,
由平面,得,即,
化简可得:,
所以动点P在直线上,
对于选项A:,所以与不垂直,所以A选项错误;
对于选项B:平面平面,所以平面,B选项正确;
对于选项C:,C选项正确;
对于选项D:动点P在直线上,且P为侧面上的动点,则P在线段上,,所以,D选项正确;
故选:BCD.
2. (2023·福建·三明一中模拟预测)已知正方体中,,点E为平面内的动点,设直线与平面所成的角为,若,则点E的轨迹所围成的面积为___________.
【答案】
【解析】如图所示,连接交平面于,连接,
由题意可知平面,
所以是与平面所成的角,
所以=.
由可得,即.
在四面体中,, ,
所以四面体为正三棱锥,为的重心,
如图所示:
所以解得 ,,
又因为,
所以 ,
即在平面内的轨迹是以O为圆心,半径为1的圆,
所以.
故答案为:.
相关试卷
这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.5 外接球(精讲)(提升版)(原卷版+解析版),共31页。试卷主要包含了汉堡模型,墙角模型,斗笠模型,麻花模型,L模型,怀表模型,矩形模型,内切球等内容,欢迎下载使用。
这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.4 空间距离(精讲)(提升版)(原卷版+解析版),共30页。试卷主要包含了点线距,点面距,线线距,线面距,面面距等内容,欢迎下载使用。
这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 5.2 三角公式的运用(精讲)(提升版)(原卷版+解析版),共19页。试卷主要包含了公式的基本运用,角的拼凑,恒等变化,三角公式与其他知识综合运用等内容,欢迎下载使用。









