2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.5 外接球（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 7.5 外接球（精讲）（提升版）（原卷版+解析版），共31页。试卷主要包含了汉堡模型，墙角模型，斗笠模型，麻花模型，L模型，怀表模型，矩形模型，内切球等内容，欢迎下载使用。


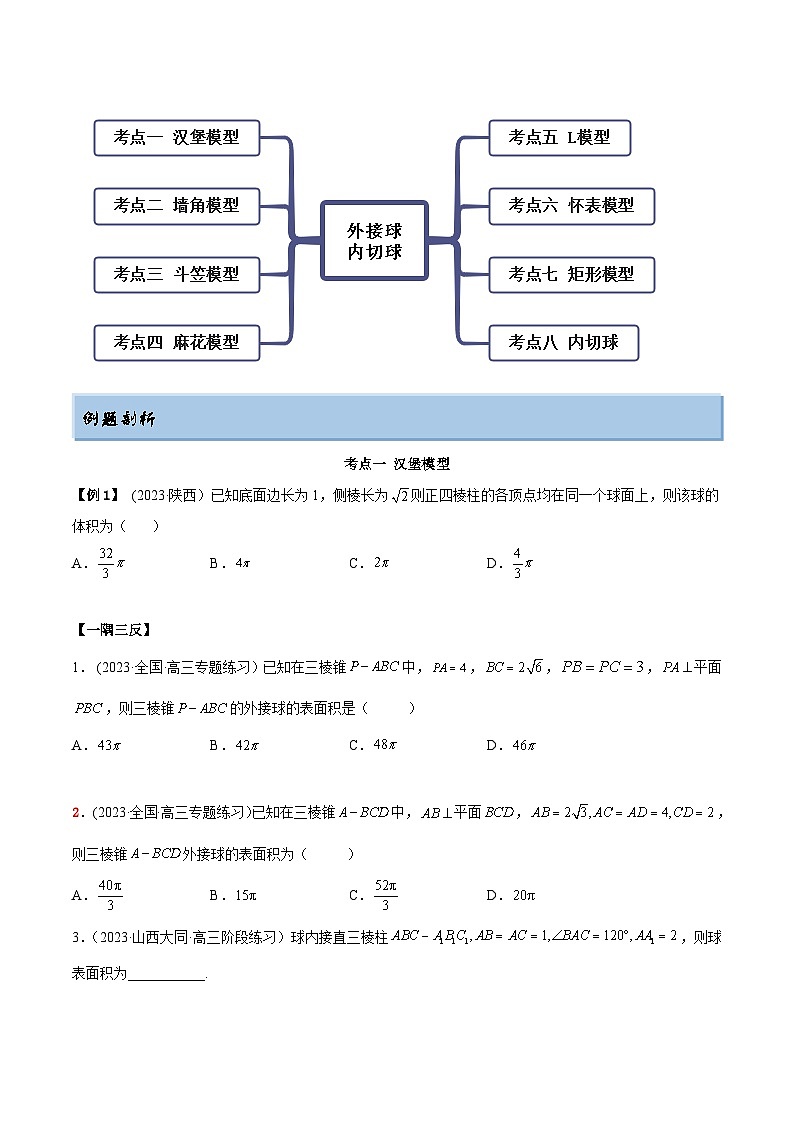
考点呈现
例题剖析
考点一 汉堡模型
【例1】 (2023·陕西）已知底面边长为1，侧棱长为则正四棱柱的各顶点均在同一个球面上，则该球的体积为（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习）已知在三棱锥中，，，，平面，则三棱锥的外接球的表面积是（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）已知在三棱锥中，平面，，则三棱锥外接球的表面积为（ ）
A．B．C．D．
3．（2023·山西大同·高三阶段练习）球内接直三棱柱，则球表面积为___________.
考点二 墙角模型
【例2】 (2023·全国·高三专题练习）长方体的长，宽，高分别为3，，1，其顶点都在球O的球面上，则球O的体积为（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习）已知四棱锥P-ABCD中，平面ABCD，底面ABCD是矩形，，若四棱锥P-ABCD外接球的表面积为，则四棱锥P-ABCD的体积为（ ）
A．3B．2C．D．1
2． (2023·全国·高三专题练习）已知三棱锥中，，底面，，，则该三棱锥的外接球的体积为（ ）
A．B．C．D．
3． (2023·海原县）已知三棱锥的所有顶点都在球的球面上，且平面，，，，则球的表面积为___________.
考点三 斗笠模型
【例3】（2023·全国·高三专题练习）已知三棱锥的四个顶点都在球的球面上是边长为的正三角形，则球的表面积等于（ ）
A．B．C．D．
【一隅三反】
1 (2023·全国·高三专题练习）已知圆台的母线长为2，母线与轴的夹角为60°，且上、下底面的面积之比为1：4，则该圆台外接球的表面积为（ ）
A．B．C．D．
2． (2023·湖北武汉·高三开学考试）已知正三棱锥的各顶点都在同一球面上，若该球的表面积为，则该正三棱锥体积的最大值为___________.
3． (2023·江西）正三棱锥P－ABC底面边长为2，M为AB的中点，且PM⊥PC，则三棱锥P－ABC外接球的体积为（ ）
A．B．C．D．
考点四 麻花模型
【例4】 (2023·全国·高三专题练习）如图，在三棱锥中，，，，则三棱锥外接球的体积为（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习）在三棱锥中，，，，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）在三棱锥A-BCD中，，，二面角A-BD-C是钝角.若三棱锥A-BCD的体积为2，则A-BCD的外接球的表面积是（ ）
A．12πB．13πC．D．

考点五 L模型
【例5】 (2023·全国·高三专题练习）在三棱锥中，平面平面，，，则该三棱锥外接球的表面积是（ ）
A．B．C．D．
【一隅三反】
1 (2023·江西高三）在三棱锥中，是等边三角形，平面平面，，则三棱锥的外接球体积为（ ）
A．B．C．D．
2． (2023·四川雅安市）在四面体ABCD中，已知平面平面，且，其外接球表面积为 （ ）
A．B．C．D．
3．（2023·重庆九龙坡区）在三棱锥中，平面平面，，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
考点六 怀表模型
【例6】 (2023·全国·高三专题练习）在边长为6的菱形ABCD中，，现将沿BD折起到的位置，当三棱锥的体积最大时，三棱锥的外接球的表面积为（ ）
A．60πB．45πC．30πD．20π
【一隅三反】
1． (2023·全国·高三专题练习）在三棱锥中，是边长为的等边三角形，，二面角是150°，则三棱锥外接球的表面积是（ ）
A．B．
C．D．
2． (2023·全国·高三专题练习）在三棱锥中，为等腰直角三角形，，为正三角形，且二面角的平面角为，则三棱锥的外接球表面积为（ ）
A．B．C．D．
考点七 矩形模型
【例7】 (2023·湖北襄阳市）若矩形ABCD的面积是4，沿对角线AC将矩形ABCD折成一个大小是60°的二面角B-AC-D，则四面体ABCD的外接球的体积最小值为（ ）
A．B．C．D．
【一隅三反】
1． (2023.江西）在矩形中，，沿对角线进行翻折，则三棱锥外接球的表面积为（ ）
A．B．C．D．
2． (2023·天津河）将长、宽分别为和的长方形沿对角线折成直二面角，得到四面体，则四面体的外接球的表面积为（ ）
A．B．C．D．
3． (2023·四川）中国古代数学家刘徽所注释的《九章算术》中，称四个面均为直角三角形的四面体为“鳖臑”.如图所示的鳖臑中，面，，若，，且顶点均在球上，则球的表面积为______.
考点八 内切球
【例8】 (2023·全国·高三专题练习）如图，在三棱锥中，，，若三棱锥的内切球的表面积为，则此三棱锥的体积为（ ）
A．B．C．D．
【一隅三反】
1． (2023·江西·高三阶段练习（理））在正三棱锥中，，分别是，的中点，且，，则正三棱锥的内切球的表面积为（ ）
A．B．
C．D．
2． (2023·全国·高三专题练习）在三棱锥中，平面，且，若球在三棱锥的内部且与四个面都相切（称球为三棱锥的内切球），则球的表面积为（ ）
A．B．C．D．
3. (2023黑龙江）如图，在四棱锥中，是正方形的中心，底面，，，则四棱锥内切球的体积为（ ）
A．B．C．D．
7.5 外接球（精讲）（提升版）
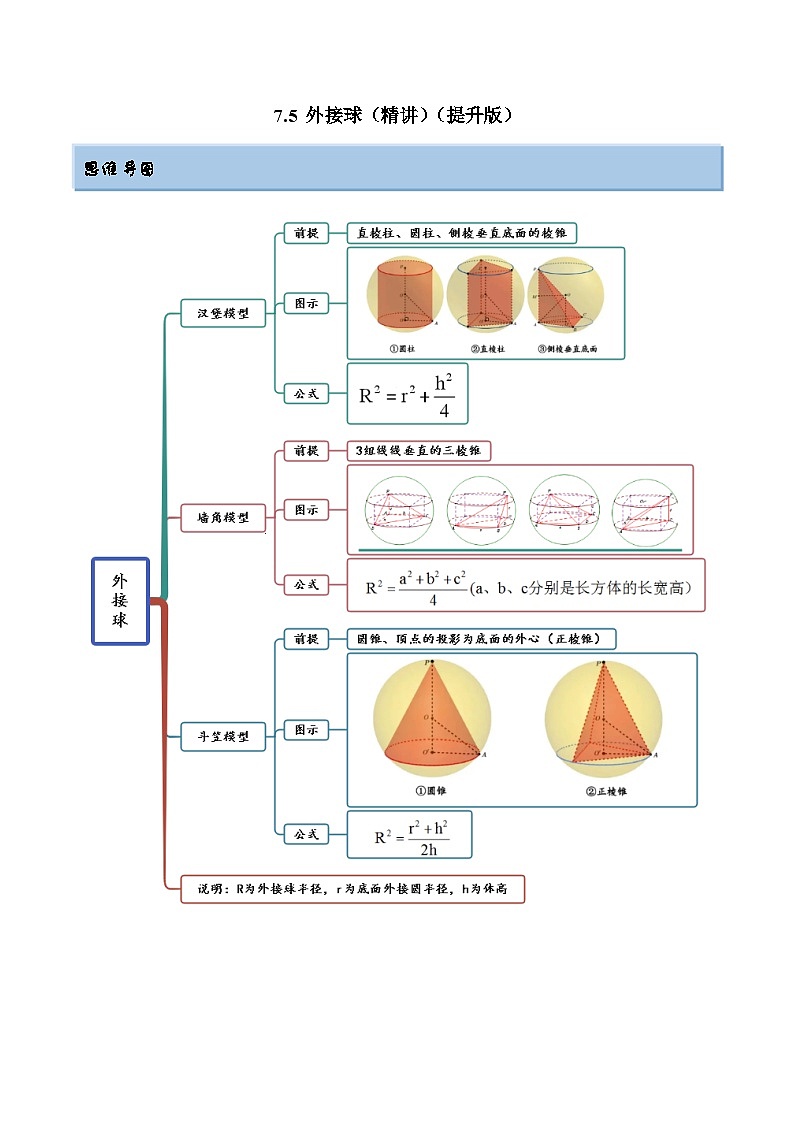
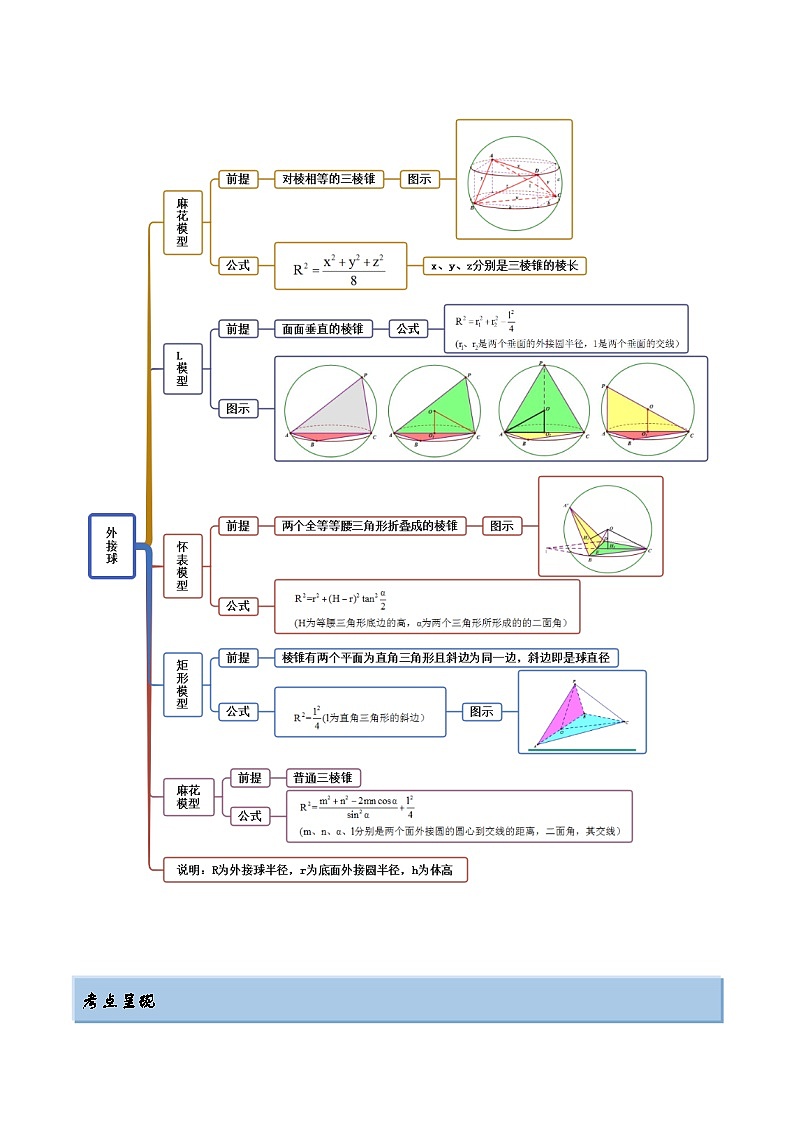
思维导图
考点呈现
例题剖析
考点一 汉堡模型
【例1】 (2023·陕西）已知底面边长为1，侧棱长为则正四棱柱的各顶点均在同一个球面上，则该球的体积为（ ）
A．B．C．D．
【答案】D
【解析】由题可知，正四棱柱的体对角线即为外接球的直径，故，
解得，故球的体积为：.故选：D.
【一隅三反】
1． (2023·全国·高三专题练习）已知在三棱锥中，，，，平面，则三棱锥的外接球的表面积是（ ）
A．B．C．D．
【答案】A
【解析】
在中，由余弦定理得：，
，
外接圆半径，又平面，
三棱锥的外接球半径，
则三棱锥的外接球的表面积.
故选：A.
2． (2023·全国·高三专题练习）已知在三棱锥中，平面，，则三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】C
【解析】因平面，平面，则，而，
则，三棱锥的外接球截平面所得小圆圆心是正的中心，，
连，则平面，取线段的中点，则球的球心在过E垂直于直线的垂面上，连，如图，则四边形是矩形，，因此，球的半径有：，
所以三棱锥外接球的表面积.故选：C
3．（2023·山西大同·高三阶段练习）球内接直三棱柱，则球表面积为___________.
【答案】
【解析】设三角形ABC和三角形的外心分别为D，E．可知其外接球的球心O是线段DE的中点，连结OC，CD，设外接球的半径为R，三角形ABC的外接圆的半径r，可得，由正弦定理得，，
而在三角形OCD中，可知，
即，因此三棱柱外接球的表面积为．
故答案为：
考点二 墙角模型
【例2】 (2023·全国·高三专题练习）长方体的长，宽，高分别为3，，1，其顶点都在球O的球面上，则球O的体积为（ ）
A．B．C．D．
【答案】A
【解析】球O的半径为，∴体积．故选：A
【一隅三反】
1． (2023·全国·高三专题练习）已知四棱锥P-ABCD中，平面ABCD，底面ABCD是矩形，，若四棱锥P-ABCD外接球的表面积为，则四棱锥P-ABCD的体积为（ ）
A．3B．2C．D．1
【答案】D
【解析】设四棱锥P-ABCD外接球的半径为R，则，即．
由题意，易知，得，
设，得，解得，
所以四棱锥P-ABCD的体积为．
故选：D
2． (2023·全国·高三专题练习）已知三棱锥中，，底面，，，则该三棱锥的外接球的体积为（ ）
A．B．C．D．
【答案】B
【解析】解：如图所示，将三棱锥放在长、宽、高分别为，，的长方体中，
则三棱锥的外接球即为该长方本的外接球，
所以外接球的直径，
∴该球的体积为.故选：B
3． (2023·海原县）已知三棱锥的所有顶点都在球的球面上，且平面，，，，则球的表面积为___________.
【答案】
【解析】平面，平面，，，
又，，，
，，则可将三棱锥放入如下图所示的长方体中，
则长方体的外接球即为三棱锥的外接球，
球的半径，
球的表面积.故答案为：.
考点三 斗笠模型
【例3】（2023·全国·高三专题练习）已知三棱锥的四个顶点都在球的球面上是边长为的正三角形，则球的表面积等于（ ）
A．B．C．D．
【答案】B
【解析】已知三棱锥的四个顶点都在球O的球面上，是边长为的正三角形，如图所示：
取BC的中点D，点H为底面的中心，所以
设外接球的半径为R，所以，
利用勾股定理可得，解得
则球的表面积为
故选：B.
【一隅三反】
1 (2023·全国·高三专题练习）已知圆台的母线长为2，母线与轴的夹角为60°，且上、下底面的面积之比为1：4，则该圆台外接球的表面积为（ ）
A．B．C．D．
【答案】C
【解析】
圆台上、下底面的面积之比为1：4，则半径比为1：2，设圆台上、下底面半径为，因母线与轴的夹角为60°，可得圆台高为1，则；
设圆台外接球的半径为，球心到下底面的距离为，易得圆台两底面在球心同侧，则，且，解得，则该圆台外接球的表面积为.故选：C.
2． (2023·湖北武汉·高三开学考试）已知正三棱锥的各顶点都在同一球面上，若该球的表面积为，则该正三棱锥体积的最大值为___________.
【答案】
【解析】因为，所以正三棱锥外接球半径，
正三棱锥如图所示，设外接球圆心为，过向底面作垂线垂足为，
因为是正三棱锥，所以是的中心，
所以，,
又因为，所以
，
所以，
令，
解得
所以在递增，在递减，
故当时，取最大值，.
故答案为：.
3． (2023·江西）正三棱锥P－ABC底面边长为2，M为AB的中点，且PM⊥PC，则三棱锥P－ABC外接球的体积为（ ）
A．B．C．D．
【答案】C
【解析】
由图，设，则，而，
因为PM⊥PC，所以由勾股定理得即解得，
由对称性可知：三棱锥P－ABC外接球的球心在三棱锥P－ABC的高PD上，
假设为O点，则，因为,所以，
又由于点D是三角形ABC的外心，且三角形ABC为等边三角形，所以,
在三角形ODC中，由勾股定理得,即， 解得，
所以三棱锥P－ABC外接球的体积为.故选：C
考点四 麻花模型
【例4】 (2023·全国·高三专题练习）如图，在三棱锥中，，，，则三棱锥外接球的体积为（ ）
A．B．C．D．
【答案】C
【解析】由题意，，，，将三棱锥放到长方体中，可得长方体的三条对角线分别为，2，，
设长方体的长、宽、高分别为，
则，，，
解得，，．
所以三棱锥外接球的半径．
三棱锥外接球的体积．故选：C
【一隅三反】
1． (2023·全国·高三专题练习）在三棱锥中，，，，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】A
【解析】三棱锥中，，，，
构造长方体，使得面上的对角线长分别为4，5，，则长方体的对角线长等于三棱锥外接球的直径，如图，
设长方体的棱长分别为，，，则，，，则，
因此三棱锥外接球的直径为，所以三棱锥外接球的表面积为．
故选：A
2． (2023·全国·高三专题练习）在三棱锥A-BCD中，，，二面角A-BD-C是钝角.若三棱锥A-BCD的体积为2，则A-BCD的外接球的表面积是（ ）
A．12πB．13πC．D．
【答案】B
【解析】如图1，取中点，连接，则，，又，平面，所以平面，
，所以，
又，
，，
又由，，知为二面角的平面角，此角为钝角，
所以，
所以，
因此四面体可以放置在一个长方体中，四面体的六条棱是长方体的六个面对角线，如图2，
此长方体的外接球就是四面体的外接球，设长方体的棱长分别为，
则，解得，
所以外接球的直径为，，
球表面积为．
故选：B．

考点五 L模型
【例5】 (2023·全国·高三专题练习）在三棱锥中，平面平面，，，则该三棱锥外接球的表面积是（ ）
A．B．C．D．
【答案】B
【解析】如图所示：其中D为AB的中点，O为外接圆的圆心，，
∴O在CD上，且，
．
，D为AB的中点，
，
∵平面平面ABC，平面平面，平面ABC，
平面PAB．又DA，DB，平面PAB，
，，．
在中，，D为AB的中点，
．
．
∴O即为三棱锥外接球的球心，且外接球半径，
∴该三棱锥外接球的表面积．
故选：B
【一隅三反】
1 (2023·江西高三）在三棱锥中，是等边三角形，平面平面，，则三棱锥的外接球体积为（ ）
A．B．C．D．
【答案】C
【解析】中，，
所以，，
设是中点，则是外心，又是等边三角形，所以，
而平面平面，平面平面，平面，所以平面，所以的外心即中三棱锥外接球的球心，
所以球半径，球体积为．故选：C．
2． (2023·四川雅安市）在四面体ABCD中，已知平面平面，且，其外接球表面积为 （ ）
A．B．C．D．
【答案】B
【解析】四面体ABCD中，取AB的中点E，连CE，DE，如图：
因，则，有平面CDE，
所以平面CDE⊥平面ABC，平面CDE⊥平面ABD，令正△ABD中心为O2，正△ABC中心为O1，
在平面CDE内分别过O1，O2作直线CE，DE的垂线，两线交于点O，则有O1O⊥平面ABC，平面O2O⊥平面ABD，
由球的截面小圆性质知，四面体ABCD外接球球心在直线O1O和直线O2O上，即点O是球心，连OA，O1A，OA即为球O的半径，
因平面平面，则，而，
即有四边形OO1EO2是正方形，则，
中，，则，
所求外接球的表面积.故选：B
3．（2023·重庆九龙坡区）在三棱锥中，平面平面，，则三棱锥的外接球的表面积为（ ）
A．B．C．D．
【答案】C
【解析】如图，取中点，中点，连接，是等边三角形，则
因为平面平面，平面平面，平面，所以平面，又平面，所以，
过作平面，则，
因为，所以三棱锥的外接球的球心在上，设球心为，连接，设外接球半径为，
由已知，，，，
在直角梯形中，，，，
所以球表面积为．故选：C．
考点六 怀表模型
【例6】 (2023·全国·高三专题练习）在边长为6的菱形ABCD中，，现将沿BD折起到的位置，当三棱锥的体积最大时，三棱锥的外接球的表面积为（ ）
A．60πB．45πC．30πD．20π
【答案】A
【解析】当三棱锥的体积最大值时，平面平面，如图，
取的中点为，连接，则.
设分别为，外接圆的圆心，
为三棱锥的外接球的球心，
则在上，在上，且,
且平面，平面.
平面平面，平面平面，
平面，
平面，，同理
四边形为平行四边形
平面，平面
，即四边形为矩形.


外接球半径
外接球的表面积为
故选：A.
【一隅三反】
1． (2023·全国·高三专题练习）在三棱锥中，是边长为的等边三角形，，二面角是150°，则三棱锥外接球的表面积是（ ）
A．B．
C．D．
【答案】A
【解析】如图，作平面ABC，垂足为E，连接BE，记，连接PD.
由题意可得D为AC的中点.
在中，，D为AC的中点，
因为，所以，则.
因为二面角是150°，所以，
所以，.
因为是边长为的等边三角形，且D为AC的中点，所以.
设为外接圆的圆心，则.
设三棱锥外接球的球心为O，
因为，所以O在平面ABC下方，
连接，OB，OP，作，垂足为H，
则，.
设三棱锥外接球的半径为，
，即，解得，
故三棱锥外接球的表面积是.
故选：A.
2． (2023·全国·高三专题练习）在三棱锥中，为等腰直角三角形，，为正三角形，且二面角的平面角为，则三棱锥的外接球表面积为（ ）
A．B．C．D．
【答案】C
【解析】如图所示，为直角三角形，又，
所以，
因为为正三角形，所以，
连接，为的中点，E为中点，
则，所以为二面角的平面角
所以．
因为为直角三角形，E为中点，
所以点为的外接圆的圆心，
设G为的中心，则G为的外接圆圆心．过E作面的垂线，过G作面的垂线，设两垂线交于O．
则O即为三棱锥的外接球球心．设与交于点H，
，所以,，
∴．所以，故选：C.
考点七 矩形模型
【例7】 (2023·湖北襄阳市）若矩形ABCD的面积是4，沿对角线AC将矩形ABCD折成一个大小是60°的二面角B-AC-D，则四面体ABCD的外接球的体积最小值为（ ）
A．B．C．D．
【答案】B
【解析】因为球心到四个顶点的距两相等,所以球心在对角线上,且半径为，
设矩形的的长力x,宽为y则，所以，
又，由基本不等式知: ，当且仅当 ，即时，等号成立，
，故选：B
【一隅三反】
1． (2023.江西）在矩形中，，沿对角线进行翻折，则三棱锥外接球的表面积为（ ）
A．B．C．D．
【答案】D
【解析】因为在翻折过程中，始终不变，
所以的中点到，，，四点的距离始终相等，三棱锥外接球的直径为，
所以外接球的表面积为，故选：D
2． (2023·天津河）将长、宽分别为和的长方形沿对角线折成直二面角，得到四面体，则四面体的外接球的表面积为（ ）
A．B．C．D．
【答案】A
【解析】取的中点，连接、，如下图所示：
由题意，
因为，为的中点，所以，，
所以，为四面体的外接球的球心，且球的半径为，
因此，四面体的外接球的表面积为.故选：A.
3． (2023·四川）中国古代数学家刘徽所注释的《九章算术》中，称四个面均为直角三角形的四面体为“鳖臑”.如图所示的鳖臑中，面，，若，，且顶点均在球上，则球的表面积为______.
【答案】
【解析】由题意可知：球为鳖臑的外接球，
面，面，，，
又，面，，面，
又面，；
取中点，连接，
，，同理可知：，
点与球的球心重合，球的半径，
球的表面积.故答案为：.
考点八 内切球
【例8】 (2023·全国·高三专题练习）如图，在三棱锥中，，，若三棱锥的内切球的表面积为，则此三棱锥的体积为（ ）
A．B．C．D．
【答案】D
【解析】连接，并延长交底面于点，连接，并延长交于，
在三棱锥中，，，
三棱锥是正四面体，是的中心，平面，
三棱锥的内切球的表面积为，
，解得球的半径，
设，则，，
，
，，，解得，，
此三棱锥的体积为.故选：D.
【一隅三反】
1． (2023·江西·高三阶段练习（理））在正三棱锥中，，分别是，的中点，且，，则正三棱锥的内切球的表面积为（ ）
A．B．
C．D．
【答案】D
【解析】设点是点在底面上的射影，则平面，平面，
所以，由三棱锥为正三棱锥可得，点为底面的中心，
所以，又，
所以平面，平面，
所以，
因为，分别是，的中点，
所以，因为，
所以，又，
所以平面，又，平面，
所以，，又三棱锥是正三棱锥，
所以三条侧棱两两互相垂直，因为，
所以，
所以，
所以该三棱锥的表面积，
设内切球的半径为，又该三棱锥的体积，
所以，
所以此内切球的表面积为.
故选：D.
2． (2023·全国·高三专题练习）在三棱锥中，平面，且，若球在三棱锥的内部且与四个面都相切（称球为三棱锥的内切球），则球的表面积为（ ）
A．B．C．D．
【答案】A
【解析】解：因为平面，平面，平面，平面，
所以，，，
又，
所以平面，所以，
所以均为直角三角形，
设球的半径为r，则，
而，，
所以，解得，
所以球的表面积为，
故选：A.
3. (2023黑龙江）如图，在四棱锥中，是正方形的中心，底面，，，则四棱锥内切球的体积为（ ）
A．B．C．D．
【答案】B
【解析】由题可知,该几何体的底面是边长为2的正方形，侧棱长都为，连接.
底面，.
，
，
，.
设四棱锥的内切球的半径为，球心为，
由，
得，
即，解得，
故四棱锥内切球的体积为.故选：B.