2024年新高考数学专用第一轮复习讲义一隅三反提升卷 9.3 双曲线（精讲）（提升版）（原卷版+解析版）

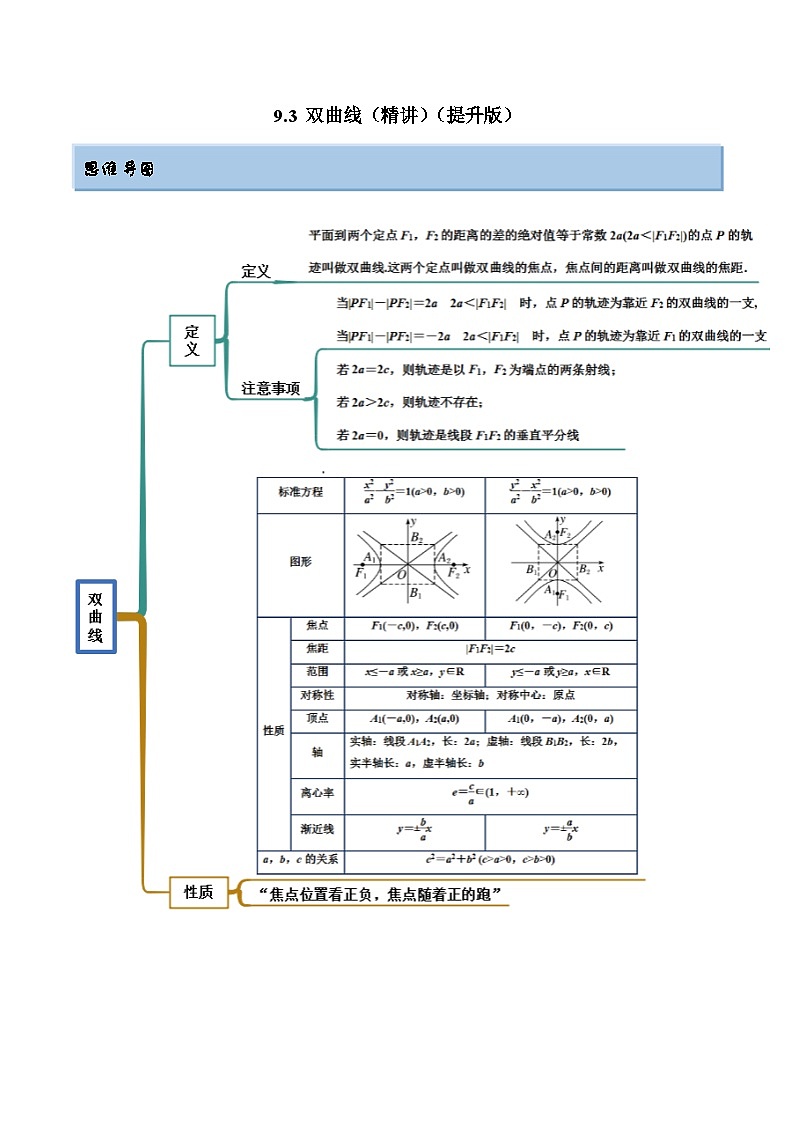
这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 9.3 双曲线（精讲）（提升版）（原卷版+解析版），共27页。试卷主要包含了双曲线的定义及应用，双曲线的离心率及渐近线，双曲线的标准方程，直线与双曲线的位置关系，弦长与中点弦等内容，欢迎下载使用。


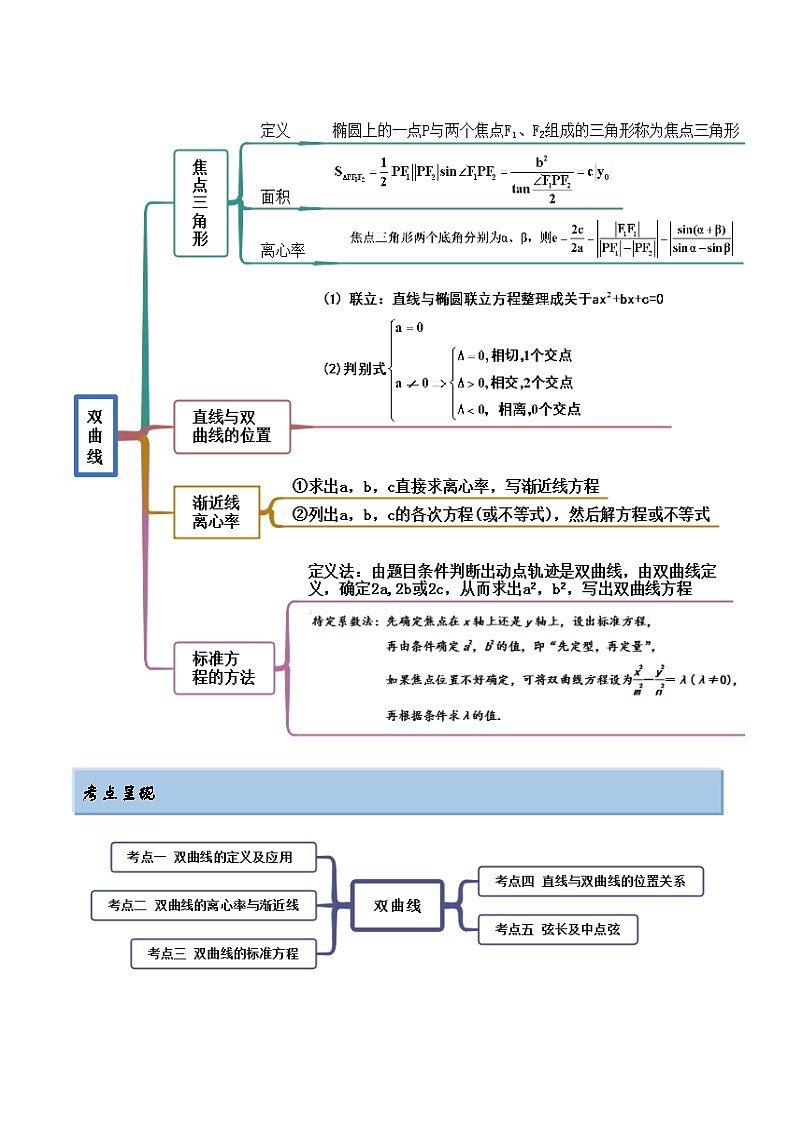
考点呈现
例题剖析
考点一 双曲线的定义及应用
【例1-1】 (2023内江期末）“”是“为双曲线”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【例1-2】 (2023·成都模拟）设，是双曲线的左，右焦点，点P在双曲线C的右支上，当时，面积为（ ）．
A．B．C．D．
【例1-3】 (2023·邯郸模拟）已知､是双曲线的左､右焦点，点为双曲线右支上一点，且在以为直径的圆上，若，则（ ）
A．B．C．D．
【例1-3】 (2023·岳普湖模拟）已知双曲线，F1，F2是双曲线的左右两个焦点，P在双曲线上且在第一象限，圆M是△F1PF2的内切圆.则M的横坐标为 ，若F1到圆M上点的最大距离为，则△F1PF2的面积为 .
【一隅三反】
1． (2023·潮州二模）若点P是双曲线上一点，，分别为的左、右焦点，则“”是“”的（ ）．
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
2． (2023常州期中）已知双曲线的右焦点为，为双曲线左支上一点，点，则周长的最小值为（ ）
A． B． C． D．
3．（202郫都期中）双曲线 的两个焦点为 ， ，双曲线上一点 到 的距离为11，则点 到 的距离为（ ）
A．1B．21C．1或21D．2或21
4 (2023广东）已知，分别是双曲线的左､右焦点，若P是双曲线左支上的点，且.则的面积为（ ）
A．8B．C．16D．
考点二 双曲线的离心率及渐近线
【例2-1】 (2023高三下·安徽期中）已知，是双曲线的左､右焦点，点P在双曲线的右支上，且，，则双曲线C的离心率是（ ）
A．B．C．D．
【例2-2】 (2023·河南模拟）已知双曲线的左、右焦点分别为，，P是双曲线上一点，且（为坐标原点），若内切圆的半径为，则C的离心率是（ ）
A．B．C．D．
【例2-3】 (2023·德阳三模）设双曲线的右焦点是F，左､右顶点分别是，过作轴的垂线与双曲线交于两点，若，则该双曲线的渐近线方程为（ ）
A．B．C．D．
【一隅三反】
1． (2023·重庆市模拟）已知双曲线C：的左右焦点分别为，，点在轴上，为等边三角形，且线段的中点恰在双曲线C上，则双曲线C的离心率为（ ）
A．B．2C．D．
2． (2023·保定模拟）已知F为双曲线的右焦点，A为双曲线C上一点，直线轴，与双曲线C的一条渐近线交于B，若，则C的离心率（ ）
A．B．C．D．2
3． (2023·石嘴山模拟）已知双曲线的左、右焦点分别为，P为双由线C上的一点，若线段与y轴的交点M恰好是线段的中点，，其中，O为坐标原点，则双曲线C的渐近线的方程是（ ）
A．B．C．D．
考点三 双曲线的标准方程
【例3-1】 (2023梧州期末）设双曲线C：（，）的左焦点为F，直线过点F且与双曲线C在第二象限的交点为P，，其中O为坐标原点，则双曲线C的方程为（ ）
A．B．C．D．
【例3-2】．（202合肥期末）已知点分别是等轴双曲线的左、右焦点，为坐标原点，点在双曲线上，，的面积为8，则双曲线的方程为（ ）
A．B．C．D．
【一隅三反】
2． (2023·和平模拟）已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为（ ）
A．B．
C．D．
2．（2022宁波期末）已知双曲线与双曲线有相同的渐近线， 且它们的离心率不相同， 则下列方程中有可能为双曲线的标准方程的是（ ）
A．B．C．D．
3． (2023·湖北模拟）在平面直角坐标系中，已知圆：，点，是圆上任意一点，线段的垂直平分线与直线相交于点，设点的轨迹为曲线，则曲线的方程为 .
4． (2023·广州模拟）写出一个同时满足下列性质①②③的双曲线方程 ．
①中心在原点，焦点在y轴上；②一条渐近线方程为﹔③焦距大于10
考点四 直线与双曲线的位置关系
【例4-1】 (2023·全国·高三专题练习）过且与双曲线有且只有一个公共点的直线有（ ）
A．1条B．2条C．3条D．4条
【例4-2】 (2023·山东）已知直线l的方程为，双曲线C的方程为.若直线l与双曲线C的右支相交于不同的两点，则实数k的取值范围是（ ）
A．B．C．D．
【一隅三反】
1． (2023·上海）若过点的直线与双曲线:的右支相交于不同两点，则直线斜率的取值范围为（ ）
A．B．C．D．
2．（2023·全国·高三专题练习（理））若在区间内随机取一个实数，则直线与双曲线的左、右两支各有一个交点的概率为（ ）
A．B．C．D．
2． (2023·安徽 ）直线与双曲线没有公共点，则斜率k的取值范围是（ ）
A．B．
C．D．
考点五 弦长与中点弦
【例5】（2022云南）已知双曲线，过点的直线l与双曲线C交于M､N两点，若P为线段MN的中点，则弦长|MN|等于（ ）
A．B．C．D．
【一隅三反】
1． (2023·山西）过双曲线的右焦点作倾斜角为30°的直线l，直线l与双曲线交于不同的两点A，B，则AB的长为______．
2 (2023·湖南岳阳·三模）已知F1，F2分别为双曲线C: 的上、下焦点，过点F2作y轴的垂线交双曲线C于P，Q两点，则△PF1Q的面积为________．
3． (2023·全国·高三专题练习）已知双曲线的左､右焦点分别为过左焦点作斜率为2的直线与双曲线交于A，B两点，P是AB的中点，O为坐标原点，若直线OP的斜率为，则b的值是（ ）
A．2B．C．D．
4． (2023·山东烟台·三模）过双曲线：（，）的焦点且斜率不为0的直线交于A，两点，为中点，若，则的离心率为（ ）
A．B．2C．D．
9.3 双曲线（精讲）（提升版）
思维导图
考点呈现
例题剖析
考点一 双曲线的定义及应用
【例1-1】 (2023内江期末）“”是“为双曲线”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】C
【解析】因为方程表示双曲线，所以，
又当时，方程表示双曲线，
因此“”是“方程表示双曲线”的充要条件.故答案为：C
【例1-2】 (2023·成都模拟）设，是双曲线的左，右焦点，点P在双曲线C的右支上，当时，面积为（ ）．
A．B．C．D．
【答案】B
【解析】∵双曲线，∴，又点P在双曲线C的右支上，，
所以，，即，又，
∴面积为.故答案为：B.
【例1-3】 (2023·邯郸模拟）已知､是双曲线的左､右焦点，点为双曲线右支上一点，且在以为直径的圆上，若，则（ ）
A．B．C．D．
【答案】A
【解析】设，，则.
由双曲线定义知，，又，故，
由于在以为直径的圆上，所以，故有
从而
故答案为：A
【例1-3】 (2023·岳普湖模拟）已知双曲线，F1，F2是双曲线的左右两个焦点，P在双曲线上且在第一象限，圆M是△F1PF2的内切圆.则M的横坐标为 ，若F1到圆M上点的最大距离为，则△F1PF2的面积为 .
【答案】1；
【解析】双曲线的方程为，则.
设圆分别与相切于 ，
根据双曲线的定义可知 ，根据内切圆的性质可知 ①，
而 ②. 由①②得： ，所以 ，
所以直线的方程为 ，即M的横坐标为1
设M的坐标为，则到圆M上点的最大距离为，
即，解得.
设直线的方程为，即.
到直线的距离为，解得 .
所以线的方程为.
由且 在第一象限，解得.
所以.
所以△F1PF2的面积为 .
故答案为：1；
【一隅三反】
1． (2023·潮州二模）若点P是双曲线上一点，，分别为的左、右焦点，则“”是“”的（ ）．
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【解析】由题意可知，，，，
若，则，或1（舍去），
若，，或13，
故“”是“”的充分不必要条件．故答案为：A．
2． (2023常州期中）已知双曲线的右焦点为，为双曲线左支上一点，点，则周长的最小值为（ ）
A． B． C． D．
【答案】B
【解析】曲线右焦点为，周长 要使 周长最小，只需 最小，如图：
当 三点共线时取到，故l=2|AF|+2a= 故答案为：B
3．（202郫都期中）双曲线 的两个焦点为 ， ，双曲线上一点 到 的距离为11，则点 到 的距离为（ ）
A．1B．21C．1或21D．2或21
【答案】B
【解析】不妨设 ， 分别为双曲线的左右焦点，
当P在双曲线的左支时，由双曲线的定义可知， ，又 =11，所以 ，当P在双曲线的右支时，由双曲线的定义可知， ，又 =11，所以 ，又 ，所以右支上不存在满足条件的点P.故答案为：B.
4 (2023广东）已知，分别是双曲线的左､右焦点，若P是双曲线左支上的点，且.则的面积为（ ）
A．8B．C．16D．
【答案】C
【解析】因为P是双曲线左支上的点，所以，
两边平方得，
所以.
在中，由余弦定理得，
所以，所以。故答案为：C
考点二 双曲线的离心率及渐近线
【例2-1】 (2023高三下·安徽期中）已知，是双曲线的左､右焦点，点P在双曲线的右支上，且，，则双曲线C的离心率是（ ）
A．B．C．D．
【答案】C
【解析】由题意可知，， ，
又，，即，
∴，即，∴.故答案为：C.
【例2-2】 (2023·河南模拟）已知双曲线的左、右焦点分别为，，P是双曲线上一点，且（为坐标原点），若内切圆的半径为，则C的离心率是（ ）
A．B．C．D．
【答案】C
【解析】，即为，即为，可得．所以．
根据双曲线的对称性，不妨设点P在第一象限，如图所示，
由题意设的内切圆切三边分别于G，D，E三点，则，，．
又，所以．
设，则，所以，
所以切点D为双曲线的右顶点，所以，
．
在中，由勾股定理得，
整理得，即，解得，
又因为，所以C的离心率为，故答案为：C．
【例2-3】 (2023·德阳三模）设双曲线的右焦点是F，左､右顶点分别是，过作轴的垂线与双曲线交于两点，若，则该双曲线的渐近线方程为（ ）
A．B．C．D．
【答案】C
【解析】设双曲线的半焦距为，则，将，代入双曲线，
得，不妨取，，
又，，∴的斜率分别为：
，，
因为，故，即，即，
所以，故渐近线方程是.
故答案为：C
【一隅三反】
1． (2023·重庆市模拟）已知双曲线C：的左右焦点分别为，，点在轴上，为等边三角形，且线段的中点恰在双曲线C上，则双曲线C的离心率为（ ）
A．B．2C．D．
【答案】C
【解析】如图所示，设 ， ，设线段 的中点为 ，则 在双曲线C的右支上，
又 为等边三角形，所以 ，所以 ，所以
连接 ，则在等边三角形 中 ，且 ，
所以 ，所以 ，即双曲线 的离心率为 .
故答案为：C.
2． (2023·保定模拟）已知F为双曲线的右焦点，A为双曲线C上一点，直线轴，与双曲线C的一条渐近线交于B，若，则C的离心率（ ）
A．B．C．D．2
【答案】B
【解析】由题意得，双曲线的渐近线方程为，
由双曲线的对称性，不妨设均为第一象限点，
当 时，得，所以，
当时，，所以，
因为，所以，所以，得，所以，
所以双曲线的离心率为，故答案为：B
3． (2023·石嘴山模拟）已知双曲线的左、右焦点分别为，P为双由线C上的一点，若线段与y轴的交点M恰好是线段的中点，，其中，O为坐标原点，则双曲线C的渐近线的方程是（ ）
A．B．C．D．
【答案】B
【解析】设双曲线的半焦距为，则点，由题意知轴，
所以点的横坐标为，由双曲线的对称性特点不妨设点P(c，y0)(y0>0)，
所以，解得，所以点，所以点的坐标为(0，b22a)，
所以MF1=(−c，−b22a)，MO=(0，−b22a)，故MF1⋅MO=(−c，−b22a)⋅(0，−b22a)=b44a2=2b2，
所以，所以.所以双曲线的渐近线方程为.故答案为：B.
考点三 双曲线的标准方程
【例3-1】 (2023梧州期末）设双曲线C：（，）的左焦点为F，直线过点F且与双曲线C在第二象限的交点为P，，其中O为坐标原点，则双曲线C的方程为（ ）
A．B．C．D．
【答案】D
【解析】设左焦点F的坐标为，由点F过直线，
所以，解得，
设右焦点为N，连接，，.
由，故三角形为直角三角形，即，
又因为直线斜率为，设直线倾斜角为，则.
又，则，，
由双曲线定义，则，
所以，
所以
所以双曲线C的方程为.
故答案为：D.
【例3-2】．（202合肥期末）已知点分别是等轴双曲线的左、右焦点，为坐标原点，点在双曲线上，，的面积为8，则双曲线的方程为（ ）
A．B．C．D．
【答案】D
【解析】，是的中点，所以，
，则，
，解得，
所以双曲线方程为．
故答案为：D．
【一隅三反】
2． (2023·和平模拟）已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为（ ）
A．B．
C．D．
【答案】D
【解析】因为在双曲线的一条渐近线上， 故可得；
因为抛物线的准线为，故，
又；解得，
故双曲线方程为：.故答案为：D.
2．（2022宁波期末）已知双曲线与双曲线有相同的渐近线， 且它们的离心率不相同， 则下列方程中有可能为双曲线的标准方程的是（ ）
A．B．C．D．
【答案】D
【解析】双曲线中，，则渐近线方程为，离心率为。
对于A，，则离心率，故A错误；
对于B，，则渐近线方程为，故B错误；
对于C，，则离心率，故C错误；
对于D，，则渐近线方程为，离心率，故D正确。
故选：D
3． (2023·湖北模拟）在平面直角坐标系中，已知圆：，点，是圆上任意一点，线段的垂直平分线与直线相交于点，设点的轨迹为曲线，则曲线的方程为 .
【答案】
【解析】因为在线段的垂直平分线上，所以，所以，
由双曲线的定义知点的轨迹是以为焦点，为实轴长的双曲线，则，，得，所以曲线的方程为，故答案为：
4． (2023·广州模拟）写出一个同时满足下列性质①②③的双曲线方程 ．
①中心在原点，焦点在y轴上；②一条渐近线方程为﹔③焦距大于10
【答案】（答案不唯一，写出一个即可）
【解析】由①中心在原点，焦点在y轴上知，可设双曲线方程为：
由②一条渐近线方程为知，，即
由③知，，即，
则可取（此处也可取大于的其他数）
又，，
则同时满足下列性质①②③的一个双曲线方程为：
故答案为：（答案不唯一， 写出一个即可）.
考点四 直线与双曲线的位置关系
【例4-1】 (2023·全国·高三专题练习）过且与双曲线有且只有一个公共点的直线有（ ）
A．1条B．2条C．3条D．4条
【答案】D
【解析】当斜率不存在时，过的直线与双曲线没有公共点；
当斜率存在时，设直线为，联立，得①.
当，即时，①式只有一个解；
当时，则，解得；
综上可知过且与双曲线有且只有一个公共点的直线有4条.故选：D.
【例4-2】 (2023·山东）已知直线l的方程为，双曲线C的方程为.若直线l与双曲线C的右支相交于不同的两点，则实数k的取值范围是（ ）
A．B．C．D．
【答案】D
【解析】联立整理得，因为直线与双曲线的右支交于不同的两点，所以，解得，所以实数k的取值范围为.故选：D.
【一隅三反】
1． (2023·上海）若过点的直线与双曲线:的右支相交于不同两点，则直线斜率的取值范围为（ ）
A．B．C．D．
【答案】D
【解析】由题意可得直线斜率存在，设直线的方程为，
设交点，联立可得，
由题意可得解得：，故选：D．
2．（2023·全国·高三专题练习（理））若在区间内随机取一个实数，则直线与双曲线的左、右两支各有一个交点的概率为（ ）
A．B．C．D．
【答案】B
【解析】双曲线的渐近线斜率为，则，即，故所求概率为，
故选：B.
2． (2023·安徽 ）直线与双曲线没有公共点，则斜率k的取值范围是（ ）
A．B．
C．D．
【答案】A
【解析】联立直线和双曲线：，消去得，
当，即时，此时方程为，解得，此时直线与双曲线有且只有一个交点；
当，此时，
解得或，所以时直线与双曲线无交点；故选：A
考点五 弦长与中点弦
【例5】（2022云南）已知双曲线，过点的直线l与双曲线C交于M､N两点，若P为线段MN的中点，则弦长|MN|等于（ ）
A．B．C．D．
【答案】D
【解析】由题设，直线l的斜率必存在，设过的直线MN为，联立双曲线：
设，则，所以，解得，
则，.弦长|MN|.故选：D.
【一隅三反】
1． (2023·山西）过双曲线的右焦点作倾斜角为30°的直线l，直线l与双曲线交于不同的两点A，B，则AB的长为______．
【答案】
【解析】双曲线的右焦点为，所以直线l的方程为．由，得．设，，则，，
所以．
故答案为：
2 (2023·湖南岳阳·三模）已知F1，F2分别为双曲线C: 的上、下焦点，过点F2作y轴的垂线交双曲线C于P，Q两点，则△PF1Q的面积为________．
【答案】
【解析】双曲线C: 的上、下焦点.
令代入，解得：，所以.
所以，所以△PF1Q的面积为.
故答案为：
3． (2023·全国·高三专题练习）已知双曲线的左､右焦点分别为过左焦点作斜率为2的直线与双曲线交于A，B两点，P是AB的中点，O为坐标原点，若直线OP的斜率为，则b的值是（ ）
A．2B．C．D．
【答案】D
【解析】设、，则，，
两式相减可得，
为线段的中点，，，
，又，，
，即，，
故选：D.
4． (2023·山东烟台·三模）过双曲线：（，）的焦点且斜率不为0的直线交于A，两点，为中点，若，则的离心率为（ ）
A．B．2C．D．
【答案】D
【解析】不妨设过双曲线的焦点且斜率不为0的直线为，令
由，整理得
则，
则，由，可得
则有，即，则双曲线的离心率
故选：D