2024年新高考数学专用第一轮复习讲义一隅三反提升卷 1.1 集合（精讲）（提升版）（原卷版+解析版）

这是一份2024年新高考数学专用第一轮复习讲义一隅三反提升卷 1.1 集合（精讲）（提升版）（原卷版+解析版），共17页。试卷主要包含了集合的基本运算，集合中的参数问题，集合中的新定义，集合与其他知识的综合运用等内容，欢迎下载使用。


考点呈现
例题剖析
考点一 集合的基本运算
【例1-1】 (2023·江苏·苏州中学高三开学考试）已知集合A＝，则A∩B＝（ ）
A．(0，2]B．(0，2)C．(1，2]D．(0，＋∞)
【例1-2】 (2023·河北保定·高三期末）设集合均为非空集合.（ ）
A．若，则 B．若，则
C．若，则 D．若，则
【例1-3】 (2023·全国·高三专题练习）已知集合，，则的元素个数为（ ）
A．2B．1C．0D．无法确定
【一隅三反】
1． (2023·浙江绍兴·高三期末）已知全集，集合，，则（ ）
A．B．C．D．
2． (2023·全国·模拟预测）已知全集，集合，，则图中阴影部分表示的集合为（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）设集合，，，，则（ ）
A．B．C．D．
4． (2023·全国·高三专题练习）已知集合，，则中元素的个数为（ ）
A．3B．2C．1D．0
考点二 集合中的参数问题
【例2-1】 (2023·全国·高三专题练习）集合或，若，则实数的取值范围是（ ）
A．B．C．D．
【例2-2】 (2023·全国·高三专题练习）已知集合，.若，则实数（ ）
A．3B．C．3或D．或1
【例2-3】 (2023·全国·高三专题练习（理））设集合，集合若中恰含有一个整数 ，则实数的取值范围是（ ）
A．B．C．D．
【一隅三反】
1． (2023·全国·高三专题练习（理））设集合，，若，则的取值范围为（ ）
A．B．C．D．
2． (2023·全国·高三专题练习）已知集合，，若，则实数的取值集合为（ ）
A．B．C．D．
3． (2023·全国·高三专题练习）已知集合，.若，则实数（ ）
A．-3B．C．D．3
4． (2023·全国·高三专题练习（理））已知A={-1，2}，B={x|mx+1=0}，若A∪B=A，则实数m的取值所成的集合是（ ）
A．B．
C．D．
考点三 集合中的新定义
【例3】 (2023·全国·高三专题练习）（多选）对任意A，，记，则称为集合A，B的对称差．例如，若，，则，下列命题中，为真命题的是（ ）
A．若A，且，则
B．若A，且，则
C．若A，且，则
D．存在A，，使得
【一隅三反】
1． (2023·贵州）定义集合 且.己知集合，，，则中元素的个数为（ ）
A．3B．4C．5D．6
2． (2023·湖南·雅礼中学一模）已知集合，，定义集合，则中元素的个数为
A．77B．49C．45D．30
3． (2023·全国·高三专题练习）若一个集合是另一个集合的子集，则称两个集合构成“鲸吞”；若两个集合有公共元素，且互不为对方子集，则称两个集合构成“蚕食”，对于集合，，若这两个集合构成“鲸吞”或“蚕食”，则a的取值集合为_____.
4． (2023·全国·高三专题练习）若，则，就称是伙伴关系集合，集合的所有非空子集中，具有伙伴关系的集合个数为_________________.
考点四 集合与其他知识的综合运用
【例4-1】 (2023·全国·高三专题练习）已知是虚数单位，集合（整数集）和的关系韦恩图如图所示，则阴影部分所示的集合的元素共有（ ）
A．3个B．2个C．1个D．无穷个
【例4-2】 (2023·全国·模拟预测（理））已知函数的部分图象如图所示，将函数的图象向右平移个单位长度，得到函数的图象，若集合，集合，则______．
【一隅三反】
1． (2023·上海·高三专题练习）已知互异的复数满足，集合={,},则= （ ）
A．2B．1C．0D．
2． (2023·福建福州·模拟预测）从集合的非空子集中任取两个不同的集合和，若，则不同的取法共有（ ）
A．种B．种C．种D．种
3． (2023·全国·高三专题练习）函数，则集合元素的个数有（ ）
A．个B．个C．个D．个
1.1 集合（精讲）（提升版）
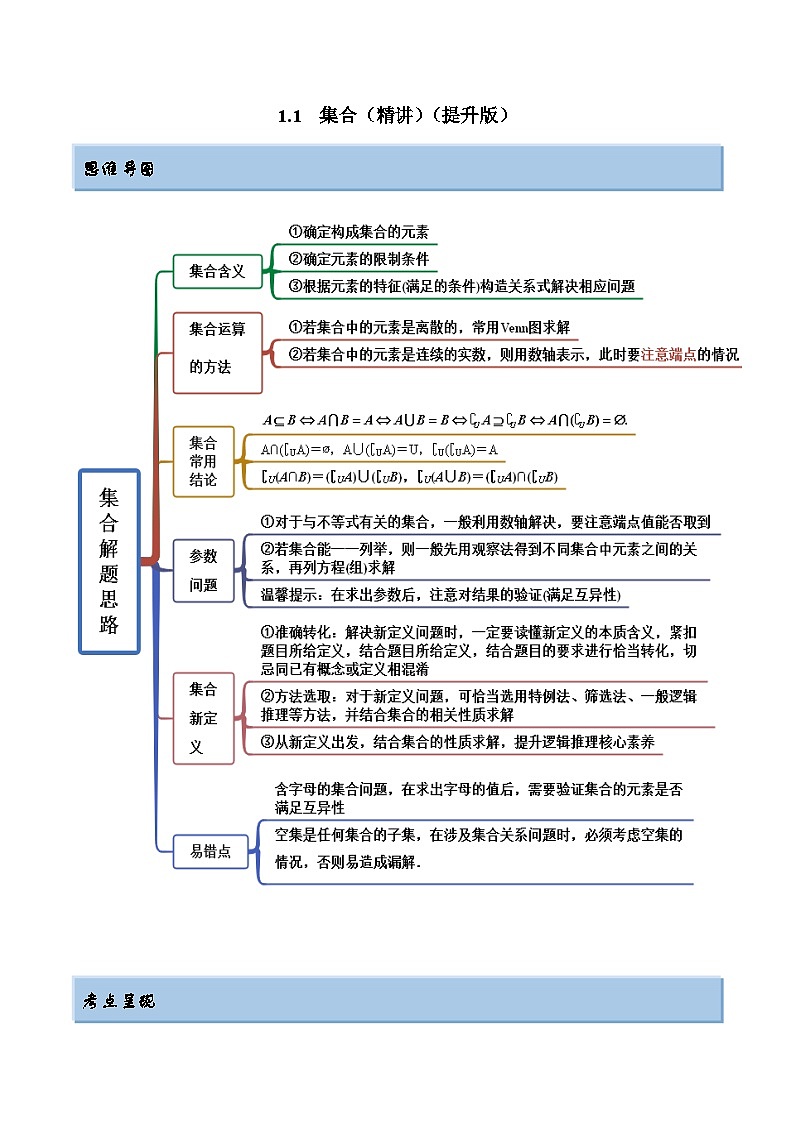
思维导图
考点呈现
例题剖析
考点一 集合的基本运算
【例1-1】 (2023·江苏·苏州中学高三开学考试）已知集合A＝，则A∩B＝（ ）
A．(0，2]B．(0，2)C．(1，2]D．(0，＋∞)
【答案】A
【解析】∵由，即，解得，所以集合，
由当时，，得，所以．故选：A.
【例1-2】 (2023·河北保定·高三期末）设集合均为非空集合.（ ）
A．若，则 B．若，则
C．若，则 D．若，则
【答案】C
【解析】对于A,，，当时，结论不成立，则A错误；
对于B, ，当时，结论不成立，，则B错误；
对于C,因为，，所以，又，所以，则,则C正确;
对于D， ，当时，结论不成立,则D错误;故选:C.
【例1-3】 (2023·全国·高三专题练习）已知集合，，则的元素个数为（ ）
A．2B．1C．0D．无法确定
【答案】A
【解析】时，与圆相交有两个交点
时，∴直线与圆相交，有两个交点故选：A
【一隅三反】
1． (2023·浙江绍兴·高三期末）已知全集，集合，，则（ ）
A．B．C．D．
【答案】D
【解析】由，可得，即，则
由，可得或，则或
则，故故选：D
2． (2023·全国·模拟预测）已知全集，集合，，则图中阴影部分表示的集合为（ ）
A．B．C．D．
【答案】B
【解析】由，得，则，所以.\
由，得，则，则图中阴影部分表示的集合为.故选:B.
3． (2023·全国·高三专题练习）设集合，，，，则（ ）
A．B．C．D．
【答案】B
【解析】，，，，
对于集合，当时，，；
当时，，．，故选：B．
4． (2023·全国·高三专题练习）已知集合，，则中元素的个数为（ ）
A．3B．2C．1D．0
【答案】B
【解析】集合中的元素为点集，由题意，可知集合A表示以为圆心，为半径的单位圆上所有点组成的集合，集合B表示直线上所有的点组成的集合，又圆与直线相交于两点，，则中有2个元素.故选B.
考点二 集合中的参数问题
【例2-1】 (2023·全国·高三专题练习）集合或，若，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】，
①当时，即无解，此时，满足题意．
②当时，即有解，当时，可得，要使，则需要，解得．
当时，可得，要使，则需要，解得，综上，实数的取值范围是．
故选：A．
【例2-2】 (2023·全国·高三专题练习）已知集合，.若，则实数（ ）
A．3B．C．3或D．或1
【答案】A
【解析】因为，所以直线与直线没有交点，
所以直线与直线互相平行，
所以，解得或，
当时，两直线为：，，此时两直线重合，不满足，
当时，两直线为：，，此时两直线平行，满足，
所以的值为，故选：A.
【例2-3】 (2023·全国·高三专题练习（理））设集合，集合若中恰含有一个整数 ，则实数的取值范围是（ ）
A．B．C．D．
【答案】A
【解析】A={x|x＜﹣3或x＞1}， 函数y=f（x）=x2﹣2ax﹣1的对称轴为x=a＞0，
而f（﹣3）=6a+8>0，f（﹣1）=2a>0，f（0）<0，故其中较小的零点为（-1，0）之间，另一个零点大于1，f（1）<0，要使A∩B恰有一个整数，即这个整数解为2，∴f（2）≤0且f（3）＞0，
即，解得： ，即≤a＜，则a的取值范围为．故答案为：A.
【一隅三反】
1． (2023·全国·高三专题练习（理））设集合，，若，则的取值范围为（ ）
A．B．C．D．
【答案】A
【解析】，，由得，所以.故选：A.
2． (2023·全国·高三专题练习）已知集合，，若，则实数的取值集合为（ ）
A．B．C．D．
【答案】D
【解析】，因为，所以，
当时，集合，满足；
当时，集合，
由，得或，解得或，
综上，实数的取值集合为.故选：D.
3． (2023·全国·高三专题练习）已知集合，.若，则实数（ ）
A．-3B．C．D．3
【答案】B
【解析】因为，所以直线与直线平行，
所以所以. 经检验，当时，两直线平行.故选：B.
4． (2023·全国·高三专题练习（理））已知A={-1，2}，B={x|mx+1=0}，若A∪B=A，则实数m的取值所成的集合是（ ）
A．B．
C．D．
【答案】D
【解析】∵A∪B=A,∴B⊆A,∴B=∅,{−1}或{2}.m=0时，B=∅，满足条件．m≠0时，−m+1=0，或2m+1=0，
解得m=1或−.综上可得：实数m的取值所成的集合是.本题选择D选项.
考点三 集合中的新定义
【例3】 (2023·全国·高三专题练习）（多选）对任意A，，记，则称为集合A，B的对称差．例如，若，，则，下列命题中，为真命题的是（ ）
A．若A，且，则
B．若A，且，则
C．若A，且，则
D．存在A，，使得
【答案】ABD
【解析】对于A选项，因为，所以，所以，且B中的元素不能出现在中，因此，即选项A正确；
对于B选项，因为，所以，即与是相同的，所以，即选项B正确；
对于C选项，因为，所以，所以，即选项C错误；
对于D选项，时，，，D正确；故选：ABD．
【一隅三反】
1． (2023·贵州）定义集合 且.己知集合，，，则中元素的个数为（ ）
A．3B．4C．5D．6
【答案】B
【解析】因为，，所以，
又因为，所以.故选：B.
2． (2023·湖南·雅礼中学一模）已知集合，，定义集合，则中元素的个数为
A．77B．49C．45D．30
【答案】C
【解析】因为集合，所以集合中有5个元素（即5个点），即图中圆中的整点，集合中有25个元素（即25个点）：即图中正方形中的整点，集合的元素可看作正方形中的整点（除去四个顶点），即个．
3． (2023·全国·高三专题练习）若一个集合是另一个集合的子集，则称两个集合构成“鲸吞”；若两个集合有公共元素，且互不为对方子集，则称两个集合构成“蚕食”，对于集合，，若这两个集合构成“鲸吞”或“蚕食”，则a的取值集合为_____.
【答案】
【解析】当时，，此时满足，
当时，，此时集合只能是“蚕食”关系，
所以当集合有公共元素时，解得，
当集合有公共元素时，解得，
故的取值集合为.
故答案为：
4． (2023·全国·高三专题练习）若，则，就称是伙伴关系集合，集合的所有非空子集中，具有伙伴关系的集合个数为_________________.
【答案】
【解析】因为，；，；，；，；
这样所求集合即由，，“和” ，“和”这“四大”元素所组成的集合的非空子集．
所以满足条件的集合的个数为，故答案为：.
考点四 集合与其他知识的综合运用
【例4-1】 (2023·全国·高三专题练习）已知是虚数单位，集合（整数集）和的关系韦恩图如图所示，则阴影部分所示的集合的元素共有（ ）
A．3个B．2个C．1个D．无穷个
【答案】B
【解析】因为，，所以集合，
因为阴影部分所示的集合为，，
所以，阴影部分所示的集合的元素共有个，故选B．
【例4-2】 (2023·全国·模拟预测（理））已知函数的部分图象如图所示，将函数的图象向右平移个单位长度，得到函数的图象，若集合，集合，则______．
【答案】
【解析】由图可知周期，∴．
由得，∴，，
∵，∴k取0，，
∴，
∴，
∴．
∴，，
∴，∴．
故答案为：﹒
【一隅三反】
1． (2023·上海·高三专题练习）已知互异的复数满足，集合={,},则= （ ）
A．2B．1C．0D．
【答案】D
【解析】由题意或，因为，，，因此．
选D.
2． (2023·福建福州·模拟预测）从集合的非空子集中任取两个不同的集合和，若，则不同的取法共有（ ）
A．种B．种C．种D．种
【答案】C
【解析】若集合仅有个元素，则集合有种取法；集合有种取法；此时共有种取法；
若集合中有个元素，则集合有种取法；集合有种取法；此时共有种取法；
若集合中有个元素，则集合为的非空真子集，有种取法；此时共有种取法；
综上所述：不同的取法共有种.
故选：C.
3． (2023·全国·高三专题练习）函数，则集合元素的个数有（ ）
A．个B．个C．个D．个
【答案】D
【解析】当时，，解得，
当时，若，解得，
当时，若，解得，
当时，若，则，解得或.
又∵
∴或
∴或或或或.
∴集合元素的个数有5个.
故选：D．