

2024年中考数学几何模型专项复习讲与练 模型15 全等三角形——雨伞模型-原卷版+解析
展开【条件】AP是∠BAC的平分线,BO⊥AP
【结论】①△ABO≌△ADO,②AB=AD,③OB=OD
角平分线+垂直=延长
【证明】延长BO交AC于D,
在△BAO和△DAO中
∠BAO=∠DAO
AO=AO
∠AOB=∠AOD
∴△BAO≌△DAO
∴AB=AD,OB=OD
eq \\ac(○,巧) eq \\ac(○,记) eq \\ac(○,口) eq \\ac(○,诀)
角平分线+垂线,轻轻延长等腰现
1. (2023·江苏泰州·九年级专题练习)如图,ABC中,AC=BC,∠ACB=90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.
(1)线段BE与线段AD有何数量关系?并说明理由;
(2)判断BEG的形状,并说明理由.
2. (2023·全国·九年级专题练习)如图1,在平面直角坐标系中,直线分别交x轴、y轴于两点,且满足,且是常数,直线平分,交x轴于点D.
(1)若的中点为M,连接交于点N,求证:;
(2)如图2,过点A作,垂足为E,猜想与间的数量关系,并证明你的猜想.
1. (2023·广东·丰顺县小胜中学九年级开学考试)如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE
(1)求证:四边形BDEF是平行四边形
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论
2. (2023·江苏·八年级专题练习)已知,如图中,,,的平分线交于点,,
求证:.
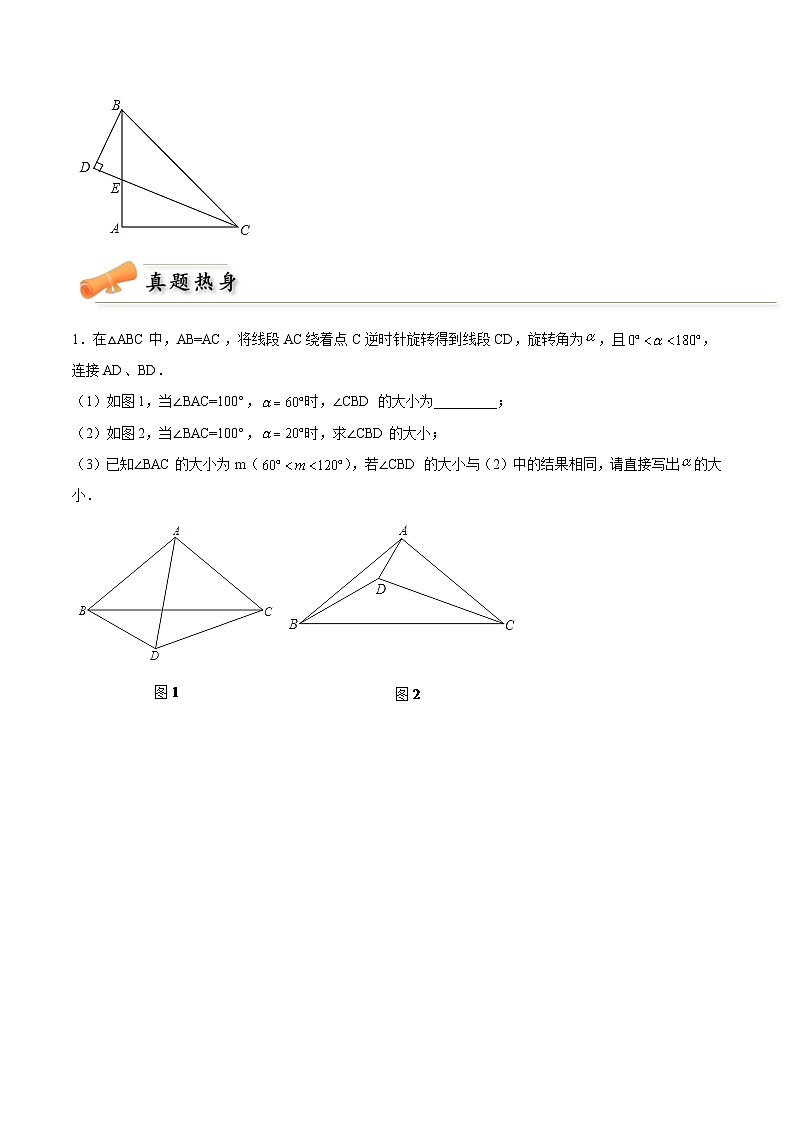
1.在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为,且,连接AD、BD.
(1)如图1,当∠BAC=100°,时,∠CBD 的大小为_________;
(2)如图2,当∠BAC=100°,时,求∠CBD的大小;
(3)已知∠BAC的大小为m(),若∠CBD 的大小与(2)中的结果相同,请直接写出的大小.
全等三角形
模型(十五)——雨伞模型
【条件】AP是∠BAC的平分线,BO⊥AP
【结论】①△ABO≌△ADO,②AB=AD,③OB=OD
角平分线+垂直=延长
【证明】延长BO交AC于D,
在△BAO和△DAO中
∠BAO=∠DAO
AO=AO
∠AOB=∠AOD
∴△BAO≌△DAO
∴AB=AD,OB=OD
eq \\ac(○,巧) eq \\ac(○,记) eq \\ac(○,口) eq \\ac(○,诀)
角平分线+垂线,轻轻延长等腰现
1. (2023·江苏泰州·九年级专题练习)如图,ABC中,AC=BC,∠ACB=90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.
(1)线段BE与线段AD有何数量关系?并说明理由;
(2)判断BEG的形状,并说明理由.
【答案】(1)BE=AD,见解析;(2)BEG是等腰直角三角形,见解析
【分析】(1)延长BE、AC交于点H,先证明△BAE≌△HAE,得BE=HE=BH,再证明△BCH≌△ACD,得BH=AD,则BE=AD;
(2)先证明CF垂直平分AB,则AG=BG,再证明∠CAB=∠CBA=45°,则∠GAB=∠GBA=22.5°,于是∠EGB=∠GAB+∠GBA=45°,可证明△BEG是等腰直角三角形.
【详解】证:(1)BE=AD,理由如下:
如图,延长BE、AC交于点H,
∵BE⊥AD,
∴∠AEB=∠AEH=90°,
∵AD平分∠BAC,
∴∠BAE=∠HAE,
在△BAE和△HAE中,
,
∴△BAE≌△HAE(ASA),
∴BE=HE=BH,
∵∠ACB=90°,
∴∠BCH=180°﹣∠ACB=90°=∠ACD,
∴∠CBH=90°﹣∠H=∠CAD,
在△BCH和△ACD中,
,
∴△BCH≌△ACD(ASA),
∴BH=AD,
∴BE=AD.
(2)△BEG是等腰直角三角形,理由如下:
∵AC=BC,AF=BF,
∴CF⊥AB,
∴AG=BG,
∴∠GAB=∠GBA,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴∠GAB=∠CAB=22.5°,
∴∠GAB=∠GBA=22.5°,
∴∠EGB=∠GAB+∠GBA=45°,
∵∠BEG=90°,
∴∠EBG=∠EGB=45°,
∴EG=EB,
∴△BEG是等腰直角三角形.
【点睛】本题考查等腰直角三角形的判定与性质,全等三角形的判定与性质等,理解等腰直角三角形的基本性质,并且掌握全等三角形中常见辅助线的作法是解题关键.
2. (2023·全国·九年级专题练习)如图1,在平面直角坐标系中,直线分别交x轴、y轴于两点,且满足,且是常数,直线平分,交x轴于点D.
(1)若的中点为M,连接交于点N,求证:;
(2)如图2,过点A作,垂足为E,猜想与间的数量关系,并证明你的猜想.
【答案】(1)见解析;(2),证明见解析.
【分析】(1)由已知条件可得,进而得,由直线平分及直角三角形斜边上中线的性质得,再由三角形的外角定理,分别求得,根据角度的等量代换,即可得,最后由等角对等边的性质即可得证;
(2)如图,延长交轴于点,先证明,得,再证明,即可得.
【详解】(1),
,
,
,
直线平分,
,
为的中点,
,
,
,
,
,
,
,
.
(2),
证明:如图,延长交轴于点,
直线平分,,
,,
又,
(ASA),
,
,
,
即,
,
又,
(ASA),
,
即.
【点睛】本题考查了平面直角坐标系的定义,非负数之和为零,三角形角平分线的定义,三角形中线的性质,三角形外角定理,三角形全等的性质与判定,等角对等边,熟练掌握以上知识,添加辅助线是解题的关键.
1. (2023·广东·丰顺县小胜中学九年级开学考试)如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE点F在AB上,且BF=DE
(1)求证:四边形BDEF是平行四边形
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论
【答案】(1)见解析;(2),理由见解析
【分析】(1)延长CE交AB于点G,证明,得E为中点,通过中位线证明DEAB,结合BF=DE,证明BDEF是平行四边形
(2)通过BDEF为平行四边形,证得BF=DE=BG,再根据,得AC=AG,用AB-AG=BG,可证
【详解】(1)证明:延长CE交AB于点G
∵AECE
∴
在和
∴
∴GE=EC
∵BD=CD
∴DE为的中位线
∴DEAB
∵DE=BF
∴四边形BDEF是平行四边形
(2)
理由如下:
∵四边形BDEF是平行四边形
∴BF=DE
∵D,E分别是BC,GC的中点
∴BF=DE=BG
∵
∴AG=AC
BF=(AB-AG)=(AB-AC).
【点睛】本题主要考查了平行四边形的证明,中位线的性质,全等三角形的证明等综合性内容,作好适当的辅助线,是解题的关键.
2. (2023·江苏·八年级专题练习)已知,如图中,,,的平分线交于点,,
求证:.
【答案】见解析.
【分析】延长BD交CA的延长线于F,先证得△ACE≌△ABF,得出CE=BF;再证△CBD≌△CFD,得出BD=DF;由此得出结论即可.
【详解】证明:如图,
延长交的延长线于,
平分
【点睛】此题考查三角形全等的判定与性质,角平分线的性质,根据已知条件,作出辅助线是解决问题的关键.
1.在△ABC中,AB=AC,将线段AC绕着点C逆时针旋转得到线段CD,旋转角为,且,连接AD、BD.
(1)如图1,当∠BAC=100°,时,∠CBD 的大小为_________;
(2)如图2,当∠BAC=100°,时,求∠CBD的大小;
(3)已知∠BAC的大小为m(),若∠CBD 的大小与(2)中的结果相同,请直接写出的大小.
【答案】(1)30°;(2)30°;(3)为或或.
【分析】(1)由,,可以确定,旋转角为,时是等边三角形,且,知道的度数,进而求得的大小;
(2)由,,可以确定,连接、.,,,由案.依次证明,.利用角度相等可以得到答案.
(3)结合(1)(2)的解题过程可以发现规律,是等边三角形时,在内部时,在外部时,求得答案.
【详解】解:(1)解(1)∵,,
∴,
∵,,
∴为等边三角形,
∴.
又∵,
∴为等腰三角形,
∴,
∴.
(2)方法1:如图作等边,连接、.
,.
,,
.
,
.
.①
,,
.②
,③
由①②③,得,
,.
,,
.
,,
.
.
.④
,,
.⑤
,⑥
由④⑤⑥,得.
.
.
.
.
方法2 如下图所示,构造等边三角形ADE,连接CE.
∵在等腰三角形ACD中,,
∴,
∵,
∴.
可证.
结合角度,可得,.
在和中,
,
∴,
∴.
∵,
∴.
方法3 如下图所示,平移CD至AE,连接ED,EB,则四边形ACDE是平行四边形.
∵,
∴四边形ACDE是菱形,
∴,.
∴,
∴,
∴是等边三角形,是等腰三角形,
∴,,
∴.
∴.
(3)由(1)知道,若,时,则;
①由(1)可知,设时可得,,
,
.
②由(2)可知,翻折到△,则此时,
,
,
③以为圆心为半径画圆弧交的延长线于点,连接,
,
.
综上所述,为或或时,.
【点睛】本题是一道几何结论探究题,解答这类题目的关键是要善于从探究特殊结论中归纳出一般性解题方法,并灵活运用这种方法解答一般性的问题,真正达到举一反三的目的.
2024年中考数学几何模型专项复习讲与练 模型16 全等三角形——半角模型-原卷版+解析: 这是一份2024年中考数学几何模型专项复习讲与练 模型16 全等三角形——半角模型-原卷版+解析,共28页。
中考数学几何模型专项复习 模型33 旋转——奔驰模型-(原卷版+解析): 这是一份中考数学几何模型专项复习 模型33 旋转——奔驰模型-(原卷版+解析),共20页。
中考数学几何模型专项复习 模型17 全等三角形——胖瘦模型(SSA)-(原卷版+解析): 这是一份中考数学几何模型专项复习 模型17 全等三角形——胖瘦模型(SSA)-(原卷版+解析),共22页。












