2024年中考数学几何模型专项复习讲与练 模型30 平行四边形——十字架模型-原卷版+解析

这是一份2024年中考数学几何模型专项复习讲与练 模型30 平行四边形——十字架模型-原卷版+解析，共21页。

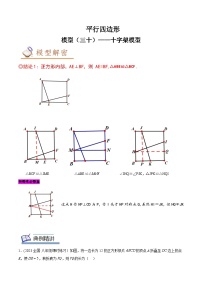
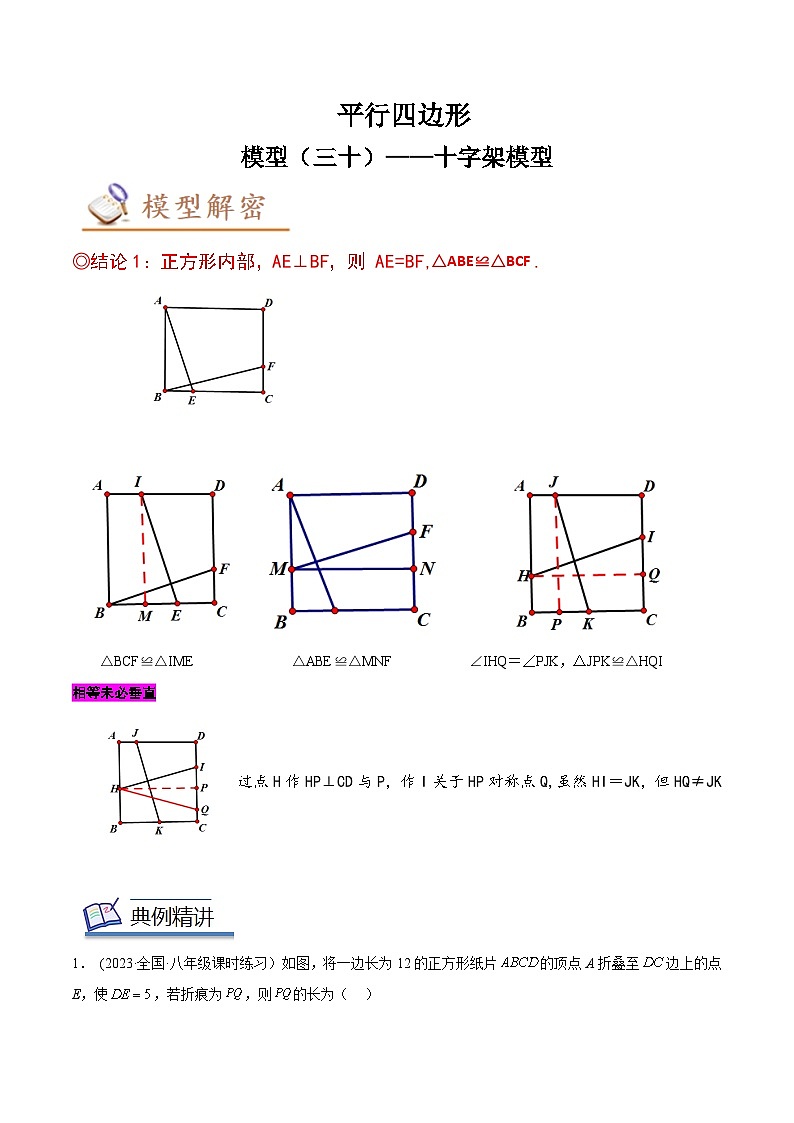
◎结论1：正方形内部，AE⊥BF，则 AE=BF,△ABE≌△BCF .



△BCF≌△IME △ABE≌△MNF ∠IHQ＝∠PJK，△JPK≌△HQI
相等未必垂直
过点H作HP⊥CD与P，作I关于HP对称点Q,虽然HI＝JK，但HQ≠JK
1． (2023·全国·八年级课时练习）如图，将一边长为12的正方形纸片的顶点A折叠至边上的点E，使，若折痕为，则的长为（ ）
A．13B．14C．15D．16
2． (2023·黑龙江牡丹江·中考真题）如图，正方形ABCD的边长为3，E为BC边上一点，BE＝1.将正方形沿GF折叠，使点A恰好与点E重合，连接AF，EF，GE，则四边形AGEF的面积为（ ）
A．2B．2C．6D．5
3． (2023·广东·模拟预测）如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长为（ ）
A．B．3C．D．
1． (2023·全国·八年级专题练习）如图，在正方形ABCD中，点E是BC上一点，BF⊥AE交DC于点F，若AB＝5，BE＝2，则AF＝____．
2． (2023·江苏盐城·八年级期中）如图，将一边长为的正方形纸片的顶点折叠至边上的点，使，折痕为，则的长__________．
3． (2023·江苏泰州·八年级期末）如图，正方形ABCD边长为4，点G在边AD上（不与点A、D重合），BG的垂直平分线分别交AB、CD于E、F两点，连接EG．
（1）当AG=1时，求EG的长；
（2）当AG的值等于 时，BE=8－2DF；
（3）过G点作GM⊥EG交CD于M
①求证：GB平分∠AGM；
②设AG=x，CM=y，试说明的值为定值．
1． (2023·云南曲靖·八年级期末）如图1，在正方形中，为上一点，连接，过点作于点，交于点．
（1）求证：；
（2）如图2，连接、，点、、、分别是、、、的中点，试判断四边形的形状，并说明理由；
（3）如图3，点、分别在正方形的边、上，把正方形沿直线翻折，使得的对应边恰好经过点，过点作于点，若，正方形的边长为3，求线段的长．
2．正方形ABCD中，点E、F在BC、CD上，且BE＝CF，AE与BF交于点G．
（1）如图1，求证AE⊥BF；
（2）如图2，在GF上截取GM＝GB，∠MAD的平分线交CD于点H，交BF于点N，连接CN，求证：AN+CN＝BN；

平行四边形
模型（三十）——十字架模型


◎结论1：正方形内部，AE⊥BF，则 AE=BF,△ABE≌△BCF .



△BCF≌△IME △ABE≌△MNF ∠IHQ＝∠PJK，△JPK≌△HQI
相等未必垂直
过点H作HP⊥CD与P，作I关于HP对称点Q,虽然HI＝JK，但HQ≠JK
1． (2023·全国·八年级课时练习）如图，将一边长为12的正方形纸片的顶点A折叠至边上的点E，使，若折痕为，则的长为（ ）
A．13B．14C．15D．16
【答案】A
【分析】过点P作PM⊥BC于点M，由折叠得到PQ⊥AE，从而得到∠AED=∠APQ，可得△PQM≌△ADE，从而得到PQ=AE，再由勾股定理，即可求解．
【详解】解：过点P作PM⊥BC于点M，
由折叠得到PQ⊥AE，
∴∠DAE+∠APQ=90°，
在正方形ABCD中，AD∥BC，∠D=90°，CD⊥BC，
∴∠DAE+∠AED=90°，
∴∠AED=∠APQ，
∴∠APQ=∠PQM，
∴∠PQM=∠APQ=∠AED，
∵PM⊥BC，
∴PM=AD，
∵∠D=∠PMQ=90°，
∴△PQM≌△ADE，
∴PQ=AE，
在 中，，AD=12，
由勾股定理得：
，
∴PQ=13．
故选：A．
【点睛】本题主要考查了正方形的性质，全等三角形的判定和性质，勾股定理，得到△PQM≌△ADE是解题的关键．
2． (2023·黑龙江牡丹江·中考真题）如图，正方形ABCD的边长为3，E为BC边上一点，BE＝1.将正方形沿GF折叠，使点A恰好与点E重合，连接AF，EF，GE，则四边形AGEF的面积为（ ）
A．2B．2C．6D．5
【答案】D
【分析】作FH⊥AB于H，交AE于P，设AG=GE=x，在Rt△BGE中求出x，在Rt△ABE中求出AE，再证明△ABE≌△FHG，得到FG=AE，然后根据S四边形AGEF=S△AGF+S△EGF求解即可
【详解】解：作FH⊥AB于H，交AE于P，则四边形ADFH是矩形，由折叠的性质可知，AG=GE，AE⊥GF，AO=EO．
设AG=GE=x，则BG=3-x，
在Rt△BGE中，
∵BE2+BG2=GE2，
∴12+(3-x)2=x2，
∴x=．
在Rt△ABE中，
∵AB2+BE2=AE2，
∴32+12=AE2，
∴AE=．
∵∠HAP+∠APH=90°，∠OFP+∠OPF=90°，∠APH=∠OPF，
∴∠HAP=∠OFP，
∵四边形ADFH是矩形，
∴AB=AD=HF．
在△ABE和△FHG中，
，
∴△ABE≌△FHG，
∴FG=AE=，
∴S四边形AGEF=S△AGF+S△EGF
=
=
=
=
=5．
故选D．
【点睛】本题考查了折叠的性质，正方形的性质，矩形的判定与性质，三角形的面积，以及勾股定理等知识，熟练掌握折叠的性质是解答本题的关键．
3． (2023·广东·模拟预测）如图，将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q处，折痕为FH，则线段AF的长为（ ）
A．B．3C．D．
【答案】C
【分析】设EF=FD=x，在RT△AEF中利用勾股定理即可解决问题．
【详解】解：∵将边长为6cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，
∴EF＝DE，AB＝AD＝6cm，∠A＝90°
∵点E是AB的中点，
∴AE＝BE＝3cm，
在Rt△AEF中，EF2＝AF2+AE2，
∴（6﹣AF）2＝AF2+9
∴AF＝
故选C．
【点睛】本题考查翻折变换、正方形的性质、勾股定理等知识，解题的关键是设未知数利用勾股定理列出方程解决问题，属于中考常考题型．
1． (2023·全国·八年级专题练习）如图，在正方形ABCD中，点E是BC上一点，BF⊥AE交DC于点F，若AB＝5，BE＝2，则AF＝____．
【答案】.
【分析】根据正方形的性质得到AB＝BC，∠ABE＝∠BCF＝90°，推出∠BAE＝∠EBH，根据全等三角形的性质得到CF＝BE＝2，求得DF＝5﹣2＝3，根据勾股定理即可得到结论．
【详解】∵四边形ABCD是正方形，
∴AB＝BC，∠ABE＝∠BCF＝90°，
∴∠BAE+∠AEB＝90°，
∵BH⊥AE，
∴∠BHE＝90°，
∴∠AEB+∠EBH＝90°，
∴∠BAE＝∠EBH，
在△ABE和△BCF中，
∴△ABE≌△BCF（ASA），
∴CF＝BE＝2，
∴DF＝5﹣2＝3，
∵四边形ABCD是正方形，
∴AB＝AD＝5，∠ADF＝90°，
由勾股定理得：AF＝＝＝．
故答案为．
【点睛】此题考查了正方形的性质、全等三角形的判定与性质、勾股定理，本题证明△ABE≌△BCF是解本题的关键．
2． (2023·江苏盐城·八年级期中）如图，将一边长为的正方形纸片的顶点折叠至边上的点，使，折痕为，则的长__________．
【答案】13
【分析】先过点P作PM⊥BC于点M，利用三角形全等的判定得到△PQM≌△AED，从而求出PQ=AE．
【详解】过点P作PM⊥BC于点M，
由折叠得到PQ⊥AE，
∴∠DAE+∠APQ=90°，
又∠DAE+∠AED=90°，
∴∠AED=∠APQ，
∵AD∥BC，
∴∠APQ=∠PQM，
则∠PQM=∠APQ=∠AED，∠D=∠PMQ，PM=AD
∴△PQM≌△AED
∴PQ=AE==13．
故答案是：13．
【点睛】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．
3． (2023·江苏泰州·八年级期末）如图，正方形ABCD边长为4，点G在边AD上（不与点A、D重合），BG的垂直平分线分别交AB、CD于E、F两点，连接EG．
（1）当AG=1时，求EG的长；
（2）当AG的值等于 时，BE=8－2DF；
（3）过G点作GM⊥EG交CD于M
①求证：GB平分∠AGM；
②设AG=x，CM=y，试说明的值为定值．
【答案】（1）；（2）（3）①见解析；②，理由见解析
【分析】（1）根据EF是线段BG的垂直平分线，BE=EG，设EG=EB=x，则AE=AB-BE=4-x，再由勾股定理求解即可；
（2）过点F作FH⊥AB于H，连接FB，FG，由BE=8-2DF，CF=CD-DF=4-DF，得到BE=2CF，先证明四边形BCFH是矩形，得到CF=HB，则BH=EH=FC，设AG=x，BE=y，则AE=4-y，GD=4-x，CF=，由，，，可以得到①，②，联立①②求解即可得到答案；
（3）①先证明∠EBG=∠EGB，然后根据ABG+∠AGB=90°，∠EGB+∠BGM=90°，即可得到∠AGB=∠BGM；
②连接BM，过点B作BH⊥GM，由角平分线的性质得到BH=AB=4，由，可以得到，由勾股定理可以得到即，最后解方程即可得到答案．
【详解】解：（1）∵EF是线段BG的垂直平分线，
∴BE=EG，
∵四边形ABCD是正方形，且边长为4，
∴AB=4，∠A=90°，
设EG=EB=x，则AE=AB-BE=4-x，
∵，
∴，
解得，
∴；
（2）如图所示，过点F作FH⊥AB于H，连接FB，FG
∵EF是线段BG的垂直平分线，
∴BF=FG，
∵BE=8-2DF，CF=CD-DF=4-DF，
∴BE=2CF，
∵四边形ABCD是正方形，FH⊥AB，
∴∠HBC=∠C=∠BHF=90°，
∴四边形BCFH是矩形，
∴CF=HB，
∴BH=EH=FC，
设AG=x，BE=y，则AE=4-y，GD=4-x，CF=，
∵，，，
∴①，②，
联立①②解得或（舍去），
∴当时，BE=8-2DF，
故答案为：；
（3）①∵EF是线段BG的垂直平分线，
∴EG=BE，
∴∠EBG=∠EGB，
∵四边形ABCD是正方形，EG⊥GM，
∴∠A=∠EGM=90°，
∴∠ABG+∠AGB=90°，∠EGB+∠BGM=90°，
∴∠AGB=∠BGM，
∴BG平分∠AGM；
②如图，连接BM，过点B作BH⊥GM，
由（3）①得BG平分∠AGM，
∴BH=AB=4，
∵AG=x，CM=y，
∴DG=4-x，DM=4-y，
∵，
∴，
∴，
∴，
∵，
∴
∴
∴，
∴，
∴，
当时，则，
∴（不符合题意），
∴
∴．
【点睛】本题主要考查了正方形的性质，勾股定理，角平分线的性质，线段垂直平分线的性质，等腰三角形的性质与判定，三角形的面积等等，解题的关键在于能够熟练掌握相关知识进行求解．
1． (2023·云南曲靖·八年级期末）如图1，在正方形中，为上一点，连接，过点作于点，交于点．
（1）求证：；
（2）如图2，连接、，点、、、分别是、、、的中点，试判断四边形的形状，并说明理由；
（3）如图3，点、分别在正方形的边、上，把正方形沿直线翻折，使得的对应边恰好经过点，过点作于点，若，正方形的边长为3，求线段的长．
【答案】（1）见解析；（2）四边形为正方形，理由见解析；（3）
【分析】（1）由四边形为正方形，可得，推得，由，可得，可证即可；
（2）、为、中点，可得为的中位线，可证，，由点、、、分别是、、、的中点，可得PQ是的中位线，MQ为的中位线，NP为的中位线，可证，，，，，，可证四边形为平行四边形．再证四边形为菱形，最后证即可；
（3）延长交于点，由对称性可得，，，由勾股定理可求，可得，设，在中，，解得，在中，可求．
【详解】（1）证明：∵四边形为正方形，
∴，
∴，
∵，
∴∠AHB=90°，
∴，
∴，
在与中，
，
∴，
∴．
（2）解：四边形为正方形，理由如下：
∵、为、中点，
∴为的中位线，
∴，，
∵点、、、分别是、、、的中点，
∴PQ是的中位线，MQ为的中位线，NP为的中位线，，
∴，，，，，，
∴，，
∴四边形为平行四边形．
∵，
∴，
∴四边形为菱形，
∵，，
∴，
∵，
∴，
∴四边形为正方形．
（3）解：延长交于点，
由对称性可知
，，，
在中，
，
∴，
设，则，
在中，
，
，
∴，
在中，
．
【点睛】本题考查正方形性质与判定，等角的余角性质三角形全等判定与性质，三角形中位线判定与性质，勾股定理，根据勾股定理建构方程，解拓展一元一次方程等知识，掌握以上知识是解题关键．
2．正方形ABCD中，点E、F在BC、CD上，且BE＝CF，AE与BF交于点G．
（1）如图1，求证AE⊥BF；
（2）如图2，在GF上截取GM＝GB，∠MAD的平分线交CD于点H，交BF于点N，连接CN，求证：AN+CN＝BN；
【答案】（1）见解析；（2）见解析；
【分析】（1）根据正方形的性质得AB=BC，，用SAS证明，得，根据三角形内角和定理和等量代换即可得；
（2）过点B作，交AN于点H，根据正方形的性质和平行线的性质，用SAS证明，得，根据角平分线性质得，则是等腰直角三角形，用SAS证明，得AH=CN，在中，根据勾股定理即可得；
【详解】解：（1）∵四边形ABCD 是正方形，
∴AB=BC，，
在和中，
∴（SAS），
∴，
∵，
∴，
∴，
∴；
（2）如图所示，过点B作，交AN于点H，
∵四边形ABCD是正方形，
∴AB=AC，，
∵，
，
∴，
由（1）得，，
∴，
∴,
∴，
∴，
在和中，
∴（SAS），
∴，
∵AN平分，
∴，
∴，
，
，
，
∴，
∴，
∴是等腰直角三角形，
∴BH=BN，
在和中，
∴（SAS），
∴AH=CN，
在中，根据勾股定理
，
∴；
【点睛】本题考查了正方形的性质，全等三角形的判定与性质，三角形内角和定理，角平分线，等腰直角三角形的判定与性质，勾股定理和锐角三角函数，解题的关键是掌握并灵活运用这些知识点．