

所属成套资源:2024年中考数学几何模型专项复习讲与练(原卷版+解析)
2024年中考数学几何模型专项复习讲与练 模型36 圆——四点共圆模型-原卷版+解析
展开
这是一份2024年中考数学几何模型专项复习讲与练 模型36 圆——四点共圆模型-原卷版+解析,共18页。
四点共圆:如果同一平面内的四个点在同一圆上,则称这四个点共圆
知识点一:四点共圆的性质
◎结论1:如图 A、B、C、D四点共圆
①同侧共底的两个三角形顶角相等(同弧所对的圆周角相等)
∠ACB=∠ADB,AB为底;∠BAC=∠BDC,BC为底;
∠CAD=∠CBD,CD为底;∠ABD=∠ACD,AD为底;
②圆内接四边形的对角互补
∠ABC+∠ADC=180º;∠BCD+∠BAD=180
③圆内接四边形的外角等于内对角
∠BCE为圆内接四边形的一个外角,
则∠BCE=∠A
知识点二:四点共圆的判定
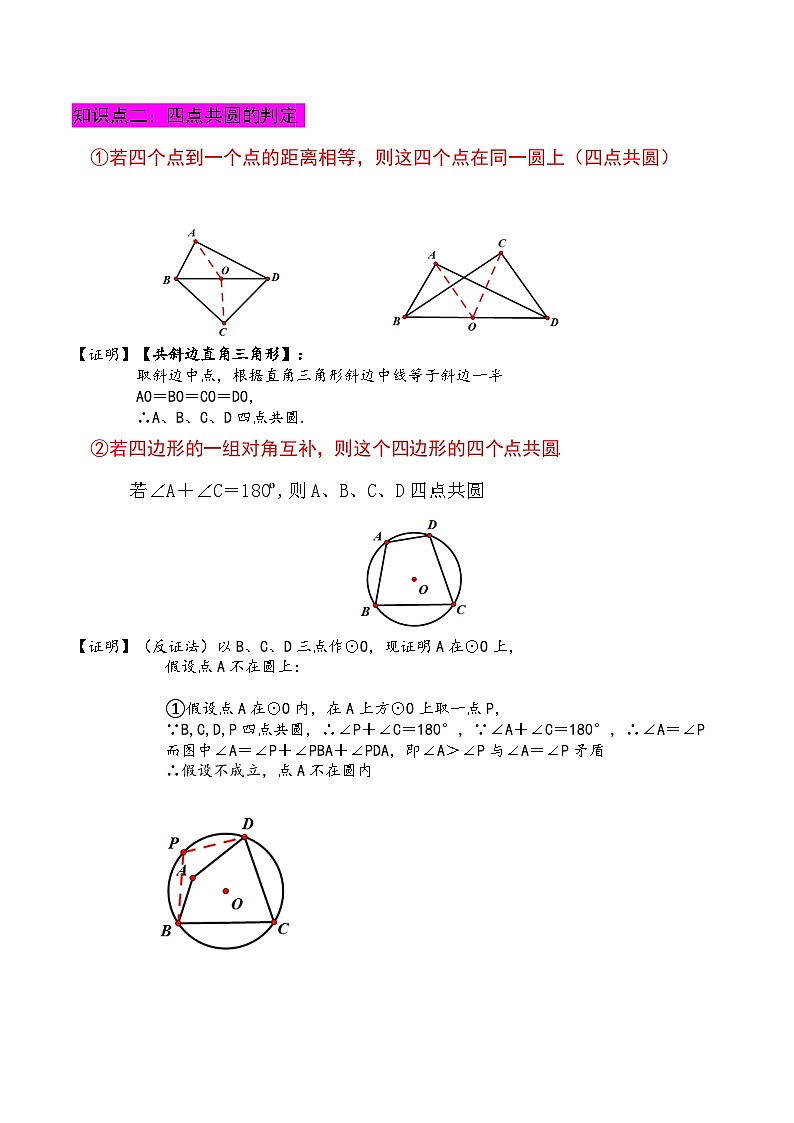
①若四个点到一个点的距离相等,则这四个点在同一圆上(四点共圆)
【证明】【共斜边直角三角形】:
取斜边中点,根据直角三角形斜边中线等于斜边一半
AO=BO=CO=DO,
∴A、B、C、D四点共圆.
②若四边形的一组对角互补,则这个四边形的四个点共圆.
若∠A+∠C=180º,则A、B、C、D四点共圆
【证明】(反证法)以B、C、D三点作⊙O,现证明A在⊙O上,
假设点A不在圆上:
①假设点A在⊙O内,在A上方⊙O上取一点P,
∵B,C,D,P四点共圆,∴∠P+∠C=180°,∵∠A+∠C=180°,∴∠A=∠P
而图中∠A=∠P+∠PBA+∠PDA,即∠A>∠P与∠A=∠P矛盾
∴假设不成立,点A不在圆内
②假设点A在⊙O外,在A上方⊙O上取一点P,
∵B,C,D,P四点共圆,∴∠P+∠C=180°,∵∠A+∠C=180°,∴∠A=∠P
而图中∠A=∠P+∠PBA+∠PDA,即∠A>∠P与∠A=∠P矛盾
∴假设不成立,点A不在圆外。
综上:A只能在圆上,即A,B,C,D四点共圆。
③若一个四边形的外角等于它的内对角,则这个四边形四点共圆
若∠BCD=∠A,则A、B、C、D四点共圆
【本质:对角互补】
④若两个点在一条线段的同旁,且和这条线段的两个端点连线所夹的角相等,那么这两个点和这条线段的两个端点四点共圆
若∠BAC=∠BDC,则A、B、C、D四点共圆
证明:以A.B.C作圆,在弧BC上取点P,
则∠BAC+∠P=180°,
∵∠BAC=∠BDC,
∴∠P+∠BDC=180°,
∴四点共圆
∵四点共圆,
B.P.C确定唯一圆
∴四点共圆.
1. (2023·全国·九年级专题练习)如图,已知AB=AC=AD,∠CAD=20°,则∠CBD的度数是( )
A.10°B.15°C.20°D.25°
2. (2023·全国·九年级专题练习)如图,在长方形中,,,垂足为,延长交于,表示面积,则给出的下列命题:①;②;③;④.其中正确命题的代号是________.
3. (2023·黑龙江哈尔滨·九年级阶段练习)如图,等边△ABC中,D在BC上,E在AC上,BD=CE,连BE、AD交于F,T在EF上,且DT=CE,AF=50,TE=16,则FT=_____.
1. (2023·全国·九年级课时练习)如图1,在正方形中,点在边上,过点作,且,连接、,点是的中点,连接.
(1)用等式表示线段与的数量关系:______;
(2)将图1中的绕点按逆时针旋转,使的顶点恰好在正方形的对角线上,点仍是的中点,连接、.
①在图2中,依据题意补全图形;
②用等式表示线段与的数量关系并证明.
2. (2023·福建·厦门市松柏中学九年级阶段练习)如图,等腰三角形△ABC中,∠BAC=120°,AB=3.
(1)求BC的长.
(2)如图,点D在CA的延长线上,DE⊥AB于E,DF⊥BC于F,连EF.求EF的最小值.
1. (2023·福建·中考真题)如图,四边形内接于,,为中点,,则等于( )
A.B.C.D.
圆
模型(三十六)——四点共圆模型
四点共圆:如果同一平面内的四个点在同一圆上,则称这四个点共圆
知识点一:四点共圆的性质
◎结论1:如图 A、B、C、D四点共圆
①同侧共底的两个三角形顶角相等(同弧所对的圆周角相等)
∠ACB=∠ADB,AB为底;∠BAC=∠BDC,BC为底;
∠CAD=∠CBD,CD为底;∠ABD=∠ACD,AD为底;
②圆内接四边形的对角互补
∠ABC+∠ADC=180º;∠BCD+∠BAD=180
③圆内接四边形的外角等于内对角
∠BCE为圆内接四边形的一个外角,
则∠BCE=∠A
知识点二:四点共圆的判定
①若四个点到一个点的距离相等,则这四个点在同一圆上(四点共圆)
【证明】【共斜边直角三角形】:
取斜边中点,根据直角三角形斜边中线等于斜边一半
AO=BO=CO=DO,
∴A、B、C、D四点共圆.
②若四边形的一组对角互补,则这个四边形的四个点共圆.
若∠A+∠C=180º,则A、B、C、D四点共圆
【证明】(反证法)以B、C、D三点作⊙O,现证明A在⊙O上,
假设点A不在圆上:
①假设点A在⊙O内,在A上方⊙O上取一点P,
∵B,C,D,P四点共圆,∴∠P+∠C=180°,∵∠A+∠C=180°,∴∠A=∠P
而图中∠A=∠P+∠PBA+∠PDA,即∠A>∠P与∠A=∠P矛盾
∴假设不成立,点A不在圆内
②假设点A在⊙O外,在A上方⊙O上取一点P,
∵B,C,D,P四点共圆,∴∠P+∠C=180°,∵∠A+∠C=180°,∴∠A=∠P
而图中∠A=∠P+∠PBA+∠PDA,即∠A>∠P与∠A=∠P矛盾
∴假设不成立,点A不在圆外。
综上:A只能在圆上,即A,B,C,D四点共圆。
③若一个四边形的外角等于它的内对角,则这个四边形四点共圆
若∠BCD=∠A,则A、B、C、D四点共圆
【本质:对角互补】
④若两个点在一条线段的同旁,且和这条线段的两个端点连线所夹的角相等,那么这两个点和这条线段的两个端点四点共圆
若∠BAC=∠BDC,则A、B、C、D四点共圆
证明:以A.B.C作圆,在弧BC上取点P,
则∠BAC+∠P=180°,
∵∠BAC=∠BDC,
∴∠P+∠BDC=180°,
∴四点共圆
∵四点共圆,
B.P.C确定唯一圆
∴四点共圆.
1. (2023·全国·九年级专题练习)如图,已知AB=AC=AD,∠CAD=20°,则∠CBD的度数是( )
A.10°B.15°C.20°D.25°
【答案】A
【详解】
如图,AB=AC=AD
∵
,
故选A.
2. (2023·全国·九年级专题练习)如图,在长方形中,,,垂足为,延长交于,表示面积,则给出的下列命题:①;②;③;④.其中正确命题的代号是________.
【答案】①③④
【分析】由矩形的性质得出,,,由证明,①正确;由的面积的面积,得出的面积的面积,②不正确;证明、、、四点共圆,得出,③正确;延长交矩形的外接圆于,连接,由圆周角定理得出,由三角形的外角性质得出,得出,④正确;即可得出结论.
【详解】解:∵四边形是矩形,
∴,,,
在和中,
,
∴,
∴①正确;
∵的面积的面积,
∴的面积的面积,
∴②不正确;
∵,
∴,
∴,
∴、、、四点共圆,
∴,
∴③正确;
∵、、、四点共圆,
如图所示:
延长交矩形的外接圆于,连接,
则,
∵,
∴,
∴④正确;
正确的代号是①③④;
故答案为:①③④.
【点睛】本题考查了矩形的性质,全等三角形的判定与性质,以及圆周角的性质,掌握四点共圆的证明方法进行转化是解题关键.
3. (2023·黑龙江哈尔滨·九年级阶段练习)如图,等边△ABC中,D在BC上,E在AC上,BD=CE,连BE、AD交于F,T在EF上,且DT=CE,AF=50,TE=16,则FT=_____.
【答案】17
【分析】用“SAS”可判定△ABD≌△BCE,得到∠AFE=60°,延长FE至点G,使得FG=FA,连AG,AT,得到△AFG是等边三角形,证明A、B、D、T四点共圆,设法证明△FAT≌△GAE(ASA),即可求得答案.
【详解】∵△ABC为等边三角形,
∴AB=AC=BC,∠ABD=∠BCE=60°,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠ADC=∠CBE+∠BFD=∠BAD+∠B,
∴∠BFD=∠B=∠AFE=60°;
延长FE至点G,使得FG=FA,连AG,AT,
∵∠AFE=60°,
∴△AFG是等边三角形,
∴AG=AF=FG=50,∠AGF=∠FAG=60°,
∵∠BAF+∠EAF =∠CAG+∠EAF =60°,
∴∠BAF=∠CAG,
∵DT=CE,
∴∠DBT=∠BTD,
∵∠BAD=∠CBE,
∴∠BAD=∠BTD,
∴A、B、D、T四点共圆,
∴∠BAD=∠DAT,
∴∠FAT=∠GAE,
在△FAT和△GAE中,
,
∴△FAT≌△GAE(ASA),
∴FT= GE,
∵FG=50,TE=16,
∴FT=(FG- TE)=17.
故答案为:17.
【点睛】本题主要考查了等边三角形的判定和性质,全等三角形的判定和性质,圆周角定理等,作出辅助线,判断出△FAT≌△GAE是解本题的关键.
1. (2023·全国·九年级课时练习)如图1,在正方形中,点在边上,过点作,且,连接、,点是的中点,连接.
(1)用等式表示线段与的数量关系:______;
(2)将图1中的绕点按逆时针旋转,使的顶点恰好在正方形的对角线上,点仍是的中点,连接、.
①在图2中,依据题意补全图形;
②用等式表示线段与的数量关系并证明.
【答案】(1);(2)①画图见解析;②,证明见解析
【分析】(1)先判断出△AGB≌△CGB,得到∠GBF=45°,再判断出△EFG≌△CFG,得到∠GFB=45°,从而得到△BGF为等腰直角三角形,即可.
(2)①画图2即可;②如图2,连接BF、BG,证明△ADF≌△ABF得DF=BF,根据直角三角形斜边中线的性质得:AG=EG=BG=FG,由圆的定义可知:点A、F、E、B在以点G为圆心,AG长为半径的圆上,∠BGF=2∠BAC=90°,所以△BGF是等腰直角三角形,可得结论.
【详解】解:(1)BF=,
理由是:如图1,连接BG,CG,
∵四边形ABCD为正方形,
∴∠ABC=90°,∠ACB=45°,AB=BC,
∵EF⊥BC,FE=FC,
∴∠CFE=90°,∠ECF=45°,
∴∠ACE=90°,
∵点G是AE的中点,
∴EG=CG=AG,
∵BG=BG,
∴△AGB≌△CGB(SSS),
∴∠ABG=∠CBG=∠ABC=45°,
∵EG=CG,EF=CF,FG=FG,
∴△EFG≌△CFG(SSS),
∴∠EFG=∠CFG=(360°﹣∠BFE)=(360°﹣90°)=135°,
∵∠BFE=90°,
∴∠BFG=45°,
∴△BGF为等腰直角三角形,
∴BF=FG.
故答案为:BF=FG;
(2)①如图2所示,
②;理由如下:
如图2,连接BF、BG,
∵四边形ABCD是正方形,
∴AD=AB,∠ABC=∠BAD=90°,AC平分∠BAD,
∴∠BAC=∠DAC=45°,
∵AF=AF,
∴△ADF≌△ABF(SAS),
∴DF=BF,
∵EF⊥AC,∠ABC=90°,点G是AE的中点,
∴AG=EG=BG=FG,
∴点A、F、E、B在以点G为圆心,AG长为半径的圆上,
∵,∠BAC=45°,
∴∠BGF=2∠BAC=90°,
∴△BGF是等腰直角三角形,
∴BF=FG,
∴DF=FG.
【点睛】本题是四边形综合题,主要考查了正方形的性质,直角三角形斜边中线的性质,全等三角形的判定和性质,圆的性质,判断△BGF为等腰直角三角形是解本题的关键,作出辅助线是解本题的难点.
2. (2023·福建·厦门市松柏中学九年级阶段练习)如图,等腰三角形△ABC中,∠BAC=120°,AB=3.
(1)求BC的长.
(2)如图,点D在CA的延长线上,DE⊥AB于E,DF⊥BC于F,连EF.求EF的最小值.
【答案】(1)BC=;(2)EF的最小值为
【分析】(1)过点A作AM⊥BC于点M,根据等腰三角形的性质得∠B=30°,BM=CM,由直角三角形的性质得BM=,进而即可求解;
(2)连接BD,取BD的中点O,连接OE,OF,易得B,D,E,F四点共圆,从而得∆OEF是等边三角形,进而得EF=BD,由BD⊥CD时, BD的值最小,进而即可求解.
【详解】(1)过点A作AM⊥BC于点M,
∵等腰三角形△ABC中,∠BAC=120°,AB=3,
∴∠B=(180°-120°)÷2=30°,BM=CM,
∴BM=3÷2×=,
∴BC=2 BM=2×=3;
(2)连接BD,取BD的中点O,连接OE,OF,
∵DE⊥AB于E,DF⊥BC于F,
∴在Rt∆BDF与Rt∆BDE中,OB=OD=OE=OF=BD,
∴B,D,E,F四点共圆,
∴∠EOF=2∠EBF=2×30°=60°,
∴∆OEF是等边三角形,
∴EF=OF=BD,
∵∠C=∠EBF =30°,
∴当BD⊥CD时,BD=BC=,此时,BD的值最小,
∴EF的最小值=BD =×=.
【点睛】本题主要考查圆的基本性质以及等腰三角形,直角三角形的性质定理,添加辅助线,构造四边形的外接圆,是解题的关键.
1. (2023·福建·中考真题)如图,四边形内接于,,为中点,,则等于( )
A.B.C.D.
【答案】A
【分析】根据,为中点求出∠CBD=∠ADB=∠ABD,再根据圆内接四边形的性质得到∠ABC+∠ADC=180°,即可求出答案.
【详解】∵为中点,
∴,
∴∠ADB=∠ABD,AB=AD,
∵,
∴∠CBD=∠ADB=∠ABD,
∵四边形内接于,
∴∠ABC+∠ADC=180°,
∴3∠ADB+60°=180°,
∴=40°,
故选:A.
【点睛】此题考查圆周角定理:在同圆中等弧所对的圆周角相等、相等的弦所对的圆周角相等,圆内接四边形的性质:对角互补.
相关试卷
这是一份2024年中考数学几何模型专项复习讲与练 模型39 圆——折弦定理模型-原卷版+解析,共20页。
这是一份2024年中考数学几何模型专项复习讲与练 模型38 圆——垂径定理模型-原卷版+解析,共14页。
这是一份2024年中考数学几何模型专项复习讲与练 模型37 圆——定弦定角模型-原卷版+解析,共18页。








