2024年中考数学几何模型专项复习讲与练 模型37 圆——定弦定角模型-原卷版+解析

这是一份2024年中考数学几何模型专项复习讲与练 模型37 圆——定弦定角模型-原卷版+解析，共18页。

定弦定角：线段定，角度大小定
知识点一:
解题步骤：
寻找张角
根据张角动线段、确定隐形圆
定角是圆周角，找圆心，定半径
◎结论1：如图，AB定长，P动点，保持∠APB ＝，则点P在AB所对的圆弧上运动。

◎结论2：90°，如图AB定长，P动点，保持∠APB ＝90º，则点P在以AB为直径的圆弧上运动（不包含A、B两点）

知识点二：30º、150°
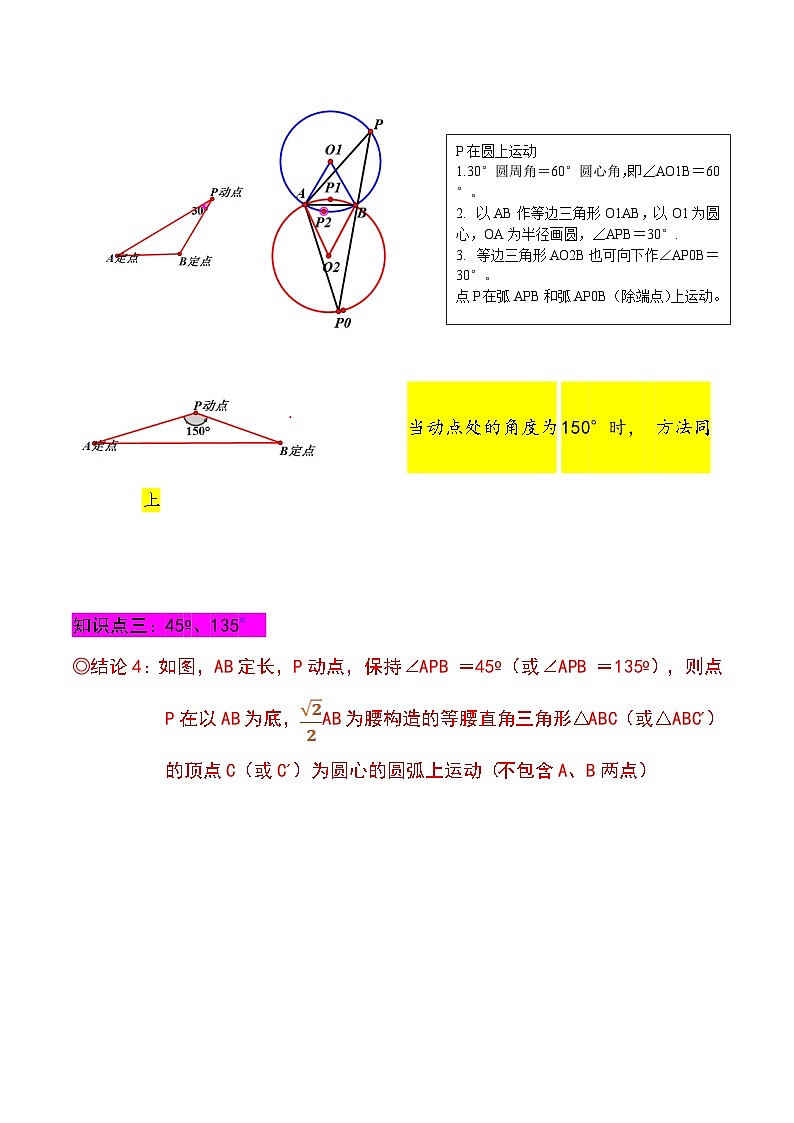
◎结论3：如图，AB定长，P动点，保持∠APB ＝30º（或∠APB ＝150º），则点P在以AB为边构造的等边△ABC（或△ABC´）的顶点C（或C´）为圆心的圆弧上运动（不包含A、B两点）
P在圆上运动
1.30°圆周角＝60°圆心角，即∠AO1B＝60°。
以AB作等边三角形O1AB，以O1为圆心，OA为半径画圆，∠APB＝30°.
等边三角形AO2B也可向下作∠AP0B＝30°。
点P在弧APB和弧AP0B（除端点）上运动。

当动点处的角度为150°时， 方法同上
知识点三：45º、135°
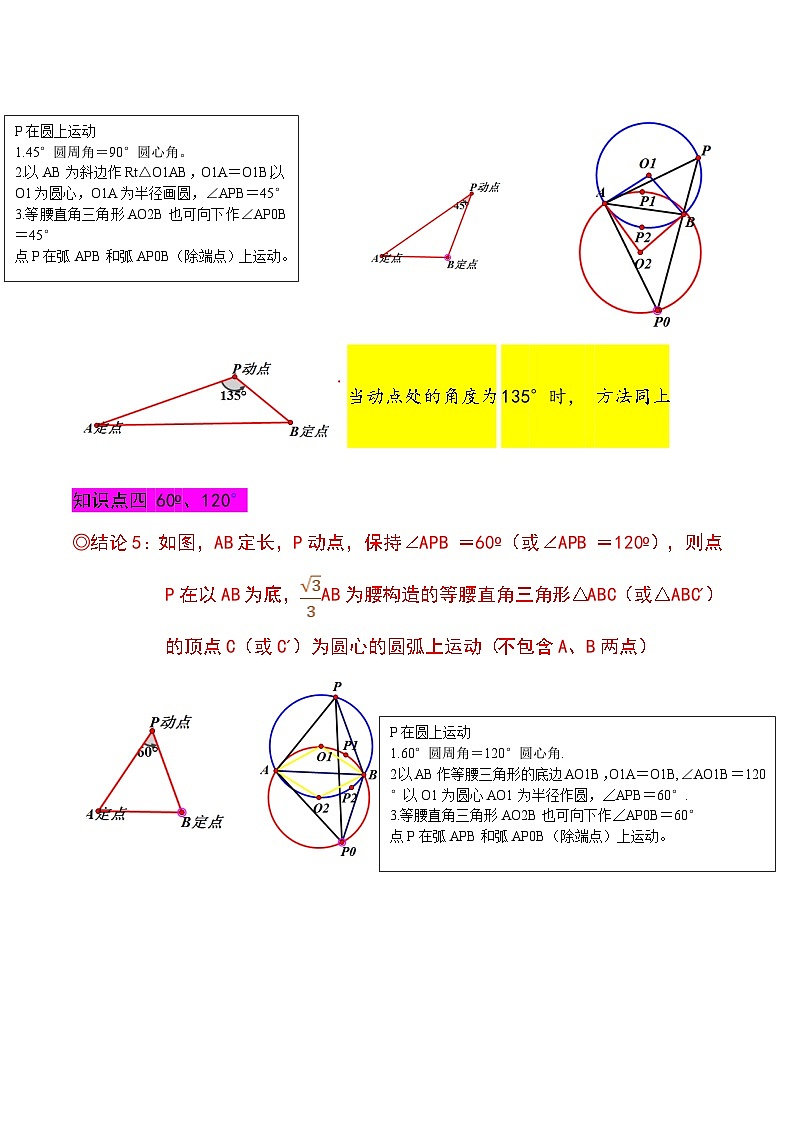
◎结论4：如图，AB定长，P动点，保持∠APB ＝45º（或∠APB ＝135º），则点P在以AB为底，AB为腰构造的等腰直角三角形△ABC（或△ABC´）的顶点C（或C´）为圆心的圆弧上运动（不包含A、B两点）
P在圆上运动
1.45°圆周角＝90°圆心角。
2.以AB为斜边作Rt△O1AB，O1A＝O1B,以O1为圆心，O1A为半径画圆，∠APB＝45°
3.等腰直角三角形AO2B也可向下作∠AP0B＝45°
点P在弧APB和弧AP0B（除端点）上运动。

当动点处的角度为135°时， 方法同上
知识点四 60º、120°
◎结论5：如图，AB定长，P动点，保持∠APB ＝60º（或∠APB ＝120º），则点P在以AB为底，AB为腰构造的等腰直角三角形△ABC（或△ABC´）的顶点C（或C´）为圆心的圆弧上运动（不包含A、B两点）
P在圆上运动
1.60°圆周角＝120°圆心角.
2以AB作等腰三角形的底边AO1B，O1A＝O1B,∠AO1B＝120°以O1为圆心AO1为半径作圆，∠APB＝60°.
3.等腰直角三角形AO2B也可向下作∠AP0B＝60°
点P在弧APB和弧AP0B（除端点）上运动。


当动点处的角度为120°时， 方法同上
1． (2023·全国·九年级专题练习）如图，点在半圆上，半径，，点在弧上移动，连接，作，垂足为，连接，点在移动的过程中，的最小值是______．
2． (2023·四川·成都嘉祥外国语学校九年级阶段练习）如图，在中，，，，过点作的平行线，为直线上一动点，为的外接圆，直线交于点，则的最小值为__________．
1． (2023·江苏·九年级专题练习）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”．如图所示，点、、、分别是“蛋圆”与坐标轴的交点，已知点的坐标为，为半圆的直径，半圆圆心的坐标为，半圆半径为．
（1）求“蛋圆”抛物线部分的解析式及“蛋圆”的弦的长；
（2）已知点是“蛋圆”上的一点（不与点，点重合），点关于轴的对称点是点，若点也在“蛋圆”上，求点坐标；
（3）点是“蛋圆”外一点，满足，当最大时，直接写出点的坐标．
1． (2023·辽宁鞍山·中考真题）如图，抛物线交x轴于点，，D是抛物线的顶点，P是抛物线上的动点，点P的横坐标为，交直线l：于点E，AP交DE于点F，交y轴于点Q．
（1）求抛物线的表达式；
（2）设的面积为，的面积为，当时，求点P的坐标；
（3）连接BQ，点M在抛物线的对称轴上（位于第一象限内），且，在点P从点B运动到点C的过程中，点M也随之运动，直接写出点M的纵坐标t的取值范围．

圆
模型（三十七）——定弦定角模型
定弦定角：线段定，角度大小定
知识点一:
解题步骤：
寻找张角
根据张角动线段、确定隐形圆
定角是圆周角，找圆心，定半径
◎结论1：如图，AB定长，P动点，保持∠APB ＝，则点P在AB所对的圆弧上运动。

◎结论2：90°，如图AB定长，P动点，保持∠APB ＝90º，则点P在以AB为直径的圆弧上运动（不包含A、B两点）

知识点二：30º、150
◎结论3：如图，AB定长，P动点，保持∠APB ＝30º（或∠APB ＝150º），则点P在以AB为边构造的等边△ABC（或△ABC´）的顶点C（或C´）为圆心的圆弧上运动（不包含A、B两点）
P在圆上运动
1.30°圆周角＝60°圆心角，即∠AO1B＝60°。
以AB作等边三角形O1AB，以O1为圆心，OA为半径画圆，∠APB＝30°.
等边三角形AO2B也可向下作∠AP0B＝30°。
点P在弧APB和弧AP0B（除端点）上运动。

当动点处的角度为150°时， 方法同上
知识点三：45º、135
◎结论4：如图，AB定长，P动点，保持∠APB ＝45º（或∠APB ＝135º），则点P在以AB为底，AB为腰构造的等腰直角三角形△ABC（或△ABC´）的顶点C（或C´）为圆心的圆弧上运动（不包含A、B两点）
P在圆上运动
1.45°圆周角＝90°圆心角。
2.以AB为斜边作Rt△O1AB，O1A＝O1B,以O1为圆心，O1A为半径画圆，∠APB＝45°
3.等腰直角三角形AO2B也可向下作∠AP0B＝45°
点P在弧APB和弧AP0B（除端点）上运动。

当动点处的角度为135°时， 方法同上
知识点四 60º、120
◎结论5：如图，AB定长，P动点，保持∠APB ＝60º（或∠APB ＝120º），则点P在以AB为底，AB为腰构造的等腰直角三角形△ABC（或△ABC´）的顶点C（或C´）为圆心的圆弧上运动（不包含A、B两点）
P在圆上运动
1.60°圆周角＝120°圆心角.
2以AB作等腰三角形的底边AO1B，O1A＝O1B,∠AO1B＝120°以O1为圆心AO1为半径作圆，∠APB＝60°.
3.等腰直角三角形AO2B也可向下作∠AP0B＝60°
点P在弧APB和弧AP0B（除端点）上运动。


当动点处的角度为120°时， 方法同上
1． (2023·全国·九年级专题练习）如图，点在半圆上，半径，，点在弧上移动，连接，作，垂足为，连接，点在移动的过程中，的最小值是______．
【答案】
【分析】先确定点H的运动轨迹，再根据点与圆的位置关系可得取最小值时，点H的位置，然后利用圆周角定理、线段的和差即可得．
【详解】如图，设AD的中点为点E，则
由题意得，点H的运动轨迹在以点E为圆心，EA为半径的圆上
由点与圆的位置关系得：连接BE，与圆E交于点H，则此时取得最小值，
连接BD
AB为半圆O的直径
故答案为：．
【点睛】本题考查了圆周角定理、点与圆的位置关系、勾股定理等知识点，依据题意，确定点H的运动轨迹，从而得出BH取最小值时，点H的位置是解题关键．
2． (2023·四川·成都嘉祥外国语学校九年级阶段练习）如图，在中，，，，过点作的平行线，为直线上一动点，为的外接圆，直线交于点，则的最小值为__________．
【答案】2
【分析】如图，连接CE．首先证明∠BEC=120°，根据定弦定角，可得点E在以M为圆心，MB为半径的上运动，连接MA交于E′，此时AE′的值最小．
【详解】解：如图，连接CE．
∵AP∥BC，
∴∠PAC=∠ACB=60°，
∴∠CEP=∠CAP=60°，
∴∠BEC=120°，
,为定值，则点E的运动轨迹为一段圆弧
如图，点E在以M为圆心，MB为半径的上运动，过点作
∴中优弧度数为=240°，则劣弧度数为120°
∴△BMC是等腰三角形，∠BMC=120°，
∵∠BCM=30°，BC=，
∴MB=MC=8，
∴连接MA交于E′，此时AE′的值最小．
∵∠ACB=60°，∠BCO=30°，
∴∠ACM=90°，
∴MA==，
∴AE的最小值为=．
故答案为：2
【点睛】本题考查三角形的外接圆与外心、平行线的性质、圆周角定理、勾股定理，点与圆的位置关系等知识，解题的关键是添加常用辅助线，构造辅助圆解决问题．
1． (2023·江苏·九年级专题练习）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”．如图所示，点、、、分别是“蛋圆”与坐标轴的交点，已知点的坐标为，为半圆的直径，半圆圆心的坐标为，半圆半径为．
（1）求“蛋圆”抛物线部分的解析式及“蛋圆”的弦的长；
（2）已知点是“蛋圆”上的一点（不与点，点重合），点关于轴的对称点是点，若点也在“蛋圆”上，求点坐标；
（3）点是“蛋圆”外一点，满足，当最大时，直接写出点的坐标．
【答案】（1）“蛋圆”抛物线部分的解析式为，CD的长；（2）E1(，1)，E2(，1)，E3(，−1)，E4(，−1)；（3）点P的坐标为（1，）．
【分析】（1）求出点A，B的坐标，运用待定系数法求出函数解析式；将x=0代入抛物线的解析式得y=-3，故此可得到DO的长，可得到AB的长，由M为圆心可得到MC和OM的长，然后依据勾股定理可求得OC的长，最后依据CD=OC+OD求解即可．
（2）假设点E在x轴上方的“蛋圆”上，EF与x轴交于点H，连接EM．由HM2+EH2=EM2，点F在二次函数y=x2-2x-3的图象上，可得方程组，以及对称性求解；
（3）根据∠BPC=60°保持不变，点P在一圆弧上运动和直径是最大的弦进行解答即可．
【详解】解：（1）∵圆心的坐标为，半圆半径为2．
∴A（-1，0），B（3，0）
设“蛋圆”抛物线部分的解析式为
把A（-1，0），B（3，0），D（0，-3）代入解析式得，

解得，
∴“蛋圆”抛物线部分的解析式为
连接AC，BC，MC
∵点D的坐标为（0，-3），
∴OD的长为3．
∵A（-1，0），B（3，0）．
∴AO=1，BO=3，AB=4，
∵M（1，0）．
∴MC=2，OM=1．
在Rt△COM中，OC=．
∴CD=CO+OD=，即这个“蛋圆”被y轴截得的线段CD的长．
（2）假设点E在x轴上方的“蛋圆”上，设E（m，n），则点F的坐标为（m，-n）．
EF与x轴交于点H，连接EM．
∴HM2+EH2=EM2，
∴（m-1）2+n2=4，…①；
∵点F在二次函数y=x2-2x-3的图象上，
∴m2-2m-3=-n，…②
解由①②组成的方程组得：；．（n=0舍去）
由对称性可得：；．
∴E1(，1)，E2(，1)，E3(，−1)，E4(，−1)．
（3）如图，
∵∠BPC=60°保持不变，
因此点P在一圆弧上运动．
此圆是以K为圆心（K在BC的垂直平分线上，且∠BKC=120°），BK为半径．
当BP为直径时，BP最大．
在中，
∴，
∴
∴
∵
∴
在中，
∴
∴
在Rt△PCR中，
∴
∴
∴
∴点P的坐标为（1，）．
【点睛】本题考查的是圆与二次函数知识的综合运用，正确理解“蛋圆”的概念、掌握圆周角定理、二次函数的图象和性质、灵活运用数形结合思想是解题的关键，解答时，注意辅助线的作法要正确．
1． (2023·辽宁鞍山·中考真题）如图，抛物线交x轴于点，，D是抛物线的顶点，P是抛物线上的动点，点P的横坐标为，交直线l：于点E，AP交DE于点F，交y轴于点Q．
（1）求抛物线的表达式；
（2）设的面积为，的面积为，当时，求点P的坐标；
（3）连接BQ，点M在抛物线的对称轴上（位于第一象限内），且，在点P从点B运动到点C的过程中，点M也随之运动，直接写出点M的纵坐标t的取值范围．

【答案】（1）；（2）；（3）．
【分析】（1）运用待定系数法将，代入，即可求得答案；
（2）利用配方法可求得抛物线顶点坐标，由得，再根据与的面积相等，可得，故点F分别是AP、ED的中点，设，，结合中点坐标公式建立方程求解即可；
（3）根据题意，分别求出t的最大值和最小值：①当点P与点B重合时，点Q与点O重合，此时t的值最大，如图2，以OB为斜边在第一象限内作等腰直角，以为圆心，为半径作，交抛物线对称轴于点，过点作轴于点H，运用勾股定理即可求得答案，②当点P与点C重合时，点Q与点C重合，此时t的值最小，如图3，连接BC，以O为圆心，OB为半径作交抛物线对称轴于点M，连接OM，设抛物线对称轴交x轴于点E，运用勾股定理即可求得答案．
【详解】解：（1）抛物线交x轴于点，，
将A、B坐标分别代入抛物线解析式得：，
解得：，
抛物线的表达式为：；
（2）如图，
D是抛物线的顶点，抛物线的表达式为：，
，
交直线l：于点E，P是抛物线上的动点，点P的横坐标为，
，设，，
又的面积为，的面积为，，
，
，，即点F分别是AP、ED的中点，
又，，，，
由中点坐标公式得：，
解得：（与“”不符，应舍去），，
，
，；
（3）①当点P与点B重合时，点Q与点O重合，此时t的值最大，如图2，
以OB为斜边在第一象限内作等腰直角，
则，，
以为圆心，为半径作，交抛物线对称轴于点，
过点作轴于点H，则，，，
，
，
②当点P与点C重合时，点Q与点C重合，此时t的值最小，如图3，
连接BC，以O为圆心，OB为半径作交抛物线对称轴于点M，
，
经过点C，
连接OM，设抛物线对称轴交x轴于点E，
则，，
，
，
，
综上所述，．
【点睛】此题属于二次函数综合题，考查代数计算问题，涉及勾股定理，三角形全等，二元一次方程和一元二次方程的解及圆的相关知识，属于压轴题类型．