专题六　第4讲　母题突破3　定值问题--高三高考数学复习-PPT

这是一份专题六　第4讲　母题突破3　定值问题--高三高考数学复习-PPT，共46页。PPT课件主要包含了母题突破3，定值问题，因为A0－1，规律方法，1求C的方程，专题强化练，因为H为NG的中点，即m2＝2k2＋2等内容，欢迎下载使用。
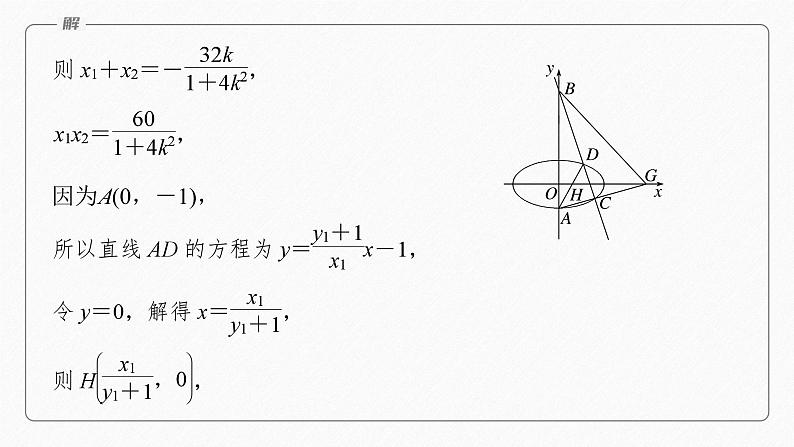
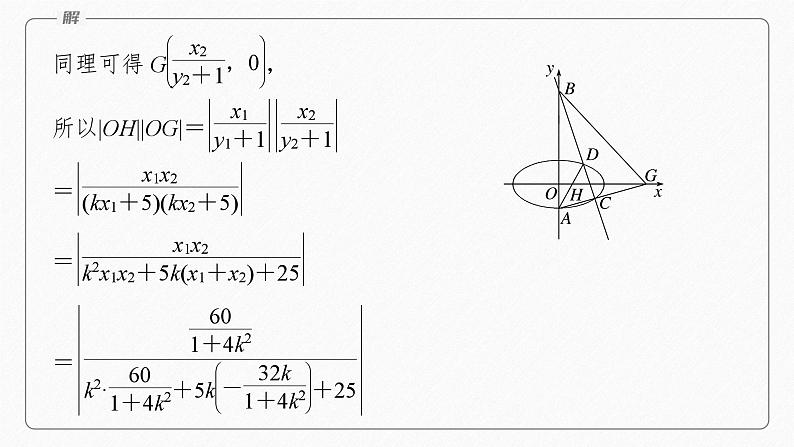
(1)求椭圆E的方程；(2)如图，过点B(0,4)作一条与y轴不重合的直线，该直线交椭圆E于C，D两点，直线AD，AC分别交x轴于H，G两点，O为坐标原点.证明：|OH||OG|为定值，并求出该定值.
思路分析❶结合点的坐标和AM的斜率列方程组❷设直线BC的方程并与椭圆的方程联立❸得到x1＋x2，x1x2❹写出直线AD，AC的方程并求出H，G的横坐标❺化简运算|OH||OG|
(2)由题意知，直线BC的斜率存在，设直线BC：y＝kx＋4，设D(x1，y1)，C(x2，y2)，
得(1＋4k2)x2＋32kx＋60＝0，Δ＝(32k)2－4(1＋4k2)×60＝16(4k2－15)＞0，
　　(2023·西安模拟)如图，在平面直角坐标系中，椭圆E：　　＝1，A，B分别为椭圆E的左、右顶点.已知图中四边形ABCD是矩形，且|BC|＝4，点M，N分别在边BC，CD上，AM与BN相交于第一象限内的点P.若点P在椭圆E上，证明：　 为定值，并求出该定值.
设P(x0，y0)(x0>0，y0>0)，M(xM，yM)，N(xN，yN)，
　　(2023·衡水质检)已知E(2,2)是抛物线C：y2＝2x上一点，经过点(2,0)的直线l与抛物线C交于A，B两点(不同于点E)，直线EA，EB分别交直线x＝－2于点M，N.已知O为原点，求证：∠MON为定值.
设直线l的方程为x＝my＋2，
消去x，整理得y2－2my－4＝0，Δ＝4m2＋16>0恒成立.则y1y2＝－4，y1＋y2＝2m，
求解定值问题的两大途径(1)由特例得出一个值(此值一般就是定值)→证明定值：将问题转化为证明待证式与参数(某些变量)无关.(2)先将式子用动点坐标或动线中的参数表示，再利用其满足的约束条件使其绝对值相等的正负项抵消或分子、分母约分得定值.
1.已知抛物线C：y2＝2px(p>0)，F为其焦点，若圆E：(x－1)2＋y2＝16与抛物线C交于A，B两点，且|AB|＝　　(1)求抛物线C的方程；
由题意可知E(1,0)，半径r＝4，由圆的圆心以及抛物线的焦点均在x轴上以及对称性可知AB⊥x轴于点C，如图所示，在Rt△ACE中，
因此|OC|＝|OE|＋|CE|＝3，
12＝6p⇒p＝2，故抛物线方程为y2＝4x.
(2)若点P为圆E上任意一点，且过点P可以作抛物线C的两条切线PM，PN，切点分别为M，N.求证：|MF|·|NF|恒为定值.
如图所示，令P(x0，y0)，M(x1，y1)，N(x2，y2)，抛物线在点M处的切线方程为x－x1＝m(y－y1)，与y2＝4x联立得y2－4my＋4my1－4x1＝0，①由相切得Δ＝16m2－4(4my1－4x1)＝0，得4my1－4x1＝4m2，代入①得y1＝2m，
即为yy1＝2x＋2x1，
同理在点N处的切线方程为yy2＝2x＋2x2，而两切线交于点P(x0，y0)，所以有y0y1＝2x0＋2x1，y0y2＝2x0＋2x2，则直线MN的方程为2x－y0y＋2x0＝0，
得y2－2y0y＋4x0＝0，所以y1＋y2＝2y0，y1y2＝4x0，于是|MF|·|NF|＝(x1＋1)(x2＋1)
又点P(x0，y0)在圆E：(x－1)2＋y2＝16上，
即|MF|·|NF|＝16.
因为c2，a2，b2成等差数列，所以2a2＝c2＋b2，又c2＝a2＋b2，所以a2＝2b2.
(2)过F的直线与C的右支交于P，Q两点(P在Q的上方)，PQ的中点为M，M在直线l：x＝2上的射影为N，O为坐标原点，设△POQ的面积为S，直线PN，QN的斜率分别为k1，k2，证明： 是定值.
依题意可设PQ：x＝my＋3，
得(m2－2)y2＋6my＋3＝0，如图，设P(x1，y1)，Q(x2，y2)，y1>y2，
则k1－k2＝kPN－kQN
所以C的方程为x2－y2＝1.
(2)过点P作直线l交C于M，N两点，过点N作x轴的垂线交直线AM于点G，H为NG的中点，证明：直线AH的斜率为定值.
当直线l的斜率不存在时，直线l与双曲线只有一个交点，不符合题意，当直线l的斜率存在时，设直线l的方程为y－1＝k(x－1)，M(x1，y1)，N(x2，y2)，
消去y得(1－k2)x2－2k(1－k)x－k2＋2k－2＝0，则1－k2≠0，且Δ＝4k2(1－k)2－4(1－k2)(－k2＋2k－2)＝8－8k>0，解得k