专题六　微重点11　圆锥曲线中二级结论的应用--高三高考数学复习-PPT

这是一份专题六　微重点11　圆锥曲线中二级结论的应用--高三高考数学复习-PPT，共60页。PPT课件主要包含了考点一，考点二，焦点弦问题，等角的性质，考点三，切点弦方程，专题强化练，核心提炼，图1图2，又因为x0≥1等内容，欢迎下载使用。
圆锥曲线是高中数学的重要内容之一，知识的综合性较强，因而解题时需要运用多种基础知识，采用多种数学手段，熟记各种定义、基本公式.法则固然很重要，但要做到迅速、准确地解题，还要掌握一些常用结论，理解各结论之间的联系与区别，正确灵活地运用这些结论，一些复杂的问题便能迎刃而解.
1.已知F1，F2分别为椭圆的左、右焦点，直线 l过左焦点F1与椭圆(焦点在x轴上)交于A，B两点，设 ∠AF1F2＝α，e为椭圆的离心率，p为椭圆的焦点到对应准线的距离，则p＝
(3)焦点三角形的面积公式：P为椭圆上异于长轴端点的一点，F1，F2为其左、右焦点且∠F1PF2＝θ，则 ＝b2·tan .
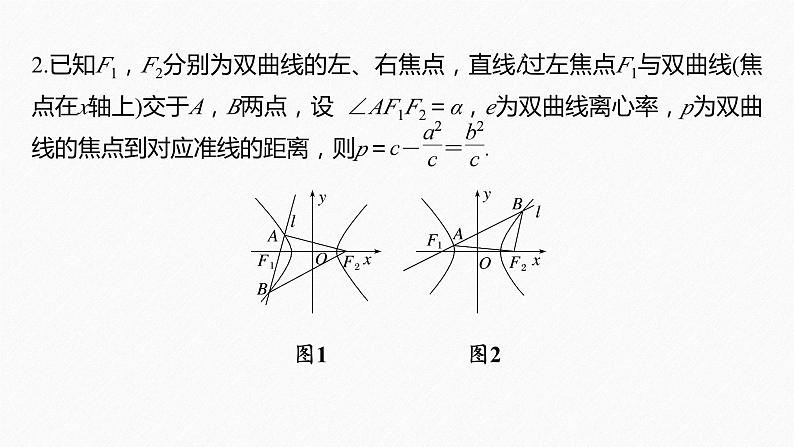
2.已知F1，F2分别为双曲线的左、右焦点，直线l过左焦点F1与双曲线(焦点在x轴上)交于A，B两点，设 ∠AF1F2＝α，e为双曲线离心率，p为双曲线的焦点到对应准线的距离，则p＝
(3)焦点三角形的面积公式：P为双曲线上异于实轴端点的一点，F1，F2为其左、右焦点且∠F1PF2＝θ，则 ＝
3.已知直线l过焦点F与抛物线(焦点在x轴上)交于A，B两点，设 ∠AFx＝α，e为抛物线离心率，p为抛物线的焦点到对应准线的距离.
　　(2023·滨州模拟)过椭圆T: ＋y2＝1上的焦点F作两条互相垂直的直线l1，l2，l1交椭圆于A，B两点，l2交椭圆于C，D两点，则|AB|＋|CD|的取值范围是
方法一　不妨设直线l1的倾斜角小于直线l2的倾斜角，则直线l1的倾斜角为θ，直线l2的倾斜角为 ＋θ，
所以 0≤sin 2θ≤1，所以8≤8＋sin22θ≤9，
方法二　当直线l1，l2有一条斜率不存在时，不妨设直线l1的斜率不存在，则直线l2的斜率为0，
不妨设直线l1，l2都过椭圆的右焦点F(1,0)，
可得(1＋2k2)x2－4k2x＋2k2－2＝0，Δ＝(－4k2)2－4(1＋2k2)(2k2－2)＝8k2＋8>0，
令1＋k2＝t，因为k≠0，所以t>1，
要注意公式中α的含义.(2)公式中的加减符号易混淆.(3)直线与双曲线交于一支和两支的公式不一样.
　　　已知双曲线x2－y2＝2，点F1，F2为其左、右焦点，点P为双曲线上一点，若∠F1PF2＝60°，则△F1PF2的面积为
3.已知抛物线y2＝2px(p>0)，过抛物线对称轴上任意一点N(a,0)的一条弦的端点A，B与对应点G(－a,0)的连线所成角被对称轴平分，即∠OGA＝∠OGB(如图3).
　　(2023·洛阳模拟)在平面直角坐标系Oxy中，曲线C：x2＝6y与直线l：y＝kx＋3交于M，N两点.(1)当10，设A(x1，y1)，B(x2，y2)，
假设存在定点Q(0，t)(t≠1)符合题意，∵∠PQA＝∠PQB，∴kQA＝－kQB，
∵上式对任意实数k恒等于零，∴4－t＝0，即t＝4，∴Q(0,4)，当直线l的斜率不存在时，A，B(不妨设点A在x轴上方)两点分别为椭圆的上下顶点(0,2)，(0，－2)，显然此时∠PQA＝∠PQB，综上，存在定点Q(0,4)满足题意.
(1)证明：Q是线段MN的中点；
得3x2＋6x－25＝0.设M(x1，y1)，N(x2，y2)，则x1，x2是方程的两根，故x1＋x2＝－2.
故Q(－1，－1)是线段MN的中点.
(2)分别过点M，N作双曲线的切线l1，l2，证明：三条直线l，l1，l2相交于同一点；
(3)设P为直线l上一动点，过P作双曲线的切线PA，PB，切点分别为A，B，证明：点Q在直线AB上.
设P(x0，y0)，A(x3，y3)，B(x4，y4)，则PA，PB的方程分别为
显然，无论x0取什么值(即无论P为直线l上哪一点)，点Q(－1，－1)都在直线AB上.
运用联想，由过已知圆上和圆外的点的切线方程联想到过圆锥曲线上和圆锥曲线外的切线方程，触类旁通，实现知识的内迁，使知识更趋于系统化，取得事半功倍的效果.
(1)求证：直线AB过定点M，并求出定点M的坐标；
又因为a2＝b2＋c2，
设A(x1，y1)，B(x2，y2)，P(3，y0)，
因为点P在直线PA，PB上，
(2)记△AFM，△BFM的面积分别为S1和S2，当|S1－S2|取最大值时，求直线AB的方程.
设直线AB的方程为x＝ty＋2，
得(t2＋3)y2＋4ty－2＝0，
A.1 　　　B.2 　　　 C.4 　　 D.8
根据焦点三角形面积公式可知，
结合c2＝a2＋b2，解得a＝1.
2.已知抛物线C的顶点在坐标原点，准线方程为x＝－1，过其焦点F的直线l与抛物线C交于A，B两点，若直线l的斜率为1，则弦AB的长为A.4 　　　B.6 　　　C.7 　　　 D.8
∵k＝tan θ＝1，
3.(2023·齐齐哈尔模拟)已知椭圆C： 　　＝1(a>b>0)的左、右焦点分别为F1，F2.若椭圆C上存在一点M，使得|F1F2|是|MF1|与|MF2|的等比中项，则椭圆C的离心率的取值范围是
设椭圆C上存在一点M(m，n)，由椭圆的第二定义，可得|MF1|＝a＋em，|MF2|＝a－em，由|F1F2|是|MF1|与|MF2|的等比中项，可得|F1F2|2＝|MF1||MF2|，即4c2＝(a＋em)(a－em)，即e2m2＝a2－4c2，因为0≤m2≤a2，所以0≤e2m2≤a2e2,0≤a2－4c2≤a2e2，
对于C，当点A为短轴的一个顶点时，∠F1AF2最大，
所以∠F1AF2为锐角，
6.(多选)(2023·襄阳模拟)如图，过双曲线C：x2－ ＝1(b>0)右支上一点P作双曲线的切线l分别交两渐近线于A，B两点，交x轴于点D，F1，F2分别为双曲线的左、右焦点，O为坐标原点，则下列结论正确的是A.|AB|min＝2bB.S△OAP＝S△OBPC.S△AOB＝2b
则双曲线C的离心率e＝2
设点P(x0，y0)，A(x1，y1)是切线与渐近线在第一象限的交点，B(x2，y2)是切线与渐近线在第四象限的交点，双曲线的渐近线方程为y＝±bx，
即|AB|min＝2b，故A项正确；
所以点P(x0，y0)是A，B的中点，所以S△OAP＝S△OBP，故B项正确；
则S△AOB＝S△AOD＋S△BOD
所以2a＝|PF1|－|PF2|＝4－2＝2，解得a＝1，
解得c2＝4，所以c＝2，
方法一　设l1，l2的倾斜角分别为α，β，
方法二　设直线AB的方程为y＝k1(x＋2)，A(x1，y1)，B(x2，y2)，
线的倾斜角为120°，则双曲线的离心率为______.
方法一　设|AF1|＝k，|BF1|＝7k，根据双曲线定义|AF2|＝k＋2a，|BF2|＝7k＋2a，在△AF1F2中，由余弦定理可得(k＋2a)2＝(2c)2＋k2－2·2c·kcs 60°，在△BF1F2中，由余弦定理可得(7k＋2a)2＝(7k)2＋(2c)2－2·2c·7kcs 120°，
(2)在x轴上是否存在一点M，使得过F的任意一条直线l与椭圆的两个交点A，B，恒有∠OMA＝∠OMB，若存在求出M的坐标，若不存在，说明理由.
由(1)知，F(1,0)，假定存在点M(t,0)满足条件，当直线与x轴不重合时，设l的方程为x＝my＋1，
消去x并整理得(m2＋2)y2＋2my－1＝0，设A(x1，y1)，B(x2，y2)，
因为∠OMA＝∠OMB，则直线MA，MB的斜率互为相反数，
整理得y1(my2＋1－t)＋y2(my1＋1－t)＝0，即2my1y2＋(1－t)(y1＋y2)＝0，
当直线l与x轴重合时，点A，B为椭圆长轴的两个端点，点M(2,0)也满足∠OMA＝∠OMB，综上，存在点M满足条件，点M的坐标为(2,0).
(1)求椭圆E的方程；
(2)M是直线x＝4上任意一点，过M作椭圆E的两条切线MA，MB(A，B为切点).①求证：MF2⊥AB；
设A(xA，yA)，B(xB，yB)，M(4，t).
又直线AM，BM过点M(4，t)，
故点A(xA，yA)，B(xB，yB)在直线3x＋ty＝3上，故直线AB方程为3x＋ty＝3，当t＝0，即M(4,0)时，直线AB方程为x＝1，则MF2⊥AB.
②求△MAB面积的最小值.
将直线AB方程3x＋ty＝3与椭圆E的方程联立得(t2＋12)y2－6ty－27＝0，
∵其在m∈[3，＋∞)上单调递增，