湖南省永州市李达中学2023-2024学年九年级下学期开学测试数学试题(无答案)

这是一份湖南省永州市李达中学2023-2024学年九年级下学期开学测试数学试题(无答案)，共6页。试卷主要包含了单选题，四象限，则的值可以是，解答题等内容，欢迎下载使用。

一、单选题（每小题3分，共30分）
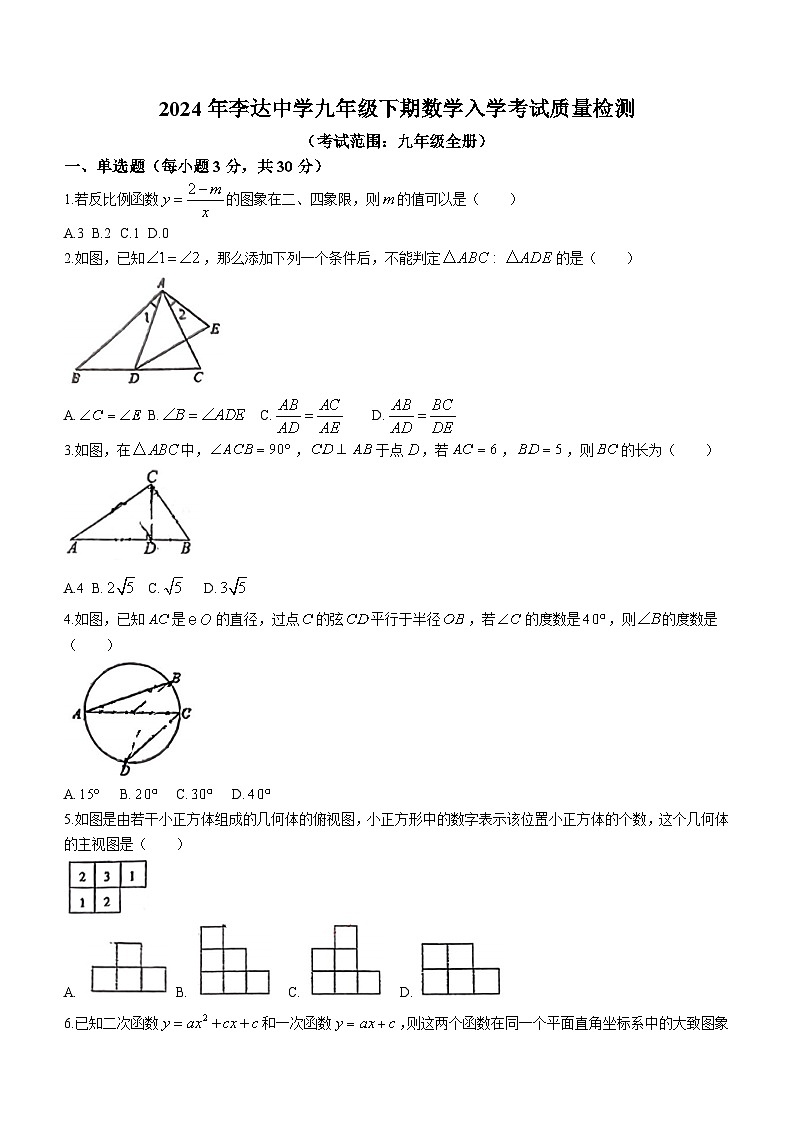
1.若反比例函数的图象在二、四象限，则的值可以是（ ）
A.3B.2C.1D.0
2.如图，已知，那么添加下列一个条件后，不能判定的是（ ）
A.B.C.D.
3.如图，在中，，于点，若，，则的长为（ ）
A.4B.C.D.
4.如图，已知是的直径，过点的弦平行于半径，若的度数是，则的度数是（ ）
A.B.C.D.
5.如图是由若干小正方体组成的几何体的俯视图，小正方形中的数字表示该位置小正方体的个数，这个几何体的主视图是（ ）
A. B. C. D.
6.已知二次函数和一次函数，则这两个函数在同一个平面直角坐标系中的大致图象是（ ）
A. B. C. D.
7.如图，小芳在地面上放置一个平面镜来测量铁塔的高度，镜子与铁塔的距离米，镜与小芳的距离米时，小芳刚好从镜子中看到铁塔顶端，已知小芳的眼睛距地面的高度1.5米，铁塔的高度为（ ）（根据光的反射原理，）
A.18mB.15mC.20mD.16m
8.已知，是方程的两根，则代数式的值是（ ）
A.19B.20C.14D.15
9.二次函数的图像的一部分如图所示，已知图像经过点，其对称轴为直线.下列结论：①；②；③；④点是抛物线上的两点，若，则；⑤若抛物线经过点，则关于的一元二次方程的两根分别为-3，5；其中正确的有（ ）
A.2个B.3个C.4个D.5个
10.如图，，，，…是分别以，，，…为直角顶点，一条直角边在轴正半轴上的等腰直角三角形，其斜边的中点，，，…均在反比例函数的图象上，则的值为（ ）
A.B.16C.8D.17
二、填空题（每小题3分，共24分）
11.已知点，，都在反比例函数（为常数，且）的图象上，则，，之间的大小关系是________.（用“<”连接）
12.如图，已知正方形的顶点、在的边上，顶点、分别在边、上.如果，的面积是6，那么这个正方形的边长是________.
13.如图，在的方格中，两条线段的夹角（锐角）为，则________.
14.如图，是的切线，为切点，经过点，与分别相交于点，，若，，则阴影部分的面积是________.
15.如图，在矩形中，，，点在上，将矩形沿折叠，点恰好落在边上的点处，那么的值是________.
16.如图，点在双曲线上，点在双曲线上，轴，过点作轴于.连接，与相交于点，若，则的值为________.
17.一个物体的三视图如图所示，其中主视图和左视图是全等的等边三角形，俯视图是圆，根据图中所示数据，可求这个物体的表面积是________.
18.关于的一元二次方程的两个实数根是，，满足，则的取值范围是________.
三、解答题（本大题共8个小题，共66分）
19.计算： 解方程：
20.以“光盘”为主题的公益活动越来越受到社会的关注.某校为培养学生勤俭节约的习惯，随机抽查了部分学生（态度分为：赞成、无所谓、反对），并将抽查结果绘制成图1和图2（统计图不完整）.请根据图中提供的信息，解答下列问题：
图1 图2
（1）此次抽样调查中，共抽查了________名学生；
（2）将图1补充完整；
（3）根据抽样调查结果，请你估计该校3000名学生中有多少名学生持反对态度？
21.如图，已知反比例函数的图象与一次函数的图象于点和点，直线交轴于点.
（1）求这两个函数的关系式；
（2）求的面积；
（3）结合图象直接写出时，的取值范围.
22.若关于的一元二次方程.
（1）求证：方程总有两个实数根；
（2）若方程的两个实数根分别为，，且，求的值.
23.高考英语听力测试期间，需要杜绝考点周围的噪音.如图，点是某市一高考考点，在位于考点南偏西方向距离125米的点处有一消防队.在听力考试期间，消防队突然接到报警电话，告知在位于点北偏东方向的点处突发火灾，消防队必须立即赶往救火.已知消防车的警报声传播半径为100米，若消防车的警报声对听力测试造成影响，则消防车必须改道行驶.
试问：消防车是否需要改道行驶？说明理由.（取1.732）
24.2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行，冬奥会吉祥物为“冰墩墩”.
（1）据市场调研发现，某工厂今年二月份共生产500个“冰墩墩”，为增大生产量，该工厂平均每月生产量增加20％，则该工厂在四月份能生产多少个“冰墩墩”？
（2）已知某商店“冰墩墩”平均每天可销售20个，每个盈利40元，在每个降价幅度不超过10元的情况下，每下降2元，则每天可多售10件，如果每天要盈利1440元，则每个“冰墩墩”应降价多少元？
25.如图，是的直径，是弦，直线经过点，于点，.
（1）求证：是的切线；
（2）求证：；
（3）若的半径为4，，求图中阴影部分的面积.
26.如图，抛物线与轴交于，两点，且，与轴交于.直线与抛物线交于，两点，与轴交于点，设直线上方的抛物线上的动点的横坐标为.
（1）求该抛物线的解析式和顶点坐标；
（2）连接，，当为何值时，；
（3）在直线上是否存在一点，使得为等腰直角三角形？若存在，请直接写出点的坐标；若不存在，请你说明理由.