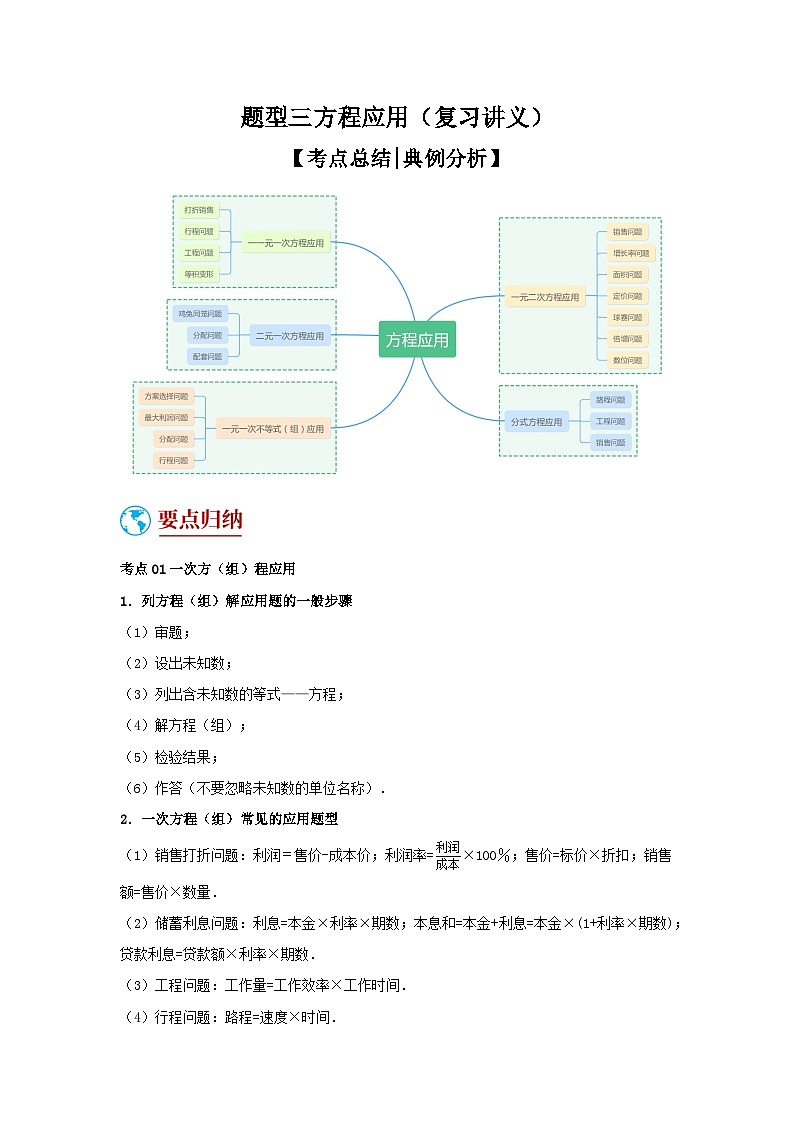
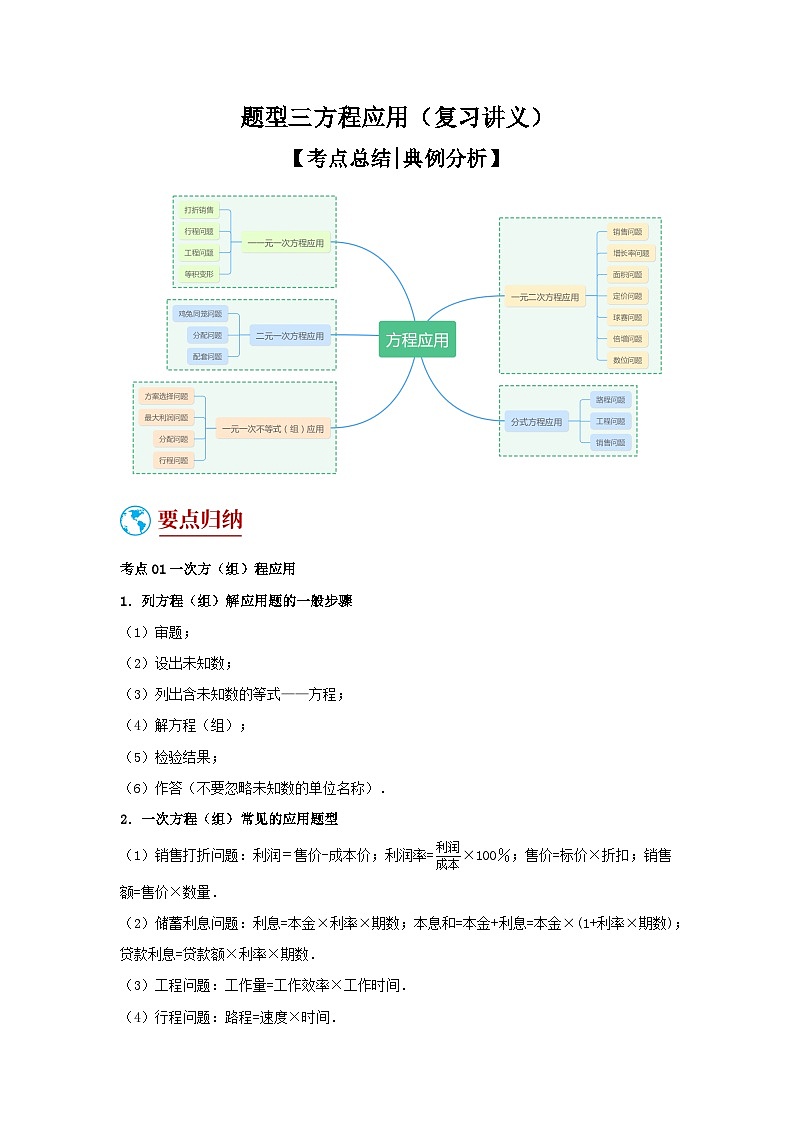
题型三 方程应用（复习讲义）(一元一次方程、二元一次方程、一元一次不等式、分式方程、一元二次方程应用)-备战2024年中考数学二轮复习高分突破（全国通用）

这是一份题型三 方程应用（复习讲义）(一元一次方程、二元一次方程、一元一次不等式、分式方程、一元二次方程应用)-备战2024年中考数学二轮复习高分突破（全国通用），文件包含题型三方程应用复习讲义一元一次方程二元一次方程一元一次不等式分式方程一元二次方程应用原卷版docx、题型三方程应用复习讲义一元一次方程二元一次方程一元一次不等式分式方程一元二次方程应用解析版docx等2份试卷配套教学资源，其中试卷共44页， 欢迎下载使用。

考点01一次方（组）程应用
1．列方程（组）解应用题的一般步骤
（1）审题；
（2）设出未知数；
（3）列出含未知数的等式——方程；
（4）解方程（组）；
（5）检验结果；
（6）作答（不要忽略未知数的单位名称）．
2．一次方程（组）常见的应用题型
（1）销售打折问题：利润售价-成本价；利润率=×100％；售价=标价×折扣；销售额=售价×数量．
（2）储蓄利息问题：利息=本金×利率×期数；本息和=本金+利息=本金×(1+利率×期数)；贷款利息=贷款额×利率×期数．
（3）工程问题：工作量=工作效率×工作时间．
（4）行程问题：路程=速度×时间．
（5）相遇问题：全路程=甲走的路程+乙走的路程．
（6）追及问题（同地不同时出发）：前者走的路程=追者走的路程．
（7）追及问题（同时不同地出发）：前者走的路程+两地间距离=追者走的路程．
（8）水中航行问题：顺水速度=静水速度+水流速度；逆水速度=静水速度-水流速度．
1.（2022·山东泰安）泰安某茶叶店经销泰山女儿茶，第一次购进了A种茶30盒，B种茶20盒，共花费6000元；第二次购进时，两种茶每盒的价格都提高了20%，该店又购进了A种茶20盒，B种茶15盒，共花费5100元．求第一次购进的A、B两种茶每盒的价格．
【答案】A种茶每盒100元，B种茶每盒150元
【分析】设第一次购进A种茶每盒x元，B种茶每盒y元，根据第一次购进了A种茶30盒，B种茶20盒，共花费6000元；第二次购进时，两种茶每盒的价格都提高了20%，该店又购进了A种茶20盒，B种茶15盒，共花费5100元列出方程组求解即可．
【详解】解：设第一次购进A种茶每盒x元，B种茶每盒y元，
根据题意，得解，得
A种茶每盒100元，B种茶每盒150元．
【点睛】本题主要考查了二元一次方程组的实际应用，正确设出未知数列出方程组求解是解题的关键．
2．（2022·湖南常德）小强的爸爸平常开车从家中到小强奶奶家，匀速行驶需要4小时，某天，他们以平常的速度行驶了的路程时遇到了暴雨，立即将车速减少了20千米／小时，到达奶奶家时共用了5小时，问小强家到他奶奶家的距离是多少千米？
【答案】240千米
【分析】平常速度行驶了的路程用时为2小时，后续减速后用了3小时，用遇到暴雨前行驶路程加上遇到暴雨后行驶路程等于总路程这个等量关系列出方程求解即可．
【详解】解：设小强家到他奶奶家的距离是千米，则平时每小时行驶千米，减速后每小时行驶千米，由题可知：遇到暴雨前用时2小时，遇到暴雨后用时5-2=3小时，
则可得：，解得：，
答：小强家到他奶奶家的距离是240千米．
【点睛】本题考查了一元一次方程应用中的行程问题，直接设未知数法，找到准确的等量关系，列出方程正确求解是解题的关键．
3.（2021·重庆中考真题）重庆小面是重庆美食的名片之一，深受外地游客和本地民众欢迎．某面馆向食客推出经典特色重庆小面，顾客可到店食用（简称“堂食”小面），也可购买搭配佐料的袋装生面（简称“生食”小面）．已知3份“堂食”小面和2份“生食”小面的总售价为31元，4份“堂食”小面和1份“生食”小面的总售价为33元．
（1）求每份“堂食”小面和“生食”小面的价格分别是多少元？
（2）该面馆在4月共卖出“堂食”小面4500份，“生食”小面2500份，为回馈广大食客，该面馆从5月1日起每份“堂食”小面的价格保持不变，每份“生食”小面的价格降低．统计5月的销量和销售额发现：“堂食”小面的销量与4月相同，“生食”小面的销量在4月的基础上增加，这两种小面的总销售额在4月的基础上增加．求a的值．
【答案】（1）每份“堂食”小面价格是7元，“生食”小面的价格是5元．（2）a的值为8．
【分析】
（1）设每份“堂食”小面和“生食”小面的价格分别是x、y元，根据题意列出二元一次方程组，解方程组即可；
（2）根据题意列出一元二次方程，解方程即可．
【详解】
解：（1）设每份“堂食”小面和“生食”小面的价格分别是x、y元，根据题意列方程组得，，
解得，，
答：每份“堂食”小面价格是7元，“生食”小面的价格是5元．
（2）根据题意得，，
解得，（舍去），，
答：a的值为8．
【点睛】
本题考查了二元一次方程组的应用和一元二次方程的应用，解题关键是找准题目中的等量关系，列出方程，熟练运用相关知识解方程．
4.（2020•安徽）某超市有线上和线下两种销售方式．与2019年4月份相比，该超市2020年4月份销售总额增长10%，其中线上销售额增长43%，线下销售额增长4%．
（1）设2019年4月份的销售总额为a元，线上销售额为x元，请用含a，x的代数式表示2020年4月份的线下销售额（直接在表格中填写结果）；
（2）求2020年4月份线上销售额与当月销售总额的比值．
【分析】
（1）由线下销售额的增长率，即可用含a，x的代数式表示出2020年4月份的线下销售额；
（2）根据2020年4月份的销售总额＝线上销售额+线下销售额，即可得出关于x的一元一次方程，解之即可得出x的值（用含a的代数式表示），再将其代入中即可求出结论．
【解析】
（1）∵与2019年4月份相比，该超市2020年4月份线下销售额增长4%，
∴该超市2020年4月份线下销售额为1.04（a﹣x）元．
故答案为：1.04（a﹣x）．
（2）依题意，得：1.1a＝1.43x+1.04（a﹣x），
解得：x=213，
∴⋅213a1.1a=．
答：2020年4月份线上销售额与当月销售总额的比值为0.2．
5.（2020•江西）放学后，小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本，这种笔芯每盒10支，如果整盒买比单支买每支可优惠0.5元．小贤要买3支笔芯，2本笔记本需花费19元；小艺要买7支笔芯，1本笔记本需花费26元．
（1）求笔记本的单价和单独购买一支笔芯的价格；
（2）小贤和小艺都还想再买一件单价为3元的小工艺品，但如果他们各自为要买的文具付款后，只有小贤还剩2元钱．他们要怎样做才能既买到各自的文具，又都买到小工艺品，请通过运算说明．
【分析】
（1）设笔记本的单价为x元，单独购买一支笔芯的价格为y元，根据“小贤要买3支笔芯，2本笔记本需花费19元；小艺要买7支笔芯，1本笔记本需花费26元”，即可得出关于x，y的二元一次方程组，解之即可得出结论；
（2）先求两人带的总钱数，再求出两人合在一起买文具所需费用，由二者的差大于2个小工艺品所需钱数，可找出：他们合在一起购买，才能既买到各自的文具，又都买到小工艺品．
【解析】
（1）设笔记本的单价为x元，单独购买一支笔芯的价格为y元，
依题意，得：2x+3y=19x+7y=26，
解得：x=5y=3．
答：笔记本的单价为5元，单独购买一支笔芯的价格为3元．
（2）小贤和小艺带的总钱数为19+2+26＝47（元）．
两人合在一起购买所需费用为5×（2+1）+（3﹣0.5）×10＝40（元）．
∵47﹣40＝7（元），3×2＝6（元），7＞6，
∴他们合在一起购买，才能既买到各自的文具，又都买到小工艺品．
6.（2020•重庆）“中国人的饭碗必须牢牢掌握在咱们自己手中”．为优选品种，提高产量，某农业科技小组对A，B两个小麦品种进行种植对比实验研究．去年A，B两个品种各种植了10亩．收获后A，B两个品种的售价均为2.4元/kg，且B的平均亩产量比A的平均亩产量高100kg，A，B两个品种全部售出后总收入为21600元．
（1）请求出A，B两个品种去年平均亩产量分别是多少？
（2）今年，科技小组加大了小麦种植的科研力度，在A，B种植亩数不变的情况下，预计A，B两个品种平均亩产量将在去年的基础上分别增加a%和2a%．由于B品种深受市场的欢迎，预计每千克价格将在去年的基础上上涨a%，而A品种的售价不变．A，B两个品种全部售出后总收入将在去年的基础上增加209a%．求a的值．
【分析】
（1）设A、B两个品种去年平均亩产量分别是x千克和y千克；根据题意列方程组即可得到结论；
（2）根据题意列方程即可得到结论．
【解析】
（1）设A、B两个品种去年平均亩产量分别是x千克和y千克；
根据题意得，y−x=10010×2.4(x+y)=21600，
解得：x=400y=500，
答：A、B两个品种去年平均亩产量分别是400千克和500千克；
（2）2.4×400×10（1+a%）+2.4（1+a%）×500×10（1+2a%）＝21600（1+209a%），
解得：a＝10，
答：a的值为10．
考点02不等式的应用
3、列不等式（组）解决实际问题
列不等式（组）解应用题的基本步骤如下：
①审题；②设未知数；③列不等式(组)；④解不等式(组)；⑤检验并写出答案．
考情总结：列不等式（组）解决实际问题常与一元一次方程、一次函数等综合考查，涉及的题型常与方案设计型问题相联系，如最大利润、最优方案等．列不等式时，要抓住关键词，如不大于、不超过、至多用“≤”连接，不少于、不低于、至少用“≥”连接．
1.（2022·四川泸州）某经销商计划购进，两种农产品．已知购进种农产品2件，种农产品3件，共需690元；购进种农产品1件，种农产品4件，共需720元．
(1)，两种农产品每件的价格分别是多少元？(2)该经销商计划用不超过5400元购进，两种农产品共40件，且种农产品的件数不超过B种农产品件数的3倍．如果该经销商将购进的农产品按照种每件160元，种每件200元的价格全部售出，那么购进，两种农产品各多少件时获利最多？
【答案】(1)A每件进价120元，B每件进价150元；
(2)A农产品进20件，B农产品进20件，最大利润是1800元．
【分析】（1）根据“购进种农产品2件，种农产品3件，共需690元；购进种农产品1件，种农产品4件，共需720元”可以列出相应的方程组，从而可以求得A、B两种农产品每件的价格分别是多少元；（2）根据题意可以得到利润与购买甲种商品的函数关系式，从而可以解答本题．
【解析】 (1)设A每件进价x元，B每件进价y元，
由题意得，解得：，
答：A每件进价120元，B每件进价150元；
(2)设A农产品进a件，B农产品（40-a）件，由题意得，
解得，
设利润为y元，则，
∵y随a的增大而减小，
∴当a=20时，y最大， 最大值y=2000-10×200=1800，
答：A农产品进20件，B农产品进20件，最大利润是1800元．
【点睛】本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式的应用，解答本题的关键是明确题意，利用一次函数的性质和不等式的性质解答．
2．（2021·四川成都市·中考真题）为改善城市人居环境，《成都市生活垃圾管理条例》（以下简称《条例》）于2021年3月1日起正式施行．某区域原来每天需要处理生活垃圾920吨，刚好被12个A型和10个B型预处置点位进行初筛、压缩等处理．已知一个A型点位比一个B型点位每天多处理7吨生活垃圾．
（1）求每个B型点位每天处理生活垃圾的吨数；
（2）由于《条例》的施行，垃圾分类要求提高，现在每个点位每天将少处理8吨生活垃圾，同时由于市民环保意识增强，该区域每天需要处理的生活垃圾比原来少10吨．若该区域计划增设A型、B型点位共5个，试问至少需要增设几个A型点位才能当日处理完所有生活垃圾？
【答案】（1）38吨；（2）3个
【分析】
（1）设每个B型点位每天处理生活垃圾的吨数为x，则A型为x+7，由每天需要处理生活垃圾920吨列出方程求解即可；
（2）设至少需要增设y个A型点位才能当日处理完所有生活垃圾．则B型为5-y，根据两种需要处理的生活垃圾和不低于910吨列不等式求解即可．
【详解】
解：（1）设每个B型点位每天处理生活垃圾的吨数为x，则A型为x+7，
由题意得：10x+12（x+7）=920，
解得：x=38，
答：每个B型点位每天处理生活垃圾为38吨数；
（2）设至少需要增设y个A型点位才能当日处理完所有生活垃圾．则B型为5-y．
由题意得（12+y）(38+7-8)+（10+5-y）（38-8）≥920-10
解得：y≥ ，
∵y为整数
∴至少需要增设3个A型点位，
答：至少需要增设3个A型点位才能当日处理完所有生活垃圾．
【点睛】
本题考查一元一次方程以及一元一次不等式的应用，将现实生活中的事件与数学思想联系起来，读懂题列出关系式是解题关键．
3．（2021·四川眉山市·中考真题）为进一步落实“德、智、体、美、劳”五育并举工作，某中学以体育为突破口，准备从体育用品商场一次性购买若千个足球和篮球，用于学校球类比赛活动．每个足球的价格都相同，每个篮球的价格也相同．已知篮球的单价比足球单价的2倍少30元，用1200元购买足球的数量是用900元购买篮球数量的2倍．
（1）足球和篮球的单价各是多少元？
（2）根据学校实际情况，需一次性购买足球和篮球共200个，但要求足球和篮球的总费用不超过15500元，学校最多可以购买多少个篮球？
【答案】（1）每个足球60元，每个篮球90元；（2）最多购进篮球116个
【分析】
（1）设一个足球的单价x元，已知篮球的单价比足球单价的2倍少30元，则一个篮球的单价为（2x-30）元，根据“用1200元购买足球的数量是用900元购买篮球数量的2倍”列方程求解即可；
（2）设买篮球m个，则买足球（200-m）个，根据购买足球和篮球的总费用不超过15500元建立不等式求出解即可．
【详解】
解：（1）设每个足球x元，每个篮球（2x-30）元，
根据题意得：，
解得x=60，
经检验x=60是方程的根且符合题意，
2x-30=90，
答：每个足球60元，每个篮球90元．
（2）设设买篮球m个，则买足球（200-m）个，
由题意得：，
解得．
∵ m为正整数，∴ 最多购进篮球116个．
【点睛】
本题考查了列一元一次方程解实际问题的运用，列一元一次不等式解实际问题的运用，解答本题时找到方程的等量关系和建立不等式的不等关系是解答本题的关键．
4.（2021·浙江温州市·中考真题）某公司生产的一种营养品信息如下表．已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克．
（1）问甲、乙两种食材每千克进价分别是多少元？
（2）该公司每日用18000元购进甲、乙两种食材并恰好全部用完．
①问每日购进甲、乙两种食材各多少千克？
②已知每日其他费用为2000元，且生产的营养品当日全部售出．若A的数量不低于B的数量，则A为多少包时，每日所获总利润最大？最大总利润为多少元？
【答案】（1）甲、乙两种食材每千克进价分别为40元、20元；（2）①每日购进甲食材400千克，乙食材100千克；②当为400包时，总利润最大．最大总利润为2800元
【分析】
（1）设乙食材每千克进价为元，根据用80元购买的甲食材比用20元购买的乙食材多1千克列分式方程即可求解；
（2）①设每日购进甲食材千克，乙食材千克．根据每日用18000元购进甲、乙两种食材并恰好全部用完，利用进货总金额为180000元，含铁量一定列出二元一次方程组即可求解；
②设为包，根据题意，可以得到每日所获总利润与m的函数关系式，再根据A的数量不低于B的数量，可以得到m的取值范围，从而可以求得总利润的最大值．
【详解】
解：（1）设乙食材每千克进价为元，则甲食材每千克进价为元，
由题意得，解得．
经检验，是所列方程的根，且符合题意．
（元）．
答：甲、乙两种食材每千克进价分别为40元、20元．
（2）①设每日购进甲食材千克，乙食材千克．
由题意得，解得
答：每日购进甲食材400千克，乙食材100千克．
②设为包，则为包．
记总利润为元，则
．
的数量不低于的数量，
，．
，随的增大而减小。
当时，的最大值为2800元．
答：当为400包时，总利润最大．最大总利润为2800元．
【点睛】
本题主要考查了一次函数的应用、分式方程、二元一次方程的应用，解答本题时要明确题意、弄清表格数据的意义及各种量之间关系，利用方程的求未知量和一次函数的性质解答，注意分式方程要检验．
5.（2021·四川资阳市·中考真题）我市某中学计划举行以“奋斗百年路，启航新征程”为主题的知识竞赛，并对获奖的同学给予奖励．现要购买甲、乙两种奖品，已知1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元．
（1）求甲、乙两种奖品的单价；
（2）根据颁奖计划，该中学需甲、乙两种奖品共60件，且甲种奖品的数量不少于乙种奖品数量的，应如何购买才能使总费用最少？并求出最少费用．
【答案】（1）甲种奖品的单价为20元，乙种奖品的单价为10元；（2）购买甲种奖品20件，乙种奖品40件时总费用最少，最少费用为800元．
【分析】
（1）设甲种奖品的单价为x元，乙种奖品的单价为y元，根据题意列方程组求出x、y的值即可得答案；
（2）设总费用为w元，购买甲种奖品为m件，根据甲种奖品的数量不少于乙种奖品数量的可得m的取值范围，根据需甲、乙两种奖品共60件可得购买乙种奖品为（60-m）件，根据（1）中所求单价可得w与m的关系式，根据一次函数的性质即可得答案．
【详解】
（1）设甲种奖品的单价为x元，乙种奖品的单价为y元，
∵1件甲种奖品和2件乙种奖品共需40元，2件甲种奖品和3件乙种奖品共需70元，
∴，
解得：，
答：甲种奖品的单价为20元，乙种奖品的单价为10元．
（2）设总费用为w元，购买甲种奖品为m件，
∵需甲、乙两种奖品共60件，
∴购买乙种奖品为（60-m）件，
∵甲种奖品的单价为20元，乙种奖品的单价为10元，
∴w=20m+10（60-m）=10m+600，
∵甲种奖品的数量不少于乙种奖品数量的，
∴m≥（60-m），
∴20≤m≤60，
∵10>0，
∴w随m的增大而增大，
∴当m=20时，w有最小值，最小值为10×20+600=800（元），
∴购买甲种奖品20件，乙种奖品40件时总费用最少，最少费用为800元．
【点睛】
本题考查二元一次方程组的应用、一元一次不等式的应用及一次函数的应用，正确得出等量关系及不等关系列出方程组及不等式，熟练掌握一次函数的性质是解题关键．
6.（2021·江苏连云港市·中考真题）为了做好防疫工作，学校准备购进一批消毒液．已知2瓶A型消毒液和3瓶B型消毒液共需41元，5瓶A型消毒液和2瓶B型消毒液共需53元．
（1）这两种消毒液的单价各是多少元？
（2）学校准备购进这两种消毒液共90瓶，且B型消毒液的数量不少于A型消毒液数量的，请设计出最省钱的购买方案，并求出最少费用．
【答案】（1）种消毒液的单价是7元，型消毒液的单价是9元；（2）购进种消毒液67瓶，购进种23瓶，最少费用为676元
【分析】
（1）根据题中条件列出二元一次方程组，求解即可；
（2）利用由（1）求出的两种消毒液的单价，表示出购买的费用的表达式，根据购买两种消毒液瓶数之间的关系，求出引进表示瓶数的未知量的范围，即可确定方案．
【详解】
解：（1）设种消毒液的单价是元，型消毒液的单价是元．
由题意得：，解之得，，
答：种消毒液的单价是7元，型消毒液的单价是9元．
（2）设购进种消毒液瓶，则购进种瓶，购买费用为元．
则，
∴随着的增大而减小，最大时，有最小值．
又，∴．
由于是整数，最大值为67，
即当时，最省钱，最少费用为元．
此时，．
最省钱的购买方案是购进种消毒液67瓶，购进种23瓶．
【点睛】
本题考查了二元一次不等式组的求解及利用一次函数的增减性来解决生活中的优化决策问题，解题的关键是：仔细审题，找到题中的等量关系，建立等式进行求解．
考点03分式方程的应用
4．分式方程的应用
（1）分式方程的应用主要涉及工程问题，有工作量问题、行程问题等．
每个问题中涉及到三个量的关系，如：工作时间＝，时间＝等．
（2）列分式方程解应用题的一般步骤：
①设未知数；
②找等量关系；
③列分式方程；
④解分式方程；
⑤检验（一验分式方程，二验实际问题）；
⑥答．
1.（2022·重庆）在全民健身运动中，骑行运动颇受市民青睐，甲、乙两骑行爱好者约定从地沿相同路线骑行去距地30千米的地，已知甲骑行的速度是乙的1.2倍．
(1)若乙先骑行2千米，甲才开始从地出发，则甲出发半小时恰好追上乙，求甲骑行的速度；
(2)若乙先骑行20分钟，甲才开始从地出发，则甲、乙恰好同时到达地，求甲骑行的速度．
【答案】(1) (2)千米/时
【分析】（1）设乙的速度为千米/时，则甲的速度为千米/时，根据甲出发半小时恰好追上乙列方程求解即可；（2）设乙的速度为千米/时，则甲的速度为千米/时，根据甲、乙恰好同时到达地列方程求解即可．
(1)解：设乙的速度为千米/时，则甲的速度为千米/时，
由题意得：，解得：，
则（千米/时），
答：甲骑行的速度为千米/时；
(2)设乙的速度为千米/时，则甲的速度为千米/时，
由题意得：，解得，
经检验是分式方程的解，
则（千米/时），
答：甲骑行的速度为千米/时．
【点睛】本题考查了一元一次方程的应用和分式方程的应用，找准等量关系，正确列出方程是解题的关键．
2.（2020•泰州）近年来，我市大力发展城市快速交通，小王开车从家到单位有两条路线可选择，路线A为全程25km的普通道路，路线B包含快速通道，全程30km，走路线B比走路线A平均速度提高50%，时间节省6min，求走路线B的平均速度．
【分析】设走路线A的平均速度为xkm/h，则走路线B的平均速度为（1+50%）xkm/h，根据时间＝路程÷速度结合走路线B比走路线A少用6min，即可得出关于x的分式方程，解之经检验后即可得出结论．
【解析】设走路线A的平均速度为xkm/h，则走路线B的平均速度为（1+50%）xkm/h，
依题意，得：25x−30(1+50%)x=660，
解得：x＝50，
经检验，x＝50是原方程的解，且符合题意，
∴（1+50%）x＝75．
答：走路线B的平均速度为75km/h．
3.（2020•常德）第5代移动通信技术简称5G，某地已开通5G业务，经测试5G下载速度是4G下载速度的15倍，小明和小强分别用5G与4G下载一部600兆的公益片，小明比小强所用的时间快140秒，求该地4G与5G的下载速度分别是每秒多少兆？
【分析】首先设该地4G的下载速度是每秒x兆，则该地5G的下载速度是每秒15x兆，根据题意可得等量关系：4G下载600兆所用时间﹣5G下载600兆所用时间＝140秒．然后根据等量关系，列出分式方程，再解即可．
【解析】设该地4G的下载速度是每秒x兆，则该地5G的下载速度是每秒15x兆，
由题意得：600x−60015x=140，
解得：x＝4，
经检验：x＝4是原分式方程的解，且符合题意，
15×4＝60，
答：该地4G的下载速度是每秒4兆，则该地5G的下载速度是每秒60兆．
4.（2020•广东）某社区拟建A，B两类摊位以搞活“地摊经济”，每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米．建A类摊位每平方米的费用为40元，建B类摊位每平方米的费用为30元．用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的35．
（1）求每个A，B类摊位占地面积各为多少平方米？
（2）该社区拟建A，B两类摊位共90个，且B类摊位的数量不少于A类摊位数量的3倍．求建造这90个摊位的最大费用．
【分析】
（1）设每个B类摊位的占地面积为x平方米，则每个A类摊位占地面积为（x+2）平方米，根据用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的35这个等量关系列出方程即可．
（2）设建A摊位a个，则建B摊位（90﹣a）个，结合“B类摊位的数量不少于A类摊位数量的3倍”列出不等式并解答．
【解析】
（1）设每个B类摊位的占地面积为x平方米，则每个A类摊位占地面积为（x+2）平方米，
根据题意得：60x+2=60x⋅35，
解得：x＝3，
经检验x＝3是原方程的解，
所以3+2＝5，
答：每个A类摊位占地面积为5平方米，每个B类摊位的占地面积为3平方米；
（2）设建A摊位a个，则建B摊位（90﹣a）个，
由题意得：90﹣a≥3a，
解得a≤22.5，
∵建A类摊位每平方米的费用为40元，建B类摊位每平方米的费用为30元，
∴要想使建造这90个摊位有最大费用，所以要多建造A类摊位，即a取最大值22时，费用最大，
此时最大费用为：22×40×5+30×（90﹣22）×3＝10520，
答：建造这90个摊位的最大费用是10520元．
5.（2021·山东聊城市·中考真题）为迎接建党一百周年，我市计划用两种花卉对某广场进行美化．已知用600元购买A种花卉与用900元购买B种花卉的数量相等，且B种花卉每盆比A种花卉多0.5元．
（1）A，B两种花卉每盆各多少元？
（2）计划购买A，B两种花卉共6000盆，其中A种花卉的数量不超过B种花卉数量的，求购买A种花卉多少盆时，购买这批花卉总费用最低，最低费用是多少元？
【答案】（1）A 种花弃每盆1元，B种花卉每盆1.5元；（2）购买A 种花卉1500盆时购买这批花卉总费用最低，最低费用为 8250元
【分析】
（1）设A 种花弃每盆x元，B 种花卉每盆（x＋0.5）元，根据题意列分式方程，解出方程并检验；
（2）设购买A种花卉∶t盆，购买这批花卉的总费用为w元，则t≤（6000－t），w＝t＋1.5（6000－t）＝－0.5t＋9000，w随t的增大而减小，所以根据t的范围可以求得w的最小值．
【详解】
解：（1）设A 种花弃每盆x元，B 种花卉每盆（x＋0.5）元．
根据题意，得．
解这个方程，得x＝1.
经检验知，x＝1是原分式方程的根，并符合题意．
此时x＋0.5＝1＋0.5＝1.5（元）．
所以，A种花弃每盆1元，B种花卉每盆1.5元．
（2）设购买A种花卉∶t盆，购买这批花卉的总费用为w元，则t≤（6000－t），
解得∶t≤1500.
由题意，得w＝t＋1.5（6000－t）＝－0.5t＋9000.
因为w是t的一次函数，k＝－0.5＜0，w随t的增大而减小，所以当t＝1500 盆时，w最小．
w＝－0.5×1500＋9000＝8250（元）．
所以，购买A种花卉1500盆时购买这批花卉总费用最低，最低费用为8250元．
【点睛】
本题主要考查了分式方程解决实际问题和一次函数求最值，根据等量关系列出方程和函数关系式及取值范围是解题关键．
6.（2021·湖南中考真题）“七一”建党节前夕，某校决定购买，两种奖品，用于表彰在“童心向党”活动中表现突出的学生．已知奖品比奖品每件多25元预算资金为1700元，其中800元购买奖品，其余资金购买奖品，且购买奖品的数量是奖品的3倍．
（1）求，奖品的单价；
（2）购买当日，正逢该店搞促销活动，所有商品均按原价八折销售，学校调整了购买方案：不超过预算资金且购买奖品的资金不少于720元，，两种奖品共100件．求购买，两种奖品的数量，有哪几种方案？
【答案】（1）A，奖品的单价分别是40元，15元；（2）购买A奖品23件，B奖品77件；购买A奖品24件，B奖品76件；购买A奖品25件，B奖品75件．
【分析】
（1）设B奖品的单价为x元，则A奖品的单价为(x+25)元，根据“购买奖品的数量是奖品的3倍”，列出分式方程，即可求解；
（2）设购买A奖品a件，则购买B奖品(100-a)件，列出一元一次不等式组，即可求解．
【详解】
（1）解：设B奖品的单价为x元，则A奖品的单价为(x+25)元，
由题意得：，解得：x=15，
经检验：x=15是方程的解，且符合题意，
15+25=40，
答：A，奖品的单价分别是40元，15元；
（2）设购买A奖品a件，则购买B奖品(100-a)件，
由题意得：，解得：22.5≤a≤25，
∵a取正整数，
∴a=23，24，25，
答：购买A奖品23件，B奖品77件；购买A奖品24件，B奖品76件；购买A奖品25件，B奖品75件．
【点睛】
本题主要考查分式方程以及一元一次不等式组的实际应用，找准数量关系，列出方程和不等式组，是解题的关键．
7.（2020•牡丹江）某商场准备购进A，B两种书包，每个A种书包比B种书包的进价少20元，用700元购进A种书包的个数是用450元购进B种书包个数的2倍，A种书包每个标价是90元，B种书包每个标价是130元．请解答下列问题：
（1）A，B两种书包每个进价各是多少元？
（2）若该商场购进B种书包的个数比A种书包的2倍还多5个，且A种书包不少于18个，购进A，B两种书包的总费用不超过5450元，则该商场有哪几种进货方案？
（3）该商场按（2）中获利最大的方案购进书包，在销售前，拿出5个书包赠送给某希望小学，剩余的书包全部售出，其中两种书包共有4个样品，每种样品都打五折，商场仍获利1370元．请直接写出赠送的书包和样品中，B种书包各有几个？
【分析】
（1）设每个A种书包的进价为x元，则每个B种书包的进价为（x+20）元，根据数量＝总价÷单价结合用700元购进A种书包的个数是用450元购进B种书包个数的2倍，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）设该商场购进m个A种书包，则购进（2m+5）个B种书包，根据购进A，B两种书包的总费用不超过5450元且A种书包不少于18个，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为正整数即可得出各进货方案；
（3）设销售利润为w元，根据总利润＝销售每个书包的利润×销售数量，即可得出w关于m的函数关系式，利用一次函数的性质可得出获得利润最大的进货方案，设赠送的书包中B种书包有a个，样品中B种书包有b个，则赠送的书包中A种书包有（5﹣a）个，样品中A种书包有（4﹣b）个，根据利润＝销售收入﹣成本，即可得出关于a，b的二元一次方程，结合a，b，（5﹣a），（4﹣b）均为正整数，即可求出结论．
【解析】
（1）设每个A种书包的进价为x元，则每个B种书包的进价为（x+20）元，
依题意，得：700x=2×450x+20，
解得：x＝70，
经检验，x＝70是原方程的解，且符合题意，
∴x+20＝90．
答：每个A种书包的进价为70元，每个B种书包的进价为90元．
（2）设该商场购进m个A种书包，则购进（2m+5）个B种书包，
依题意，得：m≥1870m+90(2m+5)≤5450，
解得：18≤m≤20．
又∵m为正整数，
∴m可以为18，19，20，
∴该商场有3种进货方案，方案1：购买18个A种书包，41个B种书包；方案2：购买19个A种书包，43个B种书包；方案3：购买20个A种书包，45个B种书包．
（3）设销售利润为w元，则w＝（90﹣70）m+（130﹣90）（2m+5）＝100m+200．
∵k＝100＞0，
∴w随m的增大而增大，
∴当m＝20时，w取得最大值，此时2m+5＝45．
设赠送的书包中B种书包有a个，样品中B种书包有b个，则赠送的书包中A种书包有（5﹣a）个，样品中A种书包有（4﹣b）个，
依题意，得：90×[20﹣（5﹣a）﹣（4﹣b）]+0.5×90（4﹣b）+130（45﹣a﹣b）+0.5×130b﹣70×20﹣90×45＝1370，
∴b＝10﹣2a．
∵a，b，（5﹣a），（4﹣b）均为正整数，
∴a=4b=2．
答：赠送的书包中B种书包有4个，样品中B种书包有2个．
8.（2020•黔西南州）随着人们“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行，也给自行车商家带来商机．某自行车行经营的A型自行车去年销售总额为8万元．今年该型自行车每辆售价预计比去年降低200元．若该型车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求：
（1）A型自行车去年每辆售价多少元？
（2）该车行今年计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍．已知A型车和B型车的进货价格分别为1500元和1800元，计划B型车销售价格为2400元，应如何组织进货才能使这批自行车销售获利最多？
【分析】
（1）设去年A型车每辆售价x元，则今年售价每辆为（x﹣200）元，由卖出的数量相同建立方程求出其解即可；
（2）设今年新进A型车a辆，则B型车（60﹣a）辆，获利y元，由条件表示出y与a之间的关系式，由a的取值范围就可以求出y的最大值．
【解析】
（1）设去年A型车每辆售价x元，则今年售价每辆为（x﹣200）元，由题意，得
80000x=80000(1−10%)x−200，
解得：x＝2000．
经检验，x＝2000是原方程的根．
答：去年A型车每辆售价为2000元；
（2）设今年新进A型车a辆，则B型车（60﹣a）辆，获利y元，由题意，得
y＝（1800﹣1500）a+（2400﹣1800）（60﹣a），
y＝﹣300a+36000．
∵B型车的进货数量不超过A型车数量的两倍，
∴60﹣a≤2a，
∴a≥20．
∵y＝﹣300a+36000．
∴k＝﹣300＜0，
∴y随a的增大而减小．
∴a＝20时，y有最大值
∴B型车的数量为：60﹣20＝40辆．
∴当新进A型车20辆，B型车40辆时，这批车获利最大
考点04二次方程的应用
5、利用一元二次方程解决实际问题
列一元二次方程解应用题步骤和列一元一次方程(组)解应用题步骤一样，即审、设、列、解、验、答六步．列一元二次方程解应用题，经济类和面积类问题是常考内容．
6．增长率等量关系
（1）增长率=增长量÷基础量．
（2）设为原来量，为平均增长率，为增长次数，为增长后的量，则；当为平均下降率时，则有．
7．利润等量关系
（1）利润=售价－成本．
（2）利润率=×100％．
8．面积问题
（1）类型1：如图1所示的矩形长为，宽为，空白“回形”道路的宽为，则阴影部分的面积为．
（2）类型2：如图2所示的矩形长为，宽为，阴影道路的宽为，则空白部分的面积为．
（3）类型3：如图3所示的矩形长为，宽为，阴影道路的宽为，则4块空白部分的面积之和可转化为．

1.（2022·四川眉山）建设美丽城市，改造老旧小区．某市2019年投入资金1000万元，2021年投入资金1440万元，现假定每年投入资金的增长率相同．
(1)求该市改造老旧小区投入资金的年平均增长率；
(2)2021年老旧小区改造的平均费用为每个80万元．2022年为提高老旧小区品质，每个小区改造费用增加15%．如果投入资金年增长率保持不变，求该市在2022年最多可以改造多少个老旧小区？
【答案】(1)20% (2)18个
【分析】（1）先设该市改造老旧小区投入资金的年平均增长率为，根据2019年投入资金2021年投入的总资金，列出方程求解即可；
（2）由（1）得出的资金年增长率求出2022年的投入资金，然后2022年改造老旧小区的总费用要小于等于2022年投入资金，列出不等式求解即可．
【解析】(1)解：设该市改造老旧小区投入资金的年平均增长率为，
根据题意得：，解这个方程得，，，
经检验，符合本题要求．
答：该市改造老旧小区投入资金的年平均增长率为20%．
(2)设该市在2022年可以改造个老旧小区，
由题意得：，解得．
∵为正整数，∴最多可以改造18个小区．
答：该市在2022年最多可以改造18个老旧小区．
【点睛】此题考查了一元二次方程的应用，不等式的应用，解决此题的关键是找到相应的等量关系和相应的不等关系，列出正确的方程和不等式．
2.（2022·湖北宜昌）某造纸厂为节约木材，实现企业绿色低碳发展，通过技术改造升级，使再生纸项目的生产规模不断扩大．该厂3，4月份共生产再生纸800吨，其中4月份再生纸产量是3月份的2倍少100吨．(1)求4月份再生纸的产量；(2)若4月份每吨再生纸的利润为1000元，5月份再生纸产量比上月增加．5月份每吨再生纸的利润比上月增加，则5月份再生纸项目月利润达到66万元．求的值；(3)若4月份每吨再生纸的利润为1200元，4至6月每吨再生纸利润的月平均增长率与6月份再生纸产量比上月增长的百分数相同，6月份再生纸项目月利润比上月增加了．求6月份每吨再生纸的利润是多少元？
【答案】(1)4月份再生纸的产量为500吨(2)的值20(3)6月份每吨再生纸的利润是1500元
【分析】（1）设3月份再生纸产量为吨，则4月份的再生纸产量为吨，然后根据该厂3，4月份共生产再生纸800吨，列出方程求解即可；
（2）根据总利润=每一吨再生纸的利润×数量列出方程求解即可；
（3）设4至6月每吨再生纸利润的月平均增长率为，5月份再生纸的产量为吨，根据总利润=每一吨再生纸的利润×数量列出方程求解即可；
【解析】(1)解：设3月份再生纸产量为吨，则4月份的再生纸产量为吨，
由题意得：，解得：，∴，
答：4月份再生纸的产量为500吨；
(2)解：由题意得：，
解得：或（不合题意，舍去）
∴，∴的值20；
(3)解：设4至6月每吨再生纸利润的月平均增长率为，5月份再生纸的产量为吨，
∴
答：6月份每吨再生纸的利润是1500元．
【点睛】本题主要考查了一元一次方程的应用，一元二次方程的应用，正确理解题意，列出方程求解是解题的关键．
3.（2021·四川遂宁市·中考真题）某服装店以每件30元的价格购进一批T恤，如果以每件40元出售，那么一个月内能售出300件，根据以往销售经验，销售单价每提高1元，销售量就会减少10件，设T恤的销售单价提高元．
（1）服装店希望一个月内销售该种T恤能获得利润3360元，并且尽可能减少库存，问T恤的销售单价应提高多少元？
（2）当销售单价定为多少元时，该服装店一个月内销售这种T恤获得的利润最大？最大利润是多少元？
【答案】（1）2元；（2）当服装店将销售单价50元时，得到最大利润是4000元
【分析】
（1）根据题意，通过列一元二次方程并求解，即可得到答案；
（2）设利润为M元，结合题意，根据二次函数的性质，计算得利润最大值对应的的值，从而得到答案．
【详解】
（1）由题意列方程得：（x＋40-30） （300-10x）＝3360
解得：x1＝2，x2＝18
∵要尽可能减少库存，
∴x2＝18不合题意，故舍去
∴T恤的销售单价应提高2元；
（2）设利润为M元，由题意可得：
M＝（x＋40-30）（300-10x）＝-10x2＋200x＋3000＝
∴当x＝10时，M最大值＝4000元
∴销售单价：40＋10＝50元
∴当服装店将销售单价50元时，得到最大利润是4000元．
【点睛】
本题考查了一元二次方程、二次函数的知识；解题的关键是熟练掌握一元二次方程、二次函数的性质，从而完成求解．
4.（2021·重庆中考真题）重庆小面是重庆美食的名片之一，深受外地游客和本地民众欢迎．某面馆向食客推出经典特色重庆小面，顾客可到店食用（简称“堂食”小面），也可购买搭配佐料的袋装生面（简称“生食”小面）．已知3份“堂食”小面和2份“生食”小面的总售价为31元，4份“堂食”小面和1份“生食”小面的总售价为33元．
（1）求每份“堂食”小面和“生食”小面的价格分别是多少元？
（2）该面馆在4月共卖出“堂食”小面4500份，“生食”小面2500份，为回馈广大食客，该面馆从5月1日起每份“堂食”小面的价格保持不变，每份“生食”小面的价格降低．统计5月的销量和销售额发现：“堂食”小面的销量与4月相同，“生食”小面的销量在4月的基础上增加，这两种小面的总销售额在4月的基础上增加．求a的值．
【答案】（1）每份“堂食”小面价格是7元，“生食”小面的价格是5元．（2）a的值为8．
【分析】
（1）设每份“堂食”小面和“生食”小面的价格分别是x、y元，根据题意列出二元一次方程组，解方程组即可；
（2）根据题意列出一元二次方程，解方程即可．
【详解】
解：（1）设每份“堂食”小面和“生食”小面的价格分别是x、y元，根据题意列方程组得，，
解得，，
答：每份“堂食”小面价格是7元，“生食”小面的价格是5元．
（2）根据题意得，，
解得，（舍去），，
答：a的值为8．
【点睛】
本题考查了二元一次方程组的应用和一元二次方程的应用，解题关键是找准题目中的等量关系，列出方程，熟练运用相关知识解方程．
5.（2021·重庆中考真题）某工厂有甲、乙两个车间，甲车间生产A产品，乙车间生产B产品，去年两个车间生产产品的数量相同且全部售出．已知A产品的销售单价比B产品的销售单价高100元，1件A产品与1件B产品售价和为500元．
（1）A、B两种产品的销售单价分别是多少元？
（2）随着5G时代的到来，工业互联网进入了快速发展时期．今年，该工厂计划依托工业互联网将乙车间改造为专供用户定制B产品的生产车间．预计A产品在售价不变的情况下产量将在去年的基础上增加a%；B产品产量将在去年的基础上减少a%，但B产品的销售单价将提高3a%．则今年A、B两种产品全部售出后总销售额将在去年的基础上增加%．求a的值．
【答案】（1）A产品的销售单价为300元，B产品的销售单价为200元；（2）20
【分析】
（1）设B产品的销售单价为x元，则A产品的销售单价为（x+100）元，根据题意列出方程解出即可；
（2）设去年每个车间生产产品的数量为t件，根据题意根据题意列出方程解出即可；
【详解】
解：（1）设B产品的销售单价为x元，则A产品的销售单价为（x+100）元．
根据题意，得
．
解这个方程，得．
则．
答：A产品的销售单价为300元，B产品的销售单价为200元．
（2）设去年每个车间生产产品的数量为t件，根据题意，得
设a%=m，则原方程可化简为．
解这个方程，得（舍去）．
∴a=20．
答：a的值是20．
【点睛】
本题考查了一元一次方程的应用以及一元二次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元一次方程；（2）根据各数量之间的关系，正确列出一元二次方程．
时间
销售总额（元）
线上销售额（元）
线下销售额（元）
2019年4月份
a
x
a﹣x
2020年4月份
1.1a
1.43x
1.04（a﹣x）
营养品信息表
营养成份
每千克含铁42毫克
配料表
原料
每千克含铁
甲食材
50毫克
乙食材
10毫克
规格
每包食材含量
每包单价
A包装
1千克
45元
B包装
0.25千克
12元