高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体优秀随堂练习题

这是一份高中数学人教A版 (2019)必修 第二册9.2 用样本估计总体优秀随堂练习题，共20页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。

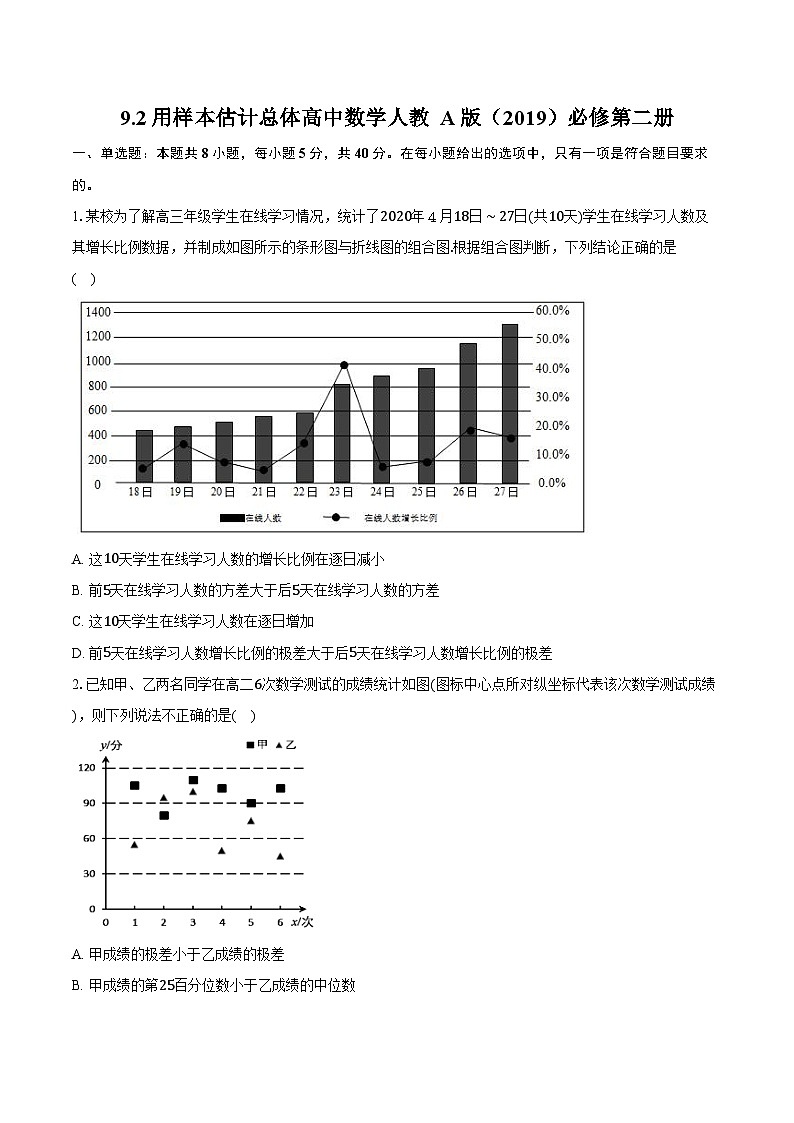
1.某校为了解高三年级学生在线学习情况，统计了2020年４月18日∼27日(共10天)学生在线学习人数及其增长比例数据，并制成如图所示的条形图与折线图的组合图.根据组合图判断，下列结论正确的是
( )
A. 这10天学生在线学习人数的增长比例在逐日减小
B. 前5天在线学习人数的方差大于后5天在线学习人数的方差
C. 这10天学生在线学习人数在逐日增加
D. 前5天在线学习人数增长比例的极差大于后5天在线学习人数增长比例的极差
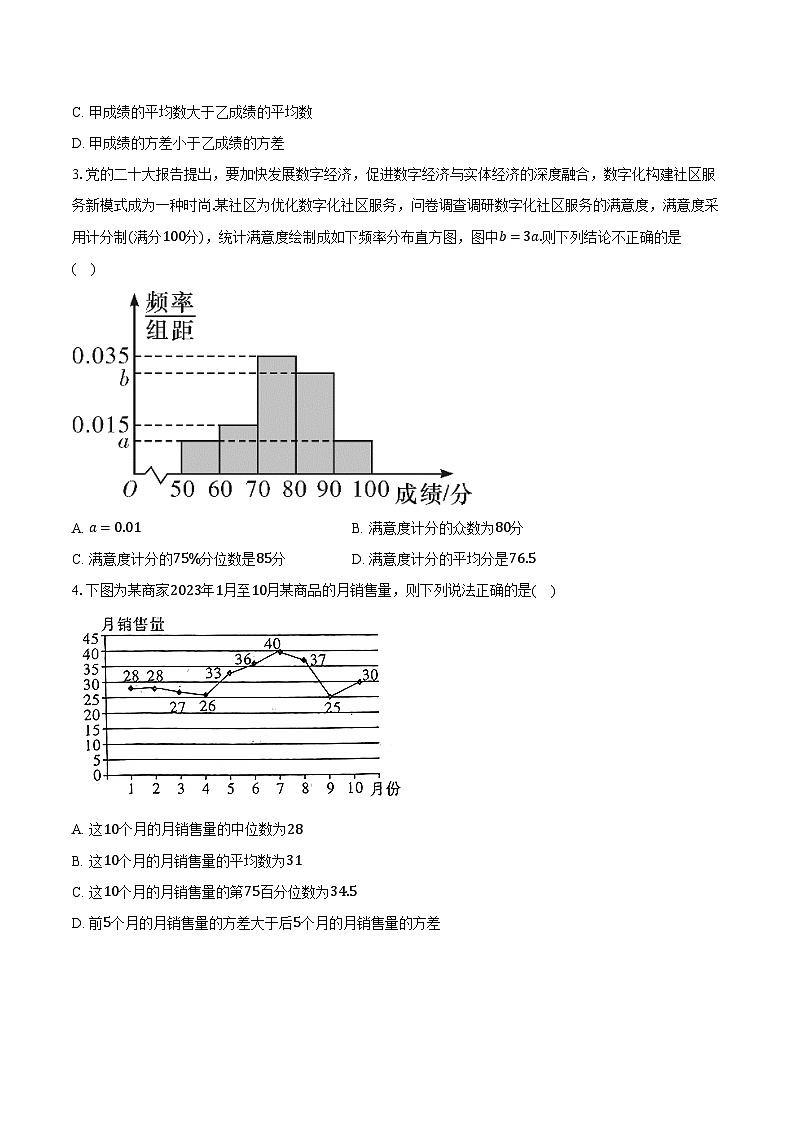
2.已知甲、乙两名同学在高二6次数学测试的成绩统计如图(图标中心点所对纵坐标代表该次数学测试成绩)，则下列说法不正确的是( )
A. 甲成绩的极差小于乙成绩的极差
B. 甲成绩的第25百分位数小于乙成绩的中位数
C. 甲成绩的平均数大于乙成绩的平均数
D. 甲成绩的方差小于乙成绩的方差
3.党的二十大报告提出，要加快发展数字经济，促进数字经济与实体经济的深度融合，数字化构建社区服务新模式成为一种时尚.某社区为优化数字化社区服务，问卷调查调研数字化社区服务的满意度，满意度采用计分制(满分100分)，统计满意度绘制成如下频率分布直方图，图中b=3a.则下列结论不正确的是
( )
A. a=0.01B. 满意度计分的众数为80分
C. 满意度计分的75%分位数是85分D. 满意度计分的平均分是76.5
4.下图为某商家2023年1月至10月某商品的月销售量，则下列说法正确的是( )
A. 这10个月的月销售量的中位数为28
B. 这10个月的月销售量的平均数为31
C. 这10个月的月销售量的第75百分位数为34.5
D. 前5个月的月销售量的方差大于后5个月的月销售量的方差
5.如图所示的茎叶图记录了甲、乙两支篮球队各6名队员某场比赛的得分数据(单位：分).则下列说法正确的是( )
A. 甲队数据的中位数大于乙队数据的中位数；
B. 甲队数据的平均值小于乙队数据的平均值；
C. 甲队数据的标准差大于乙队数据的标准差；
D. 乙队数据的第75百分位数为27．
6.数据6，4，3，6，3，8，8，3，1，8，则关于这组数据下列说法错误的是( )
A. 中位数为5B. 方差为85C. 平均数为5D. 85%分位数为8
7.为了加深师生对党史的了解，激发广大师生知史爱党､知史爱国的热情，某校举办了“学党史､育文化”暨“喜迎党的二十大”党史知识竞赛，并将1000名师生的竞赛成绩(满分100分，成绩取整数)整理成如图所示的频率分布直方图，则下列说法不正确的是
( )
A. a的值为0.005B. 估计这组数据的众数为75
C. 估计成绩低于60分的有250人D. 估计这组数据的第85百分位数为85
8.每个大学生毕业后都希望找个理想的工作，据中国人民大学中国就业研究所联合智联招聘，发布《2020年大学生就业力报告》可以看出，毕业生更倾向于新经济行业就业，这些行业薪酬待遇优厚、科技含量较高、发展空间较好，下面是毕业生期望行业分布图：
由图可知下列说法正确的个数有
①期望值的极差为24.2%；
②期望值的中位数为6.3%；
③若随机调查100个大学毕业生，则大约有8个毕业生希望从事金融业工作．
A. 0B. 1C. 2D. 3
二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。
9.下图为2022年8月5日通报的14天内31省区市疫情趋势，则下列说法正确的是( )
A. 无症状感染者的极差大于400B. 确诊病例的方差大于无症状感染者的方差
C. 实际新增感染者的平均数小于389D. 实际新增感染者的第80百分位数为641
10.为响应自己城市倡导的低碳出行，小李上班可以选择公交车、自行车两种交通工具，他分别记录了100次坐公交车和骑车所用时间(单位：分钟)，得到下列两个频率分布直方图：基于以上统计信息，则
A. 骑车时间的中位数的估计值是22分钟
B. 坐公交车时间的40%分位数的估计值是19分钟
C. 坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值
D. 坐公交车时间的方差的估计值小于骑车时间的方差的估计值
11.下图是某市6月1日至14日的空气质量指数变化趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，则下列说法正确的是( )
A. 该市14天空气质量指数的平均值大于100
B. 该市14天空气质量指数的中位数为78.5
C. 该市14天空气质量指数的30百分位数为55
D. 计算连续3天空气质量指数的方差，其中6日到8日的方差最大
12.某保险公司为客户定制了5个险种：甲，一年期短险；乙，两全保险；丙，理财类保险；丁，定期寿险；戊，重大疾病保险.各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查，得出如图所示的统计图，以下四个选项中，说法错误的有
( )
A. 54周岁及以上客户人数最少
B. 18∼29周岁客户参保总费用最少
C. 丁险种更受客户青睐
D. 30周岁及以上的客户约占参保客户的80％
三、填空题：本题共4小题，每小题5分，共20分。
13.为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分(十分制)如图所示，假设得分的中位数为m，众数为n，平均数为x，则m，n，x的大小关系为 .(用“<”连接)
14. 为了解中学生课外阅读情况，现从某中学随机抽取200名学生，收集了他们一年内的课外阅读量(单位：本)等数据，以下是根据数据绘制的统计图表的一部分．
下面有四个推断：
①这200名学生阅读量的平均数可能是26本；
②这200名学生阅读量的75％分位数在区间[30,40)内；
③这200名学生中的初中生阅读量的中位数一定在区间[20,30)内；
④这200名学生中的初中生阅读量的25％分位数可能在区间[20,30)内．所有合理推断的序号是 ．
15.若一组数据m，n，9，8，10的平均数为9，方差为2，则m−n= ．
16.已知样本数据a1､a2､a3､a4､a5都为正数，其方差s2=15a12+a22+a32+a42+a52−80，则样本数据2a1+3、2a2+3、2a3+3、2a4+3、2a5+3的平均数为_____．
四、解答题：本题共4小题，共48分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题12分)
某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛.为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分取正整数，满分为100分)作为样本进行统计.请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题：
频率分布表：
频率分布直方图：
(1)写出a，b，x，y的值;
(2)若根据这次成绩，学校准备淘汰90%的同学，仅留10%的同学进入下一轮竞赛，请问晋级分数线划为多少合理?
(3)某老师在此次考试成绩中抽取了10名学生的分数：x1，x2，x3，⋯，x10，已知这10个分数的平均数x=90，标准差s=6，若剔除其中的100和80两个分数，求剩余8个分数的平均数与标准差．
18.(本小题12分)
某市工会组织举行“红心向党”职工歌咏比赛，分初赛、复赛和决赛三个环节，初赛全市职工踊跃参与，通过各单位的初选，最终有2000名选手进入复赛，经统计，其年龄的频率分布直方图如图所示．
(1)求直方图中x的值，并估计复赛选手年龄的平均值(同一组中的数据用该区间的中点值作代表，结果保留一位小数)；
(2)根据频率分布直方图估计复赛选手年龄的第75百分位数；
(3)决赛由8名专业评审、10名媒体评审和12名大众评审分别打分，打分均采用10分制．已知某选手专业得分的平均数和方差分别为x1=8.4，S12=0.015，媒体得分的平均数和方差分别为x2=8.8，S22=0.054，大众得分的平均数和方差分别为x3=9.4，S32=0.064，将这30名评审的平均分作为最终得分，请估计该选手的最终得分和方差(结果保留三位小数)．
附：方差S2=1ni=1n(xi−x)2=1ni=1nxi2−x2．
19.(本小题12分)
从全校高二级部所有参加数学联赛的学生中抽取一个样本，考察联赛的成绩分布，将样本分成5组，绘制成频率分布直方图，图中从左到右各组的小长方形的高之比为3: 4 : 6: 5: 2，最右边一组的频数是6，请结合直方图提供的信息，解答下列问题：
(1)样本的容量是多少?
(2)列出频率分布表；
(3)估计这次联赛中全体学生的平均成绩和第75百分位数．
20.(本小题12分)
某超市从2018年甲、乙两种酸奶的日销售量(单位：箱)的数据中分别随机抽取100个，整理得到数据分组及频率分布
(1)写出频率分布直方图中的a的值，并作出甲种酸奶日销售量的频率分布直方图；
(2)记甲种酸奶与乙种酸奶日销售量(单位：箱)的方差分别为s12，s22，试比较s12与s22的大小；(只需写出结论)
(3)假设同一组中的每个数据可用该组区间的中点值代替，试估计乙种酸奶在未来一个月(按30天计算)的销售总量．
答案和解析
1.【答案】C
【解析】【分析】
本题考查统计图表等基础知识，属基础题．
直接根据统计图表逐项分析即可得到结论．
【解答】
解：根据统计图表可知，
这10天学生在线学习人数在逐日增加，但是增长比例并不是逐日增大项，故C项正确;A项错误;
前5天在线学习人数的比较稳定，后5天在线学习人数的波动较大，所以前5天在线学习人数的方差小于后5天在线学习人数的方差，B项错误;
前5天在线学习人数的增长比例的极差小于后5天的在线学习人数的增长比例的极差，D项错误．
故选C．
2.【答案】B
【解析】【分析】
本题考查折线图的应用，考查极差，平均数，百分位数和方差的应用问题，属于基础题．
由图分别计算出两组数据的百分位数，中位数，极差，平均数和方差再判断即可．
【解答】
解：对于A，甲成绩比较集中，乙成绩比较分散，所以甲成绩的极差小于乙成绩的极差，故A正确；
对于B，因为6×25％=1.5，所以成绩从小到大排序，甲的第25百分位数是第2位，乙的中位数在30到60，60到90，这两个成绩的平均数，由图可知甲的第2位明显大于乙的中位数，故B错误；
对于C，由统计图可知甲成绩的平均数大于乙成绩的平均数，故C正确；
对于D，甲成绩比较集中，乙成绩比较分散，所以甲成绩的方差小于乙成绩的方差，故D正确．
3.【答案】B
【解析】【分析】
本题考查了频率分布直方图的性质，属于基础题．
根据频率分布直方图的性质各项计算即可．
【解答】解：由频率分布直方图可知(a+0.015+0.035+b+a)×10=1，即b+2a=0.05，又b=3a，所以a=0.01，所以选项A正确;
满意度计分的众数为75分，所以选项B不正确;
前三组的频率之和为0.1+0.15+0.35=0.6<0.75，前四组的频率之和为0.6+0.3=0.9>0.75，则75%分位数m∈[80,90)，且m=80+0.75−0.60.9−0.6×10=85，满意度计分的75%分位数为85，所以选项C正确;
满意度计分的平均分为：x=55×0.1+65×0.15+75×0.35+85×0.3+95×0.1=76.5分，所以选项D正确．
故选B．
4.【答案】B
【解析】【分析】本题主要考查样本与总体的数字特征的基本知识，属于基础题．
根据题意，由方差、百分位数、平均数以及中位数的定义，分别代入计算，即可得到结果．
【解答】解：将样本数据从小到大排列为25，26，27，28，28，30，33，36，37，40，这10个月的月销售量的中位数为28+302=29，A错误;
这10个月的月销售量的平均数为25+26+27+⋯+37+4010=31，B正确;
根据百分位数的定义可知10×75%=7.5，则这10个月的月销售量的第75百分位数为第8个数36，C错误;
由图形可知，前5个月的月销售量的波动小于后5个月的月销售量的波动，所以前5个月的月销售量的方差小于后5个月的月销售量的方差，D错误，
故选B．
5.【答案】D
【解析】【分析】
本题主要考查的是中位数、平均数、标准差、百分位数，属于基础题；
根据中位数、平均数、标准差、百分位数等知识对选项进行分析，从而确定正确答案．
【解答】
解：A选项，甲队的中位数是 16+202=18 ，乙队的中位数是 17+192=18 ，
两者相等，所以A选项错误．
B选项，甲队的平均数为 7+12+16+20+22+316=1086=18 ，
乙队的平均数为 8+9+17+19+27+286=1086=18 ，
两者相等，所以B选项错误．
C选项，甲队的标准差为：
7−182+12−182+16−182+20−182+22−182+31−1826= 1753 ，
乙队的标准差为：
8−182+9−182+17−182+19−182+27−182+28−1826= 1823 ，
所以甲队数据的标准差小于乙队数据的标准差，所以C选项错误．
D选项，乙队的数据为 8,9,17,19,27,28 ， 6×0.75=4.5 ，
所以乙队数据的第75百分位数为 27 ，D选项正确．
故选：D
6.【答案】B
【解析】【分析】
本题主要考查了中位数，平均数和方差的计算，属于基础题．
先将数6，4，3，6，3，8，8，3，1，8，按小到大的顺序排列，再根据中位数、平均数、方差、百分位数的定义逐项求解判断．
【解答】
解：将数6，4，3，6，3，8，8，3，1，8，按小到大的顺序排列为：1，3，3，3，4，6，6，8，8，8，
则这组数据的中位数为4+62=5，故A正确；
平均数为：1+3×3+4+2×6+3×810=5，故C正确；
则方差为110[(1−5)2+(3−5)2×3+(4−5)2+(6−5)2×2+(8−5)2×3]=5.8，故B错误；
因为共有10个数，且10×85％=8.5，
所以85%分位数为第9个数，即为8，故D正确．
7.【答案】D
【解析】略
8.【答案】C
【解析】【分析】
本题考查了统计图，频率分布直方图和极差、中位数，属于中档题．
利用毕业生期望行业分布图，结合频率分布直方图中极差的概念对①进行判断，再利用中位数的概念对②进行判断，再利用百分率的概念对③进行判断，从而得结论．
【解答】
解：由题可知，期望值最大的为25.1%，最小的为0.9%，
所以期望值极差为25.1％−0.9％=24.2％，因此①正确；
因为期望值的中位数为5.1％+6.3％2=5.7％，因此②不正确；
因为从图中可知希望从事金融业工作的期望值为8.1%，
所以100个大学毕业生大约有100×8.1％=8.1≈8(人)希望从事金融业工作，因此③正确，
综上所述：正确选项的个数有2个．
故选C．
9.【答案】AD
【解析】【分析】
本题考查频率分布柱形图，折线图，考查极差、方差、平均数与百分位数的概念与计算，属于中档题．
根据柱形图中数据可估计症状感染者的极差，从而判断A；根据确诊病例数与无症状感染者数波动性的波动性判断B；直接计算平均数判断C；求出实际新增感染者的第80百分位数判断D．
【解答】
解：对于A，症状感染者的极差>800−300=500>400，A正确；
对于B，相比较而言，确诊病例数比无症状感染者数波动性小，所以确诊病例的方差小于无症状感染者的方差，B错误；
对于C，实际新增感染者的平均数
x=839+641+836+553+480+427+299+389+260+353+277+288+387+56814
≈471，
所以C错误；
对于D，因为14天内31省区市的实际新增感染者数从小到大分别为：260，277，288，299，353，387，389，427，480，553，568，641，836，839．
又14×80％=11.2，不是整数，
所以实际新增感染者的第80百分位数为为第12位，即为641，所以D正确．
10.【答案】BC
【解析】【分析】
本题考查频率分布直方图中中位数、平均数、百分位数以及方差的求法，考查数学运算能力，属于中档题．
根据频率分布直方图计算出中位数、平均数、百分位数以及方差，即可判断正确选项．
【解答】
解：根据频率分布直方图可得骑车时间为22分时的频率为0.6不是0.5，
所以中位数估计值不是22分钟，所以A错；
根据频率分布直方图可得坐公交车时间的40%分位数的估计值是18+202=19分钟，所以B对；
根据频率分布直方图可得坐公交车时间、骑车时间平均数的估计值分别为(13+27)×0.05+(15+25)×0.1+(17+23)×0.15+(19+21)×0.2=2+4+6+8=20、19×0.2+21×0.4+23×0.3+25×0.1=21.6>20，所以C对．
坐公交车时间的平均数的估计值为：20，
则方差s12=(13−20)2×0.05+(15−20)2×0.1+(17−20)2×0.15
+(19−20)2×0.2+(21−20)2×0.2
+(23−20)2×0.15+(25−20)2×0.1+(27−20)2×0.05=13；
骑车时间的平均数的估计值为：21.6，
则方差s 22=(19−21.6)2×0.2+(21−21.6)2×0.4
+(23−21.6)2×0.3+(25−21.6)2×0.1=3.24，
故坐公交车时间的方差估计值大于骑车时间的方差的估计值，故D错误．
故选：BC．
11.【答案】ACD
【解析】略
12.【答案】B
【解析】【分析】
本题考查信息的读取与分析能力，考查学生根据所给信息进行推断能力，属于中档题．
根据图中信息结合选项逐一判断正误即可得出结果．
【解答】
解：由扇形图可判断54周岁以上所占比例最少，故参保人数最少，A选项正确；
由折线图可估计18∼29周岁人均参保费用最少，但所占比例为20%，
∴总费用不是最少，故B选项错误；
由条形图可知丁险种的参保比例更高，可判断C选项正确；
由扇形图可知30周岁以上所占比例为1−20%=80%，故D选项正确．
故选B．
13.【答案】n【解析】【分析】
本题考查了统计中的基本统计量，中位数、众数、平均数的计算，是基础题．
由统计图依次求出中位数，众数，平均数，即可得到结果．
【解答】
解：由统计图得，得分值的中位数为m=5+62=5.5，
众数为n=5，
平均数为x=130(3×2+4×3+5×10+6×6+7×3+8×2+9×2+10×2)≈5.97，
∴n故答案为n14.【答案】②③④
【解析】【分析】
本题考查命题真假的判断，考查频率分布直方图、平均数、75%分位数、中位数、25%分位数等基础知识，考查运算求解能力，是中档题．
利用频率分布直方图、平均数、75%分位数、中位数、25%分位数直接求解．
【解答】
解：在①中，由学生类别阅读量中男生和女生人均阅读量知，这200名学生的平均阅读量在区间(24.5,25.5)内，故①错误；
在②中，200×75%=150，
阅读量在[0,30)中有：15+60+51=126名学生，阅读量在[30,40)中有62名学生，
∴这200名学生阅读量的75%分位数在区间[30,40)内，故②正确；
在③中，设在区间[0,10)内的初中生人数为x，则x∈[0,15]，x∈N，
当x=0时，初中生总人数为116人，116×50%=58，
此时，区间[0,20)有25人，区间[20,30)有36人，所以中位数在区间[20,30)内；
当x=15时，初中生总人数为131人，131×50%=65.5，
此时，区间[0,20)有15+25=40人，区间[20,30)有36人，所以中位数在区间[20,30)内；
所以，当x∈[0,15]，x∈N时，中位数都在区间[20,30)内；
综上，这200名学生中初中生阅读量的中位数一定在区间[20,30)内，故③正确；
在④中，设在区间[0,10)内的初中生人数为x，则x∈[0,15]，x∈N，
当x=0时，初中生总人数为116人，116×25%=29，
此时，区间[0,20)有25人，区间[20,30)有36人，所以25%分位数在区间[20,30)内；
当x=15时，初中生总人数为131人，131×25%=32.75，
此时，区间[0,20)有15+25=40人，所以25%分位数在区间[0,20)内；
所以，这200名学生中初中生阅读量的中位数可能在区间[20,30)内，故④正确；
故答案为：②③④．
15.【答案】4
【解析】【分析】
本题考查平均数，方差，属于基础题．
根据平均数，方差的公式列出方程求解即可．
【解答】
解：根据题意得平均数 x=15m+n+9+8+10=9 ，
方差 s2=15m−92+n−92+9−92+8−92+10−92=2 ，
所以 m+n=18 ，且 m−92+n−92=8 ，解得 n=11,m=7 或 n=7,m=11,
所以 m−n=4 ．
故答案为：4．
16.【答案】11
【解析】【分析】
本题考查平均数的求法，解题时要认真审题，注意平均数、方差的性质的合理运用，属于中档题．
设样本数据a1、a2、a3、a4、a5的平均数为x，推导出5x2=80，解得x，由此能求出2a1+3，2a2+3，2a3+3，2a4+3，2a5+3的平均数．
【解答】
解：根据题意，设样本数据a1、a2、a3、a4、a5的平均数为x，
其方差s2=15a1−x2+a2−x2+a3−x2+a4−x2+a5−x2
=15a12+a 22+a 32+a 42+a 52−2a1x−2a2x−2a3x−2a4x−2a5x+5x 2
=15(a 12+a 22+a 32+a 42+a 52−5x2)，
又s2=15a12+a 22+a 32+a 42+a 52−80，则有5x2=80，解得x=4，
则样本数据2a1+3、2a2+3、2a3+3、2a4+3、2a5+3的平均数为2x+3=11．
故答案为：11．
17.【答案】解：(1)设样本容量为N，则N=200.40=50，
所以第4组的频数为50×0.08=4，
则a=50−8−20−4−2=16，b=250=0.04，x=165010=0.032，y=0.0410=0.004；
(2)[50,60)、[60,70)、[70,80)、[80,90)的频率分别为0.16，0.32，0.40，0.08，
且0.16+0.32+0.40=0.88，0.16+0.32+0.40+0.08=0.96，
设晋级分数线划为x分，则x−80×0.008=0.9−0.88，解得x=82.5，
故晋级分数线划为82.5分；
(3)由题意，剩余8个分数的平均值为x0=10x−100−808=90，
因为10个分数的标准差s= i=110xi2−10×90210=6，
所以x12+⋯+x102=10×62+10×902=81360．
所以剩余8个分数的标准差为s0= x12+⋯+x102−802−1002−8×9028= 20=2 5．
【解析】本题考查了频率分布表与频率分布直方图，考查了百分位数，考查了平均数与标准差，属于中档题．
(1)利用频率=(频数÷样本容量)×100%，及频数÷组距表示频率分布直方图的纵坐标即可求出a，b，x，y；
(2)得到各组的频率，根据百分位数的概念即可求解；
(3)根据平均数与标准差的定义求解即可．
18.【答案】解：(1)由频率分布直方图知，(0.01+0.015+0.020+2x+0.030+0.035+0.040)×5=1，
解得x=0.025，
因此复赛选手年龄的平均值x=(22.5×0.010+27.5×0.025+32.5×0.035+37.5×0.040+42.5×0.030+47.5×0.025+52.5×0.020+57.5×0.015)×5
≈39.6(岁)．
(2)因为(0.010+0.025+0.035+0.040+0.030)×5=0.7<0.75，
所以第75百分位数落在[45,50)区间内，设为t，
则(0.010+0.025+0.035+0.040+0.030)×5+(t−45)×0.025=0.75，
解得t=47，即第75百分位数为47分．
(3)由S2=1ni=1n(xi−x)2 ，
设该名选手最终的平均分为y，最终方差为s2，
则y=18+10+12(8.4×8+8.8×10+9.4×12)≈8.933(分)，
s2=130{8[S12+(x1−y)2]+10[S22+(x2−y)2]+12[S32+(x3−y)2]}
=130{8[0.015+(8.4−8.933)2]+10[0.054+(8.8−8.933)2]
+12[0.064+(9.4−8.933)2]}
≈0.216．
估计该选手最终得分为8.933分，其得分方差为0.216．
【解析】本题考查了频率分布直方图的应用，考查平均数和方差以及百分位数的计算，属于中档题．
(1)利用频率分布直方图频率之和为1求得x=0.025，再利用频率分布直方图，计算平均值得结论；
(2)利用频率分布直方图，结合第75百分位数的概念，计算得结论；
(3)利用平均数和方差的计算公式，计算得结论．
19.【答案】解：(1)由题意，频率之比为3: 4 : 6: 5: 2，最右边一组的频数是6，
所以样本容量为6÷23+4+6+5+2=60，
(2)由(1)知样本容量为60，所以从左到右的频数分别为9，12，18，15，6;
故频率分别为0.15,0.2,0.3,0.25,0.1;
故频率分布表为：
(3)平均成绩为55×0.15+65×0.2+75×0.3+85×0.25+95×0.1=74.5，
因为0.75∈0.65,0.9，所以第75百分位数位于80,90内，即80+0.75−×10=84，
故第75百分位数是84分．
【解析】本题考查频率直方图，频率分布表，平均数和用样本估计百分位数，属于中档题．
(1)根据最右边一组的频数是6，而频率等于该组的面积在整个图形面积中的百分比，因此可得样本容量为60；
(2)依据样本容量为60和各组比例，可计算频率和频数，画出表格即可；
(3)根据频率分布直方图计算平均数和第75百分位数即可．
20.【答案】解：(1)a=0.015
(2)s12(3)乙种酸奶平均日销售量为：
x=5×0.20+15×0.10+25×0.30+35×0.15+45×0.25=26.5(箱)，
乙种酸奶未来一个月的销售总量为26.5×30=795(箱)．

【解析】本题考查频率分布直方图的认识，属于中档题．
(1)利用频率总和为1求出a的值；
(2)根据频率分布直方图的数据分布情况可知波动大的方差也大；
(3)求出乙种酸奶平均日销售量即可求解．阅读量
人数
学生类别
[0,10)
[10,20)
[20,30)
[30,40)
[40,+∞)
性别
男
7
31
25
30
4
女
8
29
26
32
8
学段
初中
25
36
44
11
高中
组别
分组
频数
频率
第1组
[50,60)
8
0.16
第2组
[60,70)
a
■
第3组
[70,80)
20
0.40
第4组
[80,90)
■
0.08
第5组
[90,100]
2
b
第6组
合计
■
■
分组(日销售量)
频率(甲种酸奶)
[0,10]
0.10
(10,20]
0.20
(20,30]
0.30
(30,40]
0.25
(40,50]
0.15
成绩
50,60
60,70
70,80
80,90
90,100
频数
9
12
18
15
6
频率
0.15
0.2
0.3
0.25
0.1