299，江苏省苏州市姑苏区苏州中学校2023-2024学年九年级上学期10月月考数学试题

这是一份299，江苏省苏州市姑苏区苏州中学校2023-2024学年九年级上学期10月月考数学试题，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．下列函数的解析式中，一定为二次函数的是（ ）
A．B．
C．D．（是常数）
2．对于抛物线，下列说法正确的是（ ）
A．抛物线开口向上B．当时，随的增大而减小
C．函数最小值为D．顶点坐标为
3．抛物线的对称轴是直线（ ）
A．B．C．D．
4．若二次函数，当取时，函数值相等，则当取时，函数值为（ ）
A．B．C．D．
5．已知点，，在函数的图象上，则的大小关系是（ ）
A．B．C．D．
6．函数的图象如图所示，那么关于的一元二次方程的根的情况是（ ）
A．有两个不相等的实数根B．有两个异号的实数根
C．有两个相等的实数根D．没有实数根
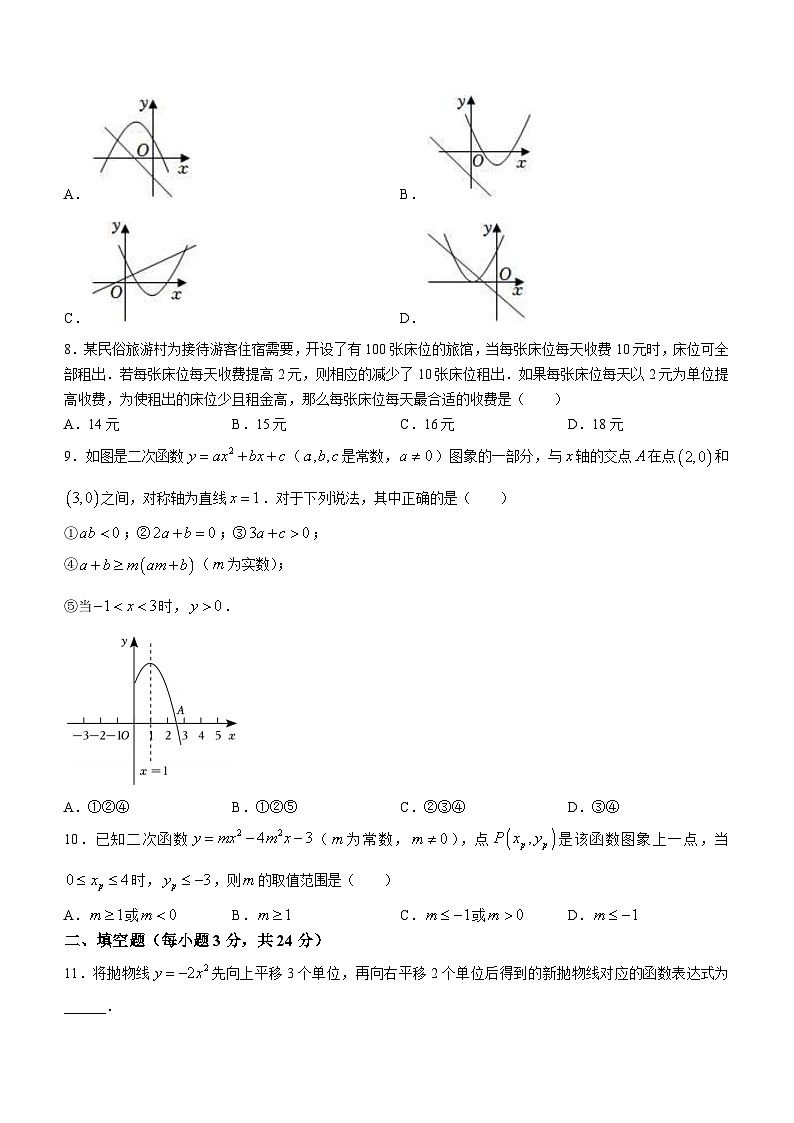
7．在同一直角坐标系中，函数和（是常数，且）的图象可能是（ ）
A．B．
C．D．
8．某民俗旅游村为接待游客住宿需要，开设了有100张床位的旅馆，当每张床位每天收费10元时，床位可全部租出．若每张床位每天收费提高2元，则相应的减少了10张床位租出．如果每张床位每天以2元为单位提高收费，为使租出的床位少且租金高，那么每张床位每天最合适的收费是（ ）
A．14元B．15元C．16元D．18元
9．如图是二次函数（是常数，）图象的一部分，与轴的交点在点和之间，对称轴为直线．对于下列说法，其中正确的是（ ）
①；②；③；
④（为实数）；
⑤当时，．
A．①②④B．①②⑤C．②③④D．③④
10．已知二次函数（为常数，），点是该函数图象上一点，当时，，则的取值范围是（ ）
A．或B．C．或D．
二、填空题（每小题3分，共24分）
11．将抛物线先向上平移3个单位，再向右平移2个单位后得到的新抛物线对应的函数表达式为______．
12．已知抛物线的顶点在轴上，则的值为______．
13．已知二次函数的图象上，当时，随的增大而增大，则的取值范围是______．
14．初三数学课本上，用“描点法”画二次函数的图象时，列了如下表格：
根据表格上的信息回答问题：该二次函数在时，______．
15．对于任何的实数，抛物线总经过一个固定的点，这个点坐标是______．
16．抛物线的对称轴为直线，若关于的一元二次方程（为实数）在的范围内有实数根，则的取值范围是______．
17．已知实数满足，则代数式的最小值等于______．
18．在平面直角坐标系中，一个图形上的点都在一边平行于轴的矩形内部（包括边界），这些矩形中面积最小的矩形称为该图形的关联矩形．例如：如图，函数的图象（抛物线中的实线部分），它的关联矩形为矩形．若二次函数图象的关联矩形恰好也是矩形，则______．
三、解答题（共76分）
19．在直角坐标平面内，二次函数图象的顶点为，且过点．
（1）求该二次函数的解析式；
（2）当时，求出的取值范围．
20．如图，直线和抛物线都经过点．
（1）求的值和抛物线的解析式；
（2）求不等式的解集．（直接写出答案）
21．如图，隧道的截面由抛物线和长方形构成，长方形的长为，宽为，抛物线的最高点离地面的距离为．
（1）按如图所示的直角坐标系，求表示该抛物线的函数表达式．
（2）一大型汽车装载某大型设备后，高为，宽为，如果该隧道内设双向行车道，那么这辆货车能否安全通过？
22．某超市销售一种商品，成本价为50元/千克，规定每千克售价不低于成本价，且不高于85元经市场调查，该商品每天的销售量（千克）与售价（元/千克）满足一次函数关系，部分数据如表：
（1）求与之间的函数表达式．
（2）设该商品每天的总利润为（元），则当售价定为多少元/千克时，超市每天能获得最大利润？最大利润是多少元？
（3）如果超市要获得每天不低于1600元的利润，且符合超市自己的规定，那么该商品的售价的取值范围是多少？请说明理由．
23．如图，已知抛物线与一直线相交于两点，与轴交于点．其顶点为．
（1）抛物线及直线的函数关系式；
（2）设点时对称轴上的一点，求使的值最小时的的坐标；
（3）若是抛物线上位于直线上方的一个动点，求的面积的最大值．
24．在平面直角坐标系中，对于点，如果将其坐标作如下变换；，进而得到，则称为点的“对称点”。例如：点的“变换点”是点的变换点是点，点的“变换点”是．
（1）点的变换点的坐标是______；
（2）若抛物线上存在点的“变换点”，求的取值范围．
25．已知，如图，抛物线的顶点为，经过抛物线上的两点和的直线交抛物线的对称轴于点．
备用图
（1）求抛物线的解析式和直线的解析式．
（2）若点在抛物线上，点在轴上，当以点为顶点的四边形是平行四边形时，直接写出满足条件的点的坐标．
（3）将直线向上平移5个单位后与抛物线交于点（对应点对应点），在直线下方的抛物线上有一点E，满足，求点E的坐标．
26．如图，抛物线与坐标轴分别交于三点，是第一象限内抛物线上的一点且横坐标为．
（1）三点的坐标______，______，______；
（2）连接，交线段于点．
①当CP与轴平行时，求的值
②当CP与轴不平行时，连接CP、AD，求的最大值
③连接，是否存在点，使得，若存在，求的值，若不存在，请说明理由．
2023-2024学年苏州中学园区校初三年级10月份月考数学试卷
参考答案与解析
一、选择题（每小题3分，共30分）
1．【答案】C
【解答】解：A．是一次函数，不是二次函数，故此选项错误；
B．，不是二次函数，故此选项错误；
C．是二次函数，故此选项正确；
D．当时是一次函数，不是二次函数，故此选项错误．
故选：C．
2．【答案】B
【解答】解：的二次项系数为，抛物线开口向下，故A不符合题意．
抛物线开口向下，对称轴，当时，随的增大而减小．故B符合题意．
当时，取最大值，故C不符合题意．
抛物线的顶点坐标为，故D不符合题意．
故选：B．
3．【答案】A
【解答】解：是方程的两根，
抛物线与轴交点横坐标是，
这两个点关于对称轴对称，对称轴是直线．
故选：A．
4．【答案】D
【解答】解：抛物线对称轴为轴
互为相反数
所以当取时， 故选：D．
5．【解答】解：点在函数的图象上，
点都满足函数解析式，，，，．
故选：A．
6．【答案】D
【解答】解：一元二次方程的根可以看成和的交点，从图象看，上述两个函数的无交点，
故一元二次方程的根为：没有实数根．
故选D．
7．【答案】D
【解答】解：A．由函数的图象可知，即函数开口方向朝上，与图象不符，故A选项错误；
B．由函数的图象可知，即函数开口方向朝上，称轴为，则对称轴应在轴左侧与图象不符，故B选项错误；
C．由函数的图象可知，即函数开口方向朝下，故C选项错误；
D．由函数的图象可知，即函数开口方向朝上，对称轴为，则对称轴应在轴左侧，与图象相符，故D选项正确．
故选：D．
8．【解答】解：设每张床位提高个2元，每天收入为元．
则有．
当时，可使有最大值．
又为整数，则时，；
时，；
则为使租出的床位少且租金高，每张床收费（元）．
故选：C．
9．【答案】A
【解答】解：由函数图象可知，抛物线开口向下，，
抛物线的对称轴为直线，，，故①正确；
，，故②正确；
由可将函数解析式变形为，
抛物线的对称轴为直线，
当和时，所对应的函数值相同，
由图可知，当时，，
当时，，即，故③错误；
抛物线的开口向下，对称轴为直线，当时，取得最大值，
（为实数），
整理得：，故④正确；
与轴的交点在点和之间
可设点的坐标为，则抛物线与轴的另一交点坐标为，
当，时，，故⑤错误．
综上，正确的有①②④．
故选：A．
10．【答案】A
【解答】解：二次函数，
对称轴为，抛物线与轴的交点为，
点是该函数图象上一点，当时，，
①当时，对称轴，
此时，当时，，即，解得；
②当时，对称轴，
当时，随增大而减小，则当时，恒成立；
综上，的取值范围是：或．
故选：A．
二、填空题（每小题3分，共24分）
11．．
【解答】解：将抛物线的图象先向上平移3个单位，再向右平移2个单位，得到新的抛物线解析式为：．
故答案为：．
12．．
【解答】解：抛物线的顶点在轴上，
，即，解得．
故答案为：．
13．．
【解答】解：二次函数的对称轴为直线，
当时，的值随值的增大而增大，．
故答案为：．
14．．
【解答】解：观察表格可知，当或2时，，
根据二次函数图象的对称性，
是抛物线上两对称点，
对称轴为，顶点，
根据对称性，与时，函数值相等，都是．
故答案为：．
15．．
【解答】解：，
当，即时，的值与无关，，
所以，抛物线总经过一个固定的点．
故答案为：．
16．．
【解答】解：抛物线的对称轴为直线，
，得，，
当时，的取值范围是，
当时，，即，
关于的一元二次方程（为实数）在的范围内有实数根，
的取值范围是，
故答案为：．
17．11．
【解答】解：，，
则原式化为：，
，
代数式的最小值等于，
故答案为：11．
18．【答案】或．
【解答】解：由，当时，，，
，四边形是矩形，，
①当抛物线经过时，将点代入得
，解得；
②当抛物线经过时，将点代入得
，解得，
综上所述，或，
故答案为：或，
19．【解答】解：（1）二次函数图象的顶点为，
设二次函数解析式为，
把点代入二次函数解析式，得：，解得，
二次函数解析式为，即；
（2），二次函数的对称轴为，二次函数开口向上
当时，，当时，
则的取值范围为．
三、解答题（共76分）
20．【解答】解：（1）把点分别代入直线和抛物线得：
，，，
所以；
（2），解得：或．
21．【解答】解：（1）根据题意得，
设抛物线的解析式为，把代入
解得：．抛物线的解析式为．
（2）根据题意，把代入解析式，得．
，货运卡车能通过．
22．【解答】解：（1）设，
将代入，得：，解得：，
；
（2），
当时，取得最大值为1800元，
答：售价为80元时获得最大利润，最大利润是1800元．
（3）当时，得：，
解得：或，
该抛物线的开口向下，当时，，
又每千克售价不低于成本，且不高于85元，即，
该商品每千克售价的取值范围是．
23．【解答】解：（1）由抛物线过点及得，，
解得，故抛物线为
又设直线为过点及得，解得
故直线为；
（2）点坐标为，作点关于直线的对称点，则，
由对称知识得，则，当点，点，点点三点共线时，的值最小，此时
设过的直线为
则点坐标为
（3）方法一：如图3，过点作轴交于点，交轴于点；过点作轴于点，设，则
又
面积的最大值为．
方法二：过点作轴交于点，交轴于点；过点作轴于点，如图3，设，则
又
的面积的最大值为．
图3
24．【解答】（1）
（2）当时，由得
若此时二次函数的图象上存在点的变换点
则 ．
解得或；（不合题意，舍去）．
当时，由得．
若此时二次函数的图象上存在点的变换点
则．
解得或（不合题意，舍去）
综上，或
25．【解答】解：（1）二次函数表达式为：，
将点的坐标代入上式并解得：，
故抛物线的表达式为：，则点，
将点的坐标代入一次函数表达式并解得：
直线的表达式为：；
（2）设点、点，
①当是平行四边形的一条边时，
点向左平移4个单位向下平移16个单位得到，
同理，点向左平移4个单位向下平移16个单位为，即为点，
即：，，而，解得：或，
故点或；
②当是平行四边形的对角线时，
由中点公式得：，而，解得：，
故点或；
综上，点或或或．
（3）将线段绕着点逆时针旋转得到点，则直线与抛物线的交点即为点
则，，则点坐标为
26．【答案】（1）；
（2）；（3）存在，．
【解答】解：（1）当时，，，
当时，可得方程，解得或，
．
（2）①当与轴平行时，求的值
当与轴平行时，
则当，，则
②如图，过点作的平行线，交于点，
，，，
，，
设的解析式为，将代入解析式，得，解得，
的解析式为，故可得，
，
当时，取最大值为．
（3）假设存在点，如图，延长交轴于点，过点作的垂线，交抛物线于点，
，，，，
，，
，，
，，
设的解析式为，将代入解析式得：，
解得：，解析式为，
令，解得或（舍），
存在点满足题意，此时．…
0
1
2
…
…
…
售价（元/千克）
50
60
70
销售量（千克）
120
100
80