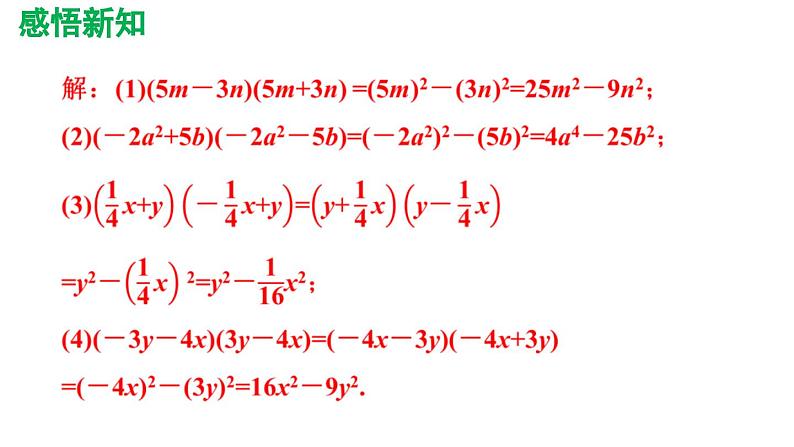
北师大版5 平方差公式多媒体教学课件ppt

这是一份北师大版5 平方差公式多媒体教学课件ppt，共23页。PPT课件主要包含了逐点学练，本节小结，作业提升，本节要点，学习流程，知识点，平方差公式，平方差公式的验证，结构特征，运用公式计算等内容，欢迎下载使用。

平方差公式平方差公式的验证
1. 平方差公式两数和与这两数差的积，等于它们的平方差.即：用字母表示为(a+b)(a－b)=a2－b2.
特别解读公式的特征：1. 等号左边是两个二项式相乘，这两个二项式中有一项完全相同，另一项互为相反数.2. 等号右边是乘式中两项的平方差，即相同项的平方减去相反项的平方.3. 理解字母a，b 的意义，平方差公式中的a，b既可代表一个单项式，也可代表一个多项式.
2. 平方差公式的几种常见变化及应用
解题秘方：先确定公式中的“a”和“b”，然后根据平方差公式(a+b)(a－b)=a2－b2 进行计算.
1-1. 若(2－x)(2+x)(4+x2)=16－xn， 则n的值等于( )A. 6 B. 4C. 3 D. 2
1-2. 若(2x+3y)(mxny)=9y2－4x2， 则( )A. m=2， n=3B. m=－2， n=－3C. m=2， n=－3D. m=－2， n=3
1-3. 计算：(1)(2a－3b)(2a+3b)；(2)(－2a－1)(－1+2a)；
解：原式＝(2a)2－(3b)2＝4a2－9b2；
原式＝(－1－2a)(－1＋ 2a) ＝ (－ 1)2－(2a)2 ＝1－4a2；
原式＝1－a2 ＋a2 －2a ＝1－2a.
计算：(1)10.3×9.7；(2)2 022×2 024－2 0232.
解题秘方：找出平方差公式的模型，利用平方差公式进行计算.
解：(1)10.3×9.7=(10+0.3)×(10－0.3)=102－0.32=100－0.09=99.91；
10.3 与9.7 的平均数为10
(2)2 022×2 024－2 0232=(2 023－1)×(2 023+1)－2 0232=2 0232－12－2 0232=－1.
2 022 与2 024 的平均数为2 023
2-1. 运用平方差公式进行简便计算：(1)9.8×10.2；
解：原式＝ (10－0.2) ×(10＋0.2) ＝102 －0.22＝100 －0.04＝99.96；
原式＝ (128＋1) × (128－1) －1282＝1282 －12 －1282 ＝ －1.
平方差公式的几何意义如图1-5-1 ①，边长为a 的大正方形中有一个边长为b 的小正方形，则图中阴影部分的面积是a2－b2; 将图1-5-1 ①中的阴影部分剪拼成一个长方形，如图1-5-1 ②，这个长方形的长为a+b，宽为a－b，面积为(a+b)(a－b).因为图1-5-1 ①和图1-5-1 ②中阴影部分的面积相等, 所以(a+b)(a－b)=a2－b2.
特别提醒利用图形验证平方差公式的关键是将同一个图形的面积用不同的方法表示, 即直接表示和间接表示.
如图1-5-2 ① , 在边长为a 的正方形中, 剪去一个边长为b 的小正方形(a﹥b)后, 将余下部分按图中虚线剪开，然后拼成一个梯形如图1-5-2 ②所示, 通过计算两个图形中阴影部分的面积, 可以验证公式__________________ .
a2－b2=(a+b)(a－b)
解题秘方：紧扣面积法，用不同方法表示两个图形中阴影部分的面积, 利用面积相等验证公式.
3-1. 从边长为a 的正方形中剪掉一个边长为b 的正方形(如图①)，然后将剩余部分拼成一个长方形(如图②).上述操作能验证的等式是( )(请选择正确的一个)A. a2－2ab+b2=(a－b)2B. a2－b2=(a+b)(a－b)C. a2+ab=a(a+b)